CDB Loss - 논문리뷰

클래스 불균형을 해결하기 위해 클래스 난이도에 따라 동적으로 loss 가중치를 할당하는 방법인 Class-wise Difficulty-Balanced Loss에 대해 논문을 알아보겠습니다.

Introduce

사람들이 학습을 하기 위해 만든 데이터 셋은 클래스의 분포가 일정한 경우가 많습니다. 그러나 현실의 데이터(long tails)들은 각 클래스의 데이터 수가 다 다릅니다.(논문에서 수가 많지만 클래스 갯수가 적은 클래스들을 majority classes, 수가 적지만 클래스 갯수가 많은 클래스들은 minority classes로 부릅니다)

이전에 해온 연구에는 re-sampling, Metrix learning, knowledge transfer, Cost-sensitive learning methods가 있습니다. related works에서 이와 관련된 얘기를 더 자세히 하기 때문에 Introduce에서의 설명은 넘어가도록 하겠습니다.

논문의 key-point는 아래 두가지와 같습니다.
1. 동적으로 difficulty를 측정하고 훈련도중에 각 클래스에 사용해 re-balance합니다.
2. CDB loss는 이미지, 비디오 등 데이터 타입에 상관없이 잘 동작하고 클래스의 동적 난이도를 정량화 하고 이를 가중치에 사용하는 연구에 유용하게 사용될 수 있습니다.

Related Works

Data Re-sampling

Data re-sampling에는 over-sampling과 under-sampling 방법이 있습니다. majority sample은 under-sampling, minority sample은 over-sampling을 사용합니다. 각각의 단점으로 over-sampling는 중복되는 데이터가 생길 수 밖에 없어서 overfitting의 위험이 커지고, under-sampling는 중요한 데이터를 삭제할 가능성이 있다는 점입니다. over-sampling의 일종인 SMOTE(Synthetic Minority Over sampling Technique)같은 데이터 합성 방법은 중복 데이터가 아닌 새로운 데이터를 만들어냅니다. 그러나 이 역시 합성한 데이터가 실제 minority 클래스의 데이터 분포를 나타낸다고 보장할 수 없습니다.

Metric Learning and Knowledge Transfer

Metric Learning은 데이터 간의 관계가 잘 보존되는 특징 공간을 잘 임베딩(축소)하는 함수를 학습하는 것을 목적으로 합니다. Contrastive embedding은 같은 클래스의 데이터 특징의 거리는 최소화 할 수 있게 다른 클래스의 데이터 특징은 거리가 최대화 될 수 있게 학습합니다. Triplet loss는 하나를 앵커로 사용하여 세 개의 데이터 쌍을 쓰는 방법을 사용합니다. 그러나 Metric Learning은 여전히 majority classes에 편향되어 임베딩 될 가능성이 높습니다. 이를 해결하기 위해 OLTR이라는 방법이 나왔습니다. 이는 transfer learning으로 meta learning을 이용해 majority classes를 minority classes로 지식을 전수하는 방법입니다.(정확한 내용은 논문을 읽어봐야 알 것 같습니다.)
이 OLTR은 long-tail classfication에 대해 잘 동작했지만 비용적인 측면에서 오버헤드가 크다고 합니다.

Cost-Sensitive Learning

cost-sensitive learning은 예측이 틀린 클래스에 대해 더 높은 불이익(가중치)를 주는 방법을 뜻합니다. 대부분 클래스 불균형을 해결하기 위해 minority class에 더 큰 가중치를 주는 방법을 택합니다. Class Balanced lossd처럼 샘플의 수(정확히는 Effective Number)에 반비례하여 가중치를 부여하는 방법은 쉬운 데이터는 적은 데이터로도 충분히 학습할 수 있는 경우가 있기 때문에 잘못된 학습이 될 수 있습니다. 그런 점에서 Focal loss를 보면 어려운 데이터(loss가 높은 것)에 큰 가중치를 주는 방향으로 학습을 하는데 이는 minority class data가 hard sample이 높다는 가정을 하고 사용을 합니다(실제로도 높다고 하는데 이유가 뭔지 찾아봐야 할 것 같습니다.) 그러나 비율이 높다고 하더라고 절대적인 수 자체는 majority classes data가 훨씬 많기 때문에 클래스와 관계없이 어려운 데이터에 높은 가중치를 부여하면 majority class로 성능이 편향된다고 합니다.

Propsed Method

논문에서 제시하는 Class Difficulty를 구하는 방법은 아래의 수식과 같습니다.

각 클래스는 c로 나타내고 t는 학습한 에폭을 의미합니다. $A_{c}=n_c/N_c$ 이며 $N_c$, $n_c$는 각각 validation dataset에서 클래스 c의 전체 데이터 셋 수와 정답을 맞춘 데이터 수 입니다.

이제 난이도에 따른 가중치는 어떻게 구하는가?를 알아볼 차례입니다. 클래스 분류가 어려울 수록 가중치가 높아야 하는건 자명한 사실입니다.

$\tau$는 하이퍼파라미터입니다.
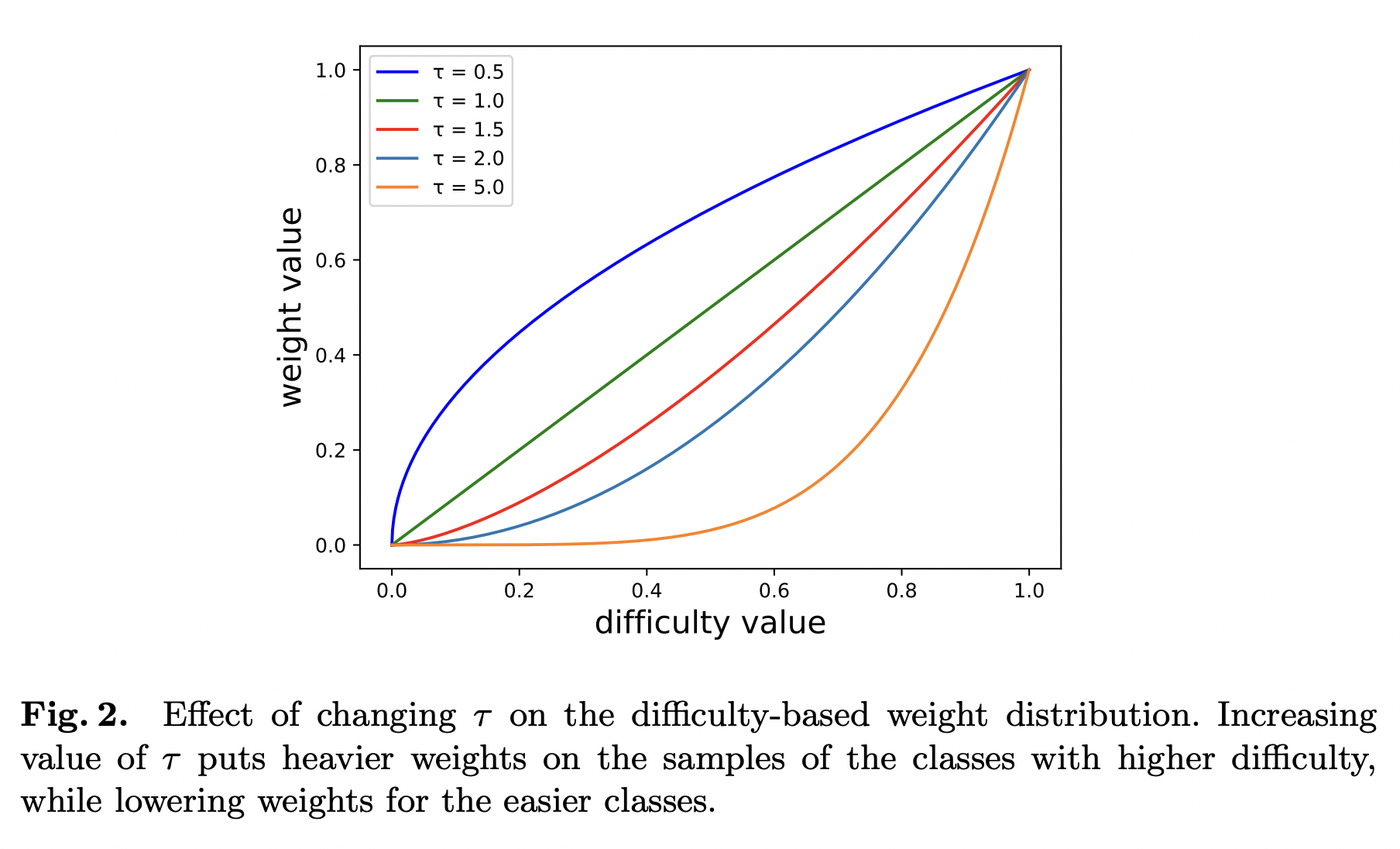위는 하이퍼 파라미터 $\tau$에 따라 쉬운 클래스와 어려운 클래스의 가중치를 얼마나 바뀌는지 볼 수 있는 그래프입니다.

best $\tau$는 데이터 셋마다 다르기 때문에 실험이 필요하다고 합니다. 논문에서는 이를 동적으로 하는 방법도 소개합니다.

분자가 2이면 1부터 2까지만 동적으로 조절할 수 있습니다.

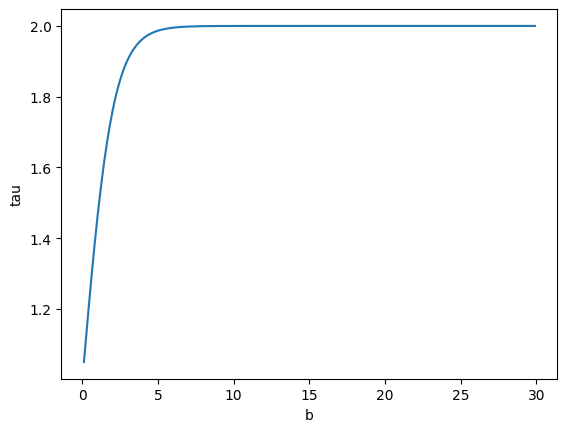
$b_t$는 가장 작은 accuracy 클래스에서 가장 큰 accuracy를 나누어 사용합니다. accuracy 차이가 많이나면 높은 편향을 가지고 있다는 의미로(high $b_t$) $\tau$를 높여 클래스간 가중치 차이가 많이 나도록 하고, accuracy 차이가 적으면 낮은 편향을 가지고 있다는 의미로 (low $b_t$) $\tau$를 낮춰 클래스간 가중치 차이가 적게 만듭니다. 간단한 아래 그래프의 b를 따라가면서 확인하면 이해하기 쉽습니다.

마지막으로 난이도를 결합해서 만든 CDB-CE loss를 보겠습니다. 식은 간단합니다.

Experiments

실험은 MNIST, CIFAR, ImageNet-LT, EGTEA 4개의 데이터셋에서 진행했습니다.(클래스 불균형은 인위적으로 만들어서 실험을 했습니다) 논문에서는 $\tau$에 대해 다양한 실험을 했습니다.
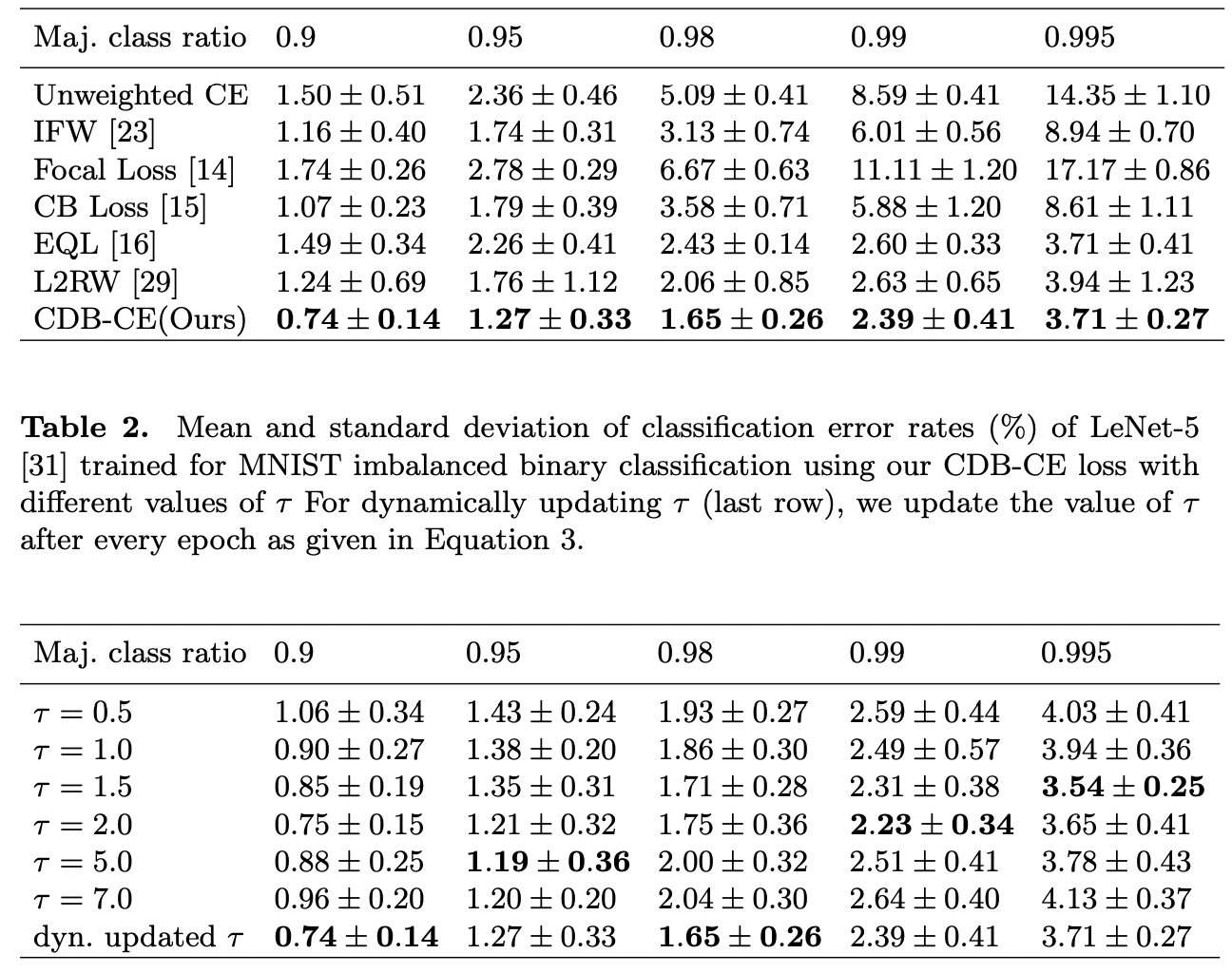위는 클래스 불균형 정도에 loss 성능과 $\tau$성능에 대한 테이블입니다.
모든 상황에서 동적 업데이트가 좋은 것은 아닙니다만 다른 loss들과 비교해서는 좋은성능을 내는 것을 볼 수 있습니다.(근데 분자를 더 크게 해서 $\tau$범위를 더 크게 했으면 성능이 어땠을지 궁금하네요)

이 외에도 다른 실험을 확인 하려면 논문에서 모두 확인할 수 있습니다. 평균적인 성능은 CDB loss가 가장 좋았습니다.
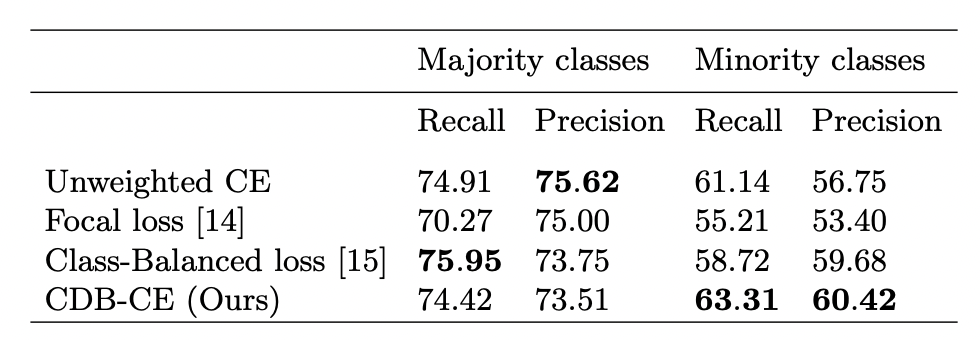논문에서는 이런 종류의 실험까지 했습니다. Majority class와 minority class의 Recall과 Precision이 어떤지 확인해볼 수 있습니다. 확실히 minoritiy classes를 더 구분 잘하는 것을 볼 수 있습니다.

Conclusion

이 논문에서는 새로운 weighted-loss 방법론을 제시했고 각 클래스마다 훈련의 샘플 수가 아닌 난이도를 고려하는 방법을 선택했습니다. 또한 동적 난이도를 정량화 하는 방법에 대해 얘기하며 데이터 타입에 관계없이 불균형 클래스 데이터셋에 대해 좋은 성능을 얻을 수 있습니다.

더 자세한 내용은 논문에서 확인할 수 있고 코드는 공식 깃허브 링크에서 확인 할 수 있습니다.