이번 assignment는 lecture1에서 배운 knn알고리즘을 실제로 구현해보고 실제로 k값을 조절 해보면서 최적의 hyper parameter 값을 찾는 것이다.
1. Double loop
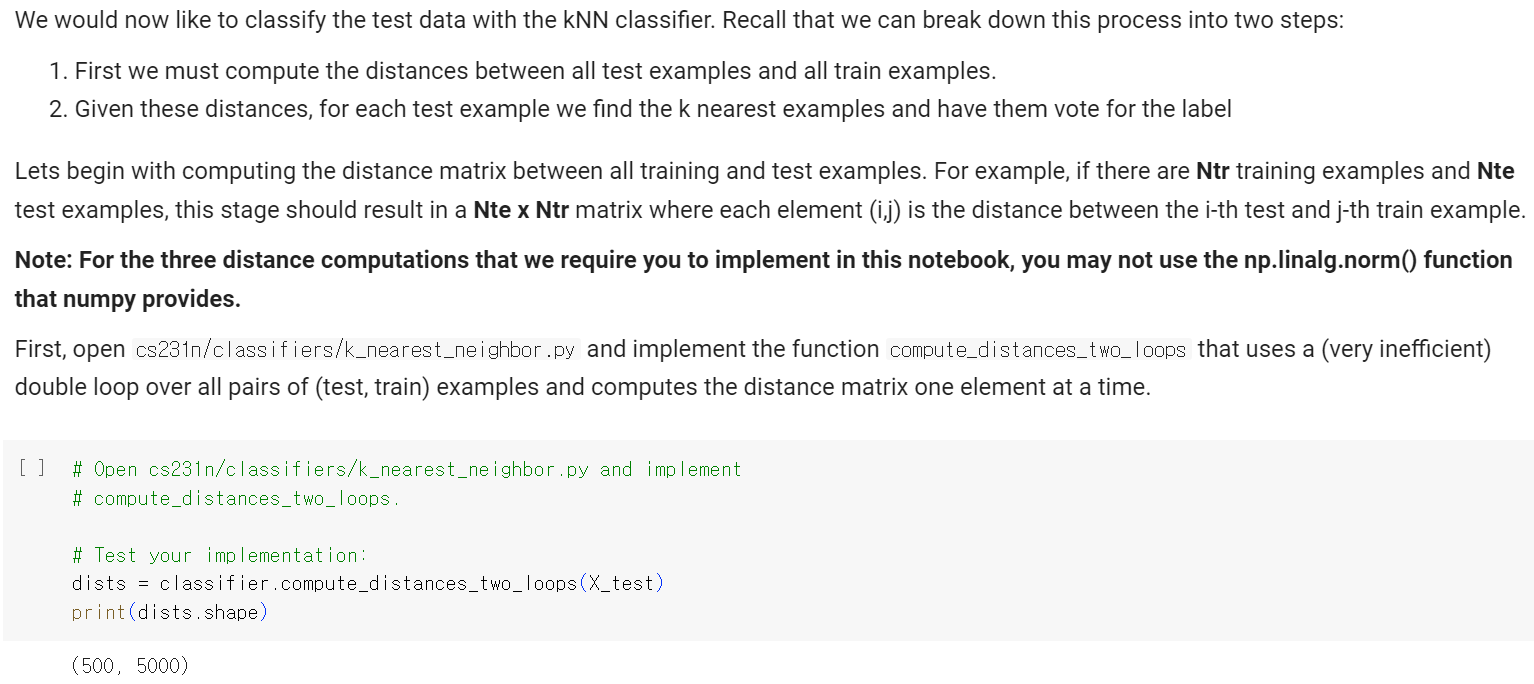
첫번째 구현은 l2 norm을 이용하여 각 pixel의 distance를 구하는 문제이다.
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
distance = np.array(self.X_train[j]-X[i]) ** 2
dists[i][j] = np.sqrt(np.sum(distance))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distscompute_distances_two_loops의 구조를 살펴보면 인수로 test_data X를 받고 리턴 값은 dists matrix이다.
dists maxtrix의 각 원소는 test_data와 train_data의 l2 norm을 저장한다.
dists matrix의 각 원소는 다음과 같이 표현된다.
dists matrix의 각 row는 test_data를 의미하고 각 column은 train_data를 의미한다.
예를 들어 dists[3][54]는 3번째 test_data와 54번째 train_data의 l2 distance를 의미한다.
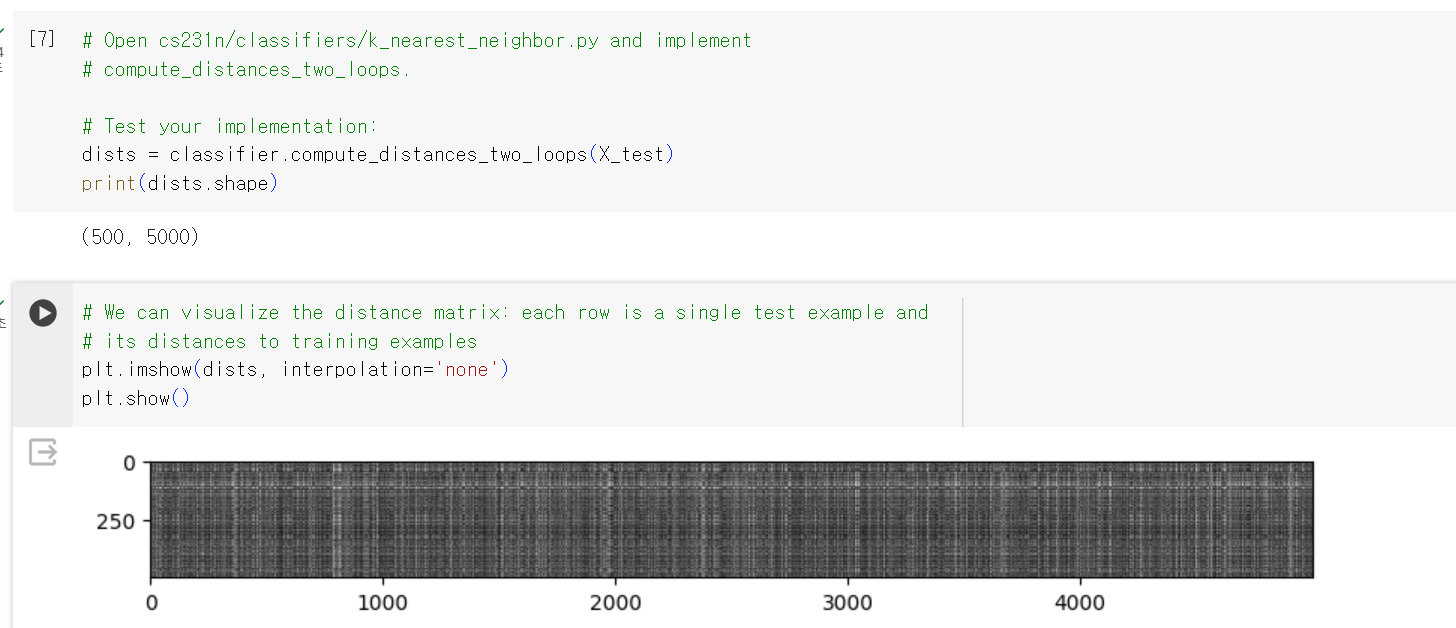
실제로 dists matrix를 시각화 하면 위와 같이 흑백 그림을 그릴 수 있다.
밝은 부분(흰색)은 l2 distance가 크다는 것을 의미하고 어두운 부분(검은색)은 l2 distance가 작다는 것을 의마한다.
2. One loop

두번째 구현은 for loop를 한번만 사용하는 것이다.
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i, :] = np.sqrt(
np.sum((self.X_train-X[i].reshape(1, X.shape[1]))**2, 1)
)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists코드의 구조는 직전의 코드와 거의 유사하다.
단지 for loop를 수행하는 부분이 약간 변했다.
이번에는 각 numpy에서 제공하는 broadcasting 기능을 이용하였다.
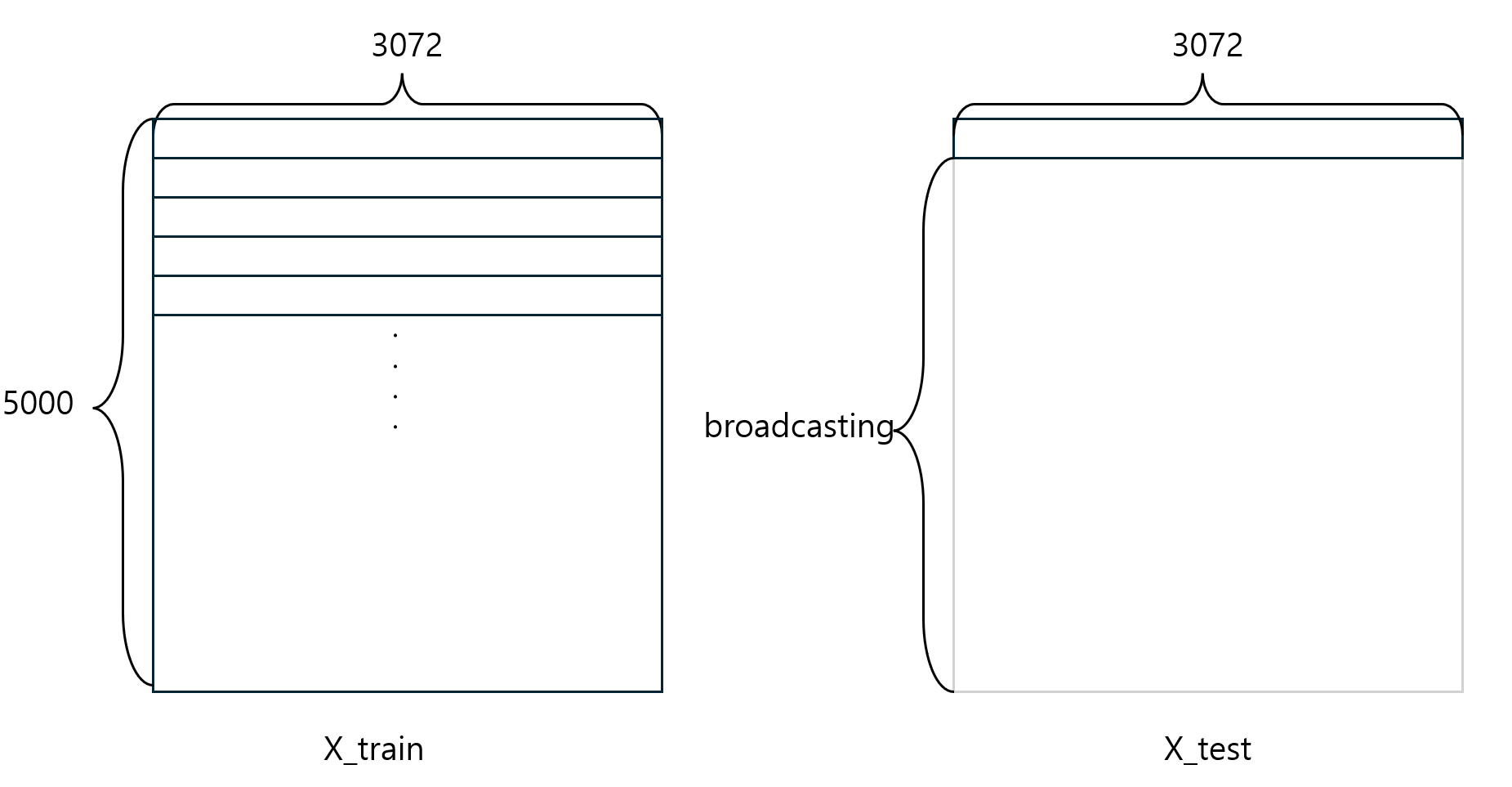
3. No loop

이번에는 loop를 하나도 사용하지 않고 구현하는 것이다.
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X2 = np.sum(X**2, axis=1).reshape(X.shape[0], 1)
Y2 = np.sum(self.X_train**2, axis=1).reshape(self.X_train.shape[0], 1)
Y2 = Y2.T
dists = np.sqrt(X2 + Y2 - 2 * np.dot(X, self.X_train.T))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsfor loop를 사용하지 않고 문제를 해결하기 위해서는 행렬 연산이 필요하다.
l2 distance의 식을 전개해보면 다음과 같이 표현된다.
행렬곱과 numpy의 broadcasting기능을 적절히 사용하면 위의 코드와 같이 표현가능하다.
4. Cross-validation
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds, axis=0)
y_train_folds = np.array_split(y_train, num_folds, axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
k_to_accuracies[k] = []
for i in range(num_folds):
x_train_fold = np.concatenate([x for num, x in enumerate(X_train_folds) if num != i],
axis = 0)
y_train_fold = np.concatenate([y for num, y in enumerate(y_train_folds) if num != i],
axis = 0)
classifier.train(x_train_fold, y_train_fold)
y_test_pred = classifier.predict(X_train_folds[i], k, 0)
num_correct = np.sum(y_test_pred == y_train_folds[i])
accuracy = float(num_correct) / X_train_folds[i].shape[0]
k_to_accuracies[k].append(accuracy)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy)) 마지막 문제는 적절한 hyper parameter를 찾기 위해서 Cross-validation을 시행하는 문제이다.
train_data를 총 5개의 fold로 구분하고 4개의 fold를 train_data로 나머지 1개의 fold를 test_data로 교차 검증을 시행한다.

k의 값에 따른 accuracy 분포
k가 크다고 해서 항상 좋은 결과가 나오는 것은 아니다.
