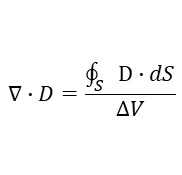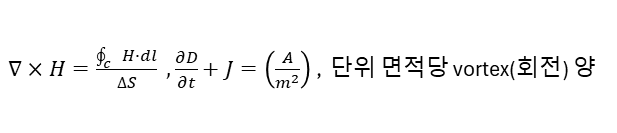목차
1. Intro
2. Maxwell equation Review
3. Coulomb's law
4. Ampere's law
5. Faraday's law
6. Magnetic Gauss's law
1. Intro
오늘은 학부 때 보통 1~2학년 때 배우는 전자기학의 리뷰를 하려고 한다. 본인의 대학교에서는 전자기학을 한 학기만 다뤘는데 Cheng의 전자기학 책을 사용하여 수업을 들었었다. 다른 학교는 전자기파까지는 나간다고 했던 것 같은데 본인의 학부는 맥스웰 방정식까지 진도를 나갔기 때문에 사실상 이 수업 때 전자기학2를 듣는 느낌이었다. 휘몰아치는 교수님의 수학 공식과 첫 날부터 1시간 15분을 풀로 채우시는 교수님의 엄청난 강의력 때문에 12명이 듣던 수업에서 다음 수업 때 7명으로 줄어 타노스되었다(그때 같이 탈출했어야 했다). 어쨌든 RF회로설계에서도 전자기파를 이해하려면 맥스웰 방정식이 중요하기 때문에 오늘 한번 주요 개념에 대해서 알아보도록 하자. 본인의 복습을 위해 작성한 것이기 때문에 반박은 언제든 환영하겠다.
2.Maxwell equation Review
맥스웰 방정식의 주요 개념은 여기서 찾아보도록 하자.
맥스웰 방정식은 전기와 자기의 발생, 전기장과 자기장, 전하 밀도와 전류 밀도의 형성을 나타내는 4개의 편미분 방정식이다. 다음 4개의 실험을 통해서 얻어졌다.
1. Coulomb's test :
전하(Q, charge), 전기장(E, electric field), 전속밀도(D, electric flux density), 유전율(permittivity) 등이 얻어진다.
2. Ampere's law
전류(I,current), 자기장(H,magnetic field), 자속밀도(B,magnetic flux density), 투자율(Permeability) 등이 얻어진다.
3. Faraday's law
magnetic flux가 시간에 따라 전압(V,voltage)를 만들어낸다.
4.Magnetic Gauss's law
어떤 면적을 잡더라도 자석의 N극과 S극이 폐루프를 잡고있다. 즉 들어가는 magnetic flux와 나가는 magnetic flux가 0이다. 자석이 잘라도 다시 N극 S극을 유지하는 것과 같음
3. Coulomb's law
쿨롱의 법칙으로 유명한 쿨롱이라는 사람이 뭔가 실험을 했다고 한다. 비틀림 저울을 이용해서 실험을 했다는데 두 전하 사이에 작용하는 힘을 구하고 싶었다고 한다. 이때 두 전하 사이에 작용하는 힘은 두 크기의 곱에 비례하고 거리의 제곱에 반비례한다는 것을 발견했다.
쿨롱 법칙:
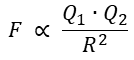
이때 실험을 통해서 비례상수를 찾게 되었고, 쿨롱 법칙은 다음과 같이 전개된다는 것을 찾았다.
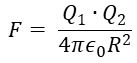
단위는 힘이기 때문에 N(뉴턴)이다.
여기서 epsilon0(ϵ0)는 유전상수라고 하는데 공기중(진공 상태)에서의 유전율(permittivity)을 나타낸다.
보통 이렇게 외워두면 나중에 계산할 때 편하다.
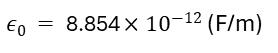
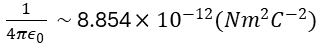
여기서 4𝜋는 어떤 구의 면적(R제곱)으로 정의하여 가정한다.
전기장의 정의: 단위 전하에 작용하는 힘
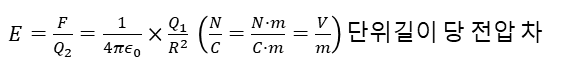
다음 식을 사용하여 어떤 면적에서의 전하 상의 거리에 따른 전압을 구할 수 있다.
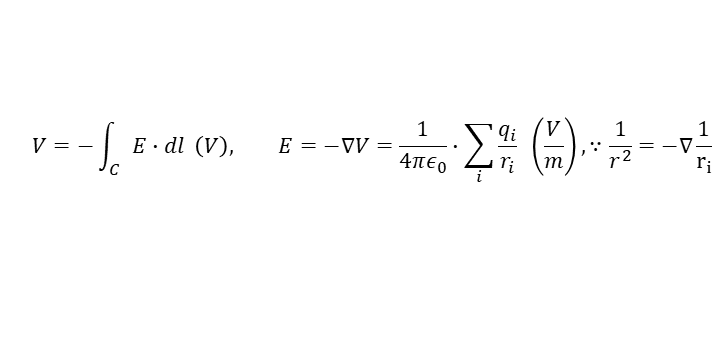
전속 밀도 (Electric Flux Density) : 단위면적당 전하량
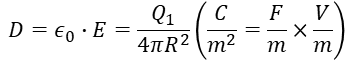
가우스 법칙 : 총 전하량은 전속 밀도를 적분한 값이다.
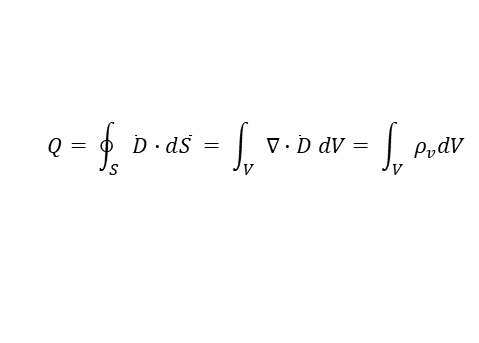
이는 divergence theorem을 이용하여 정리할 수 있다.
divergence theorem(발산정리) : 닫힌 표면
𝑆를 둘러싼 닫힌 부피 V에 대해, 벡터장의 부피 내 발산의 적분은 표면을 통해 흐르는 벡터장의 플럭스와 같다는 정리
즉 해당 이론에 따르면 표면적 적분을 부피적분으로 변환하는데 이것을 통해 KCL과 연관이된다. 들어가는 전류와 나가는 전류가 0을 잡고 있다.
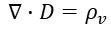
여기까지가 맥스웰 방정식의 첫번째 식이다.
4. Ampere's law
비례 상수 투자율(Permeability) :
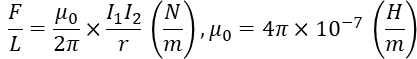
자속밀도 (Magenetic FLux Density)
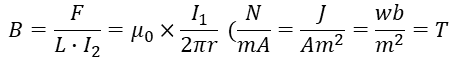
위의 자속 밀도 식을 사용하여 자기장(H)를 구할 수 있다.
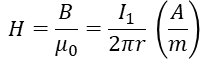
Ampere's law : 앰피어라는 분이 발견한 법칙. 전류는 자기장의 폐곡면에서의 선적분이다.는 자기장의 회전(전류밀도)을 면적에 대해서 적분한 것이다.
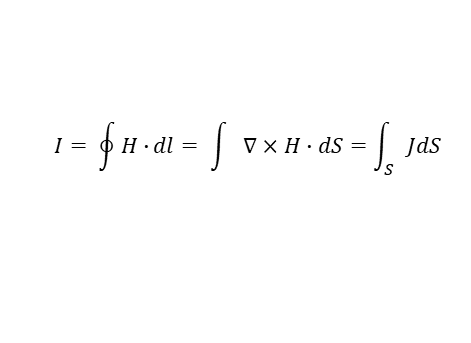
위와 같이 Stoke's Theorem으로 증명한다.
Stoke's Theorem :
벡터장의 회전(curl)에 대한 곡면적분은 경계선을 따라 벡터장의 선적분과 같다
5. Faraday's law of induction
자속의 변화에 비례해 억압하는 방향으로 전압이 발생한다.
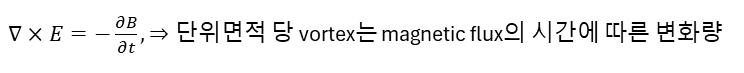
6. Magnetic Gauss's law
- 자기장의 Solenoidal 특성
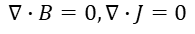
들어가는 전류와 나가는 전류가 balance를 이루므로 0이다. (KCL)
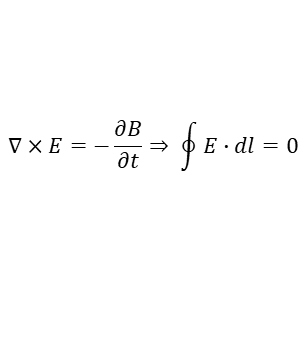폐곡선에서의 전기장의 합이 0이다. (KVL)
| 전기장 (Electric Field) | 전속 밀도 (Electric Flux Density) | 자기장 (Magnetic Field) | 자속 밀도 (Magnetic Flux Density) |
|---|---|---|---|
| ( E ) (V/m) | ( D ) (C/㎡) | ( H ) (A/m) | ( B ) (Wb/㎡) |
| ( \nabla \times E = -\frac{\partial B}{\partial t} ) | ( \nabla \cdot D = \rho_v ) | ( \nabla \times H = \frac{\partial D}{\partial t} + J ) | ( \nabla \cdot B = 0 ) |
| ( \oint_C E \cdot dl = -\frac{d\Psi}{dt} ) | ( \int_S D \cdot dS = Q ) | ( \oint_C H \cdot dl = I ) | ( \int_S B \cdot dS = 0 ) |
Electric field Vs Magnetic field
방향
전기장 : radial direction from a point charge, +에서 -로 방사형으로 흐른다.
자기장 : 오른손 법칙에 따라 전류 와이어 주위에 ㅡ른다.
Source:
전기장 : Charge 두개가 떨어지면 전기장이 생긴다.
자기장 : Charge의 움직임에 의해 생기게 된다.
Field Lines
전기장: +에서 -로 흐른다.
자기장: Circulal pattern이므로 시작과 끝이 없다.(net out flux)
Capacitor
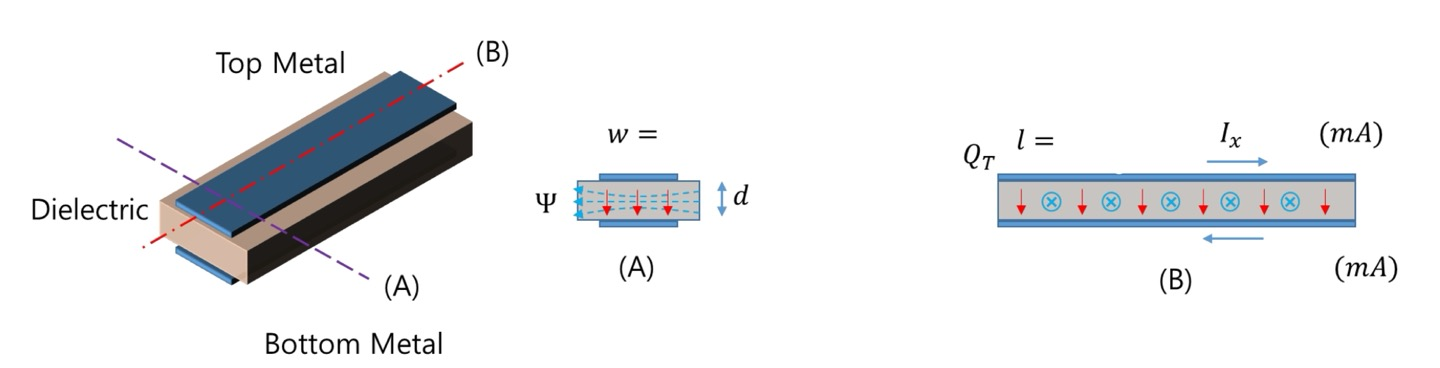
여기서 A는 Metal의 면적, d는 높이라고 할 때 표면에는 전기장이 없지만 Top과 Bottom의 사이(안쪽)에는 전기장이 존재한다.
Inductor
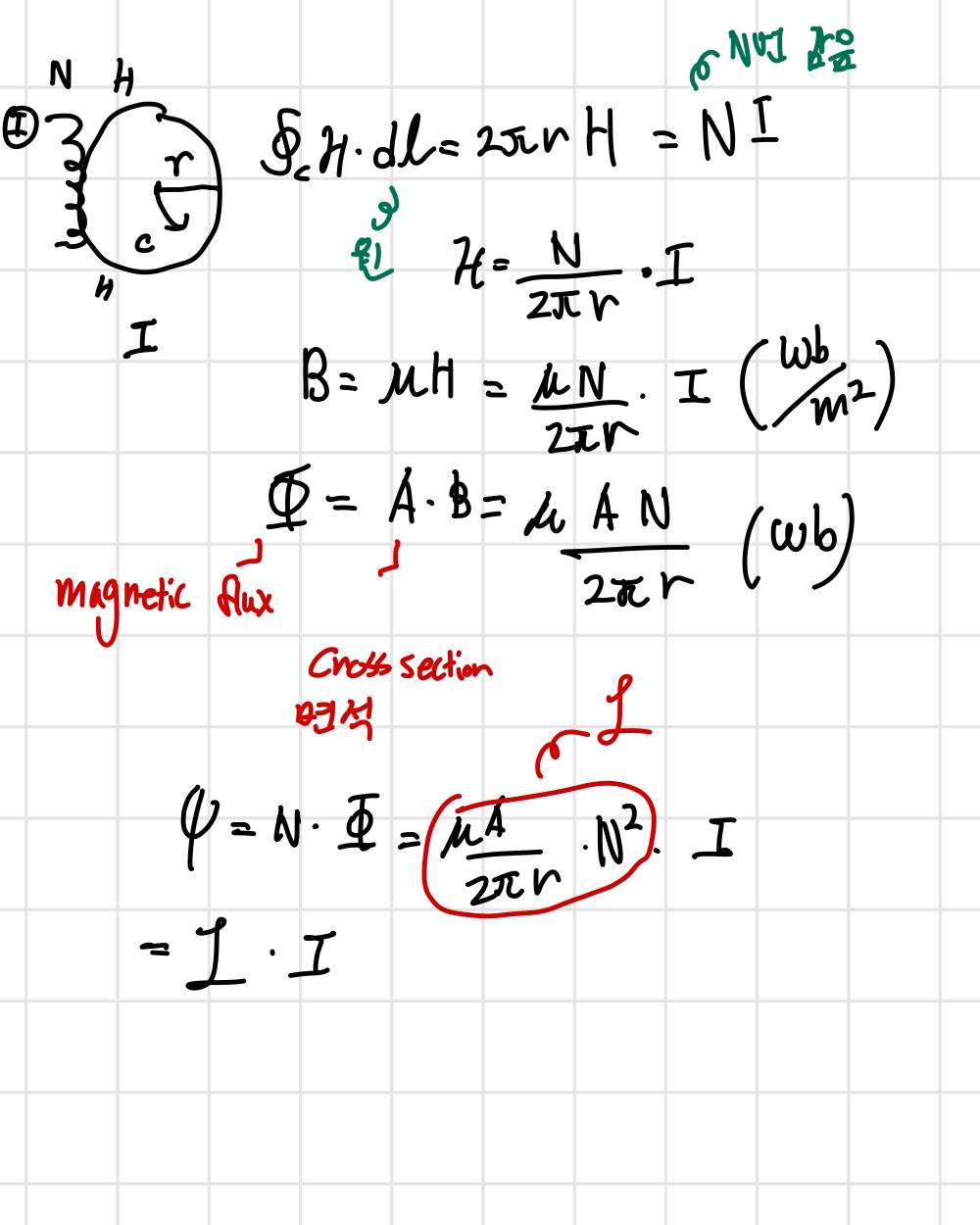
이상이다. 다음 장에서는 아마 관련 예제 풀이를 할 것 같다.
