데이터 구조란?
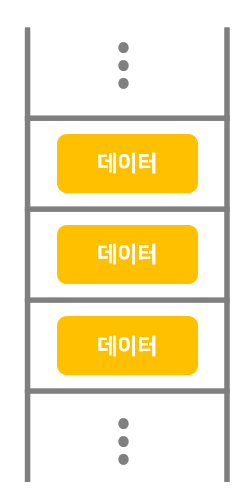
컴퓨터 안에서 데이터는 메모리에 저장이 된다.
메모리는 상자가 일렬로 나열된 형태를 하고 있다.
(하나의 상자 안에 하나의 데이터를 저장)
데이터 구조?
데이터를 메모리에 저장할 때 데이터의 순서나 위치 관계 등을 정하는 것
예시) 전화번호부의 데이터 구조
1) 위에서부터 차례대로 추가
종이에 적어서 관리하는 전화번호부를 관리하는 방법을 생각해보면,
가장 일반적인 방법은 전화번호를 추가할 때마다 종이 위에서부터 차례로 기입하는 방법이다.
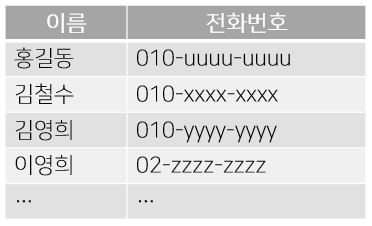
만약 '이철수'라는 사람을 찾아서 전화하고 싶다면,
전화번호는 단순히 번호를 받은 순서대로 기입돼 있으므로 어디에 적혀 있는지 알 수 없다.
따라서 앞에서부터 순서대로 찾는 방법밖에 없다.(혹은 '뒤에서부터'나 '임의로')
몇 건밖에 등록돼 있지 않다면 바로 발견할 수 있지만, 500건 정도가 되면 찾기 매우 힘들다.
2) 이름을 가나다순으로 관리
이름을 가나다순으로 관리한다면, 사전순으로 나열돼 있으므로 이 데이터들은 '데이터 구조' 가지고 있다.
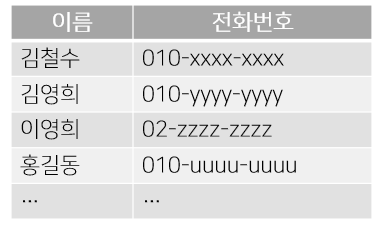
이 구조에서는 원하는 사람을 찾기가 쉽다. 이름의 첫 글자를 가지고 대략적인 위치를 추측할 수 있게 된다.
그렇다면 새로 알게 된 '이길동'이라는 사람의 번호를 추가한다면 어떻게 될까?
가나다순으로 등록한다는 규칙이므로 김영희와 이영희 사이에 추가해야 한다.
하지만 표에는 빈칸이 없으므로 이영희 이하의 전화번호를 하나씩 아래로 내려야 한다.
이를 위해서는 '행의 내용을 한 줄씩 아래로 내리고 원래 행을 지우는 작업'을 아래에서부터 순서대로 해야 한다.
하지만 500건의 데이터가 있다면 1건당 10초가 걸린다고 해도 1시간 이상의 시간이 걸리게 된다.
각각의 장단점
데이터가 온 순서대로 나열하는 방법은 데이터 추가 시 가장 뒤에 작성하면 되기 때문에 간단하지만,
검색이 필요할 때는 많은 시간이 걸린다.
반면에 데이터를 가나다순으로 나열하는 방법은 검색이 쉽지만 데이터 추가가 어렵다.
두 방법 모두 장단점이 있으며, 어느 방법을 선택할지는 전화번호부를 어떻게 사용할지에 달렸다.
한 번 만든 후 변경할 가능성이 없다고 하면 2번째 방법이 적합하고,
데이터 추가 빈도는 높지만 검색은 거의 하지 않는 경우라면 1번째 방법을 선택하는 것이 맞다.
선착순과 가나다순을 조합하면?
위 두 가지 방법을 섞어서 장단점을 보완하는 방법도 생각해 볼 수 있다.
'가행', '나행', '다행'과 같은 식으로 행마다 별도의 표를 만들어 관리하는 방법이다.
그러면 같은 표 내에서 데이터를 선착순으로 추가하면 된다.
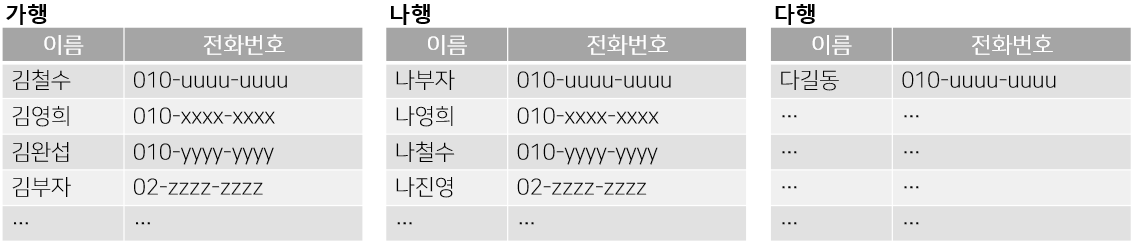
새로운 데이터를 추가할 때는 대응되는 표의 마지막에 추가하면 되고,
데이터를 검색할 때는 대응되는 표를 찾으면 된다.
이렇게 관리하더라도 각 표 안에서 처음부터 검색해야 하지만,
전화번호부 전체를 검색하는 것보다는 훨씬 낫다.
데이터 구조를 고민해서 메모리 이용 효율을 높인다.
데이터 구조에 대한 접근법도 이와 같다.
데이터를 메모리에 저장할 때 목적에 맞게 구조화해서 메모리의 이용 효율을 높여야 한다.
데이터는 메모리에 일직선으로 배치되지만, 포인터 등의 도구를 사용해서 '트리 구조'같은 복잡한 형태도 만들 수 있다.
리스트(list)
리스트는 데이터 구조의 하나로, 데이터를 일직선으로 나열한 형태를 가지고 있다.
데이터 추가나 삭제는 쉽지만, 원하는 데이터에 접근하려면 시간이 많이 걸린다.
- 리스트의 개념도
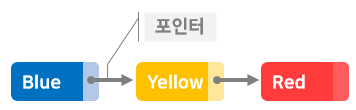
세 개의 문자열 'Blue','Yellow','Red'가 데이터로 저장되어 있다.
각 데이터에는 '포인터(pointer)'가 있으며, 다음 데이터의 메모리 위치를 가리킨다.
'Red'는 마지막 데이터이므로 'Red'포인터는 아무것도 가리키지 않는다.
리스트에서 데이터가 메모리상의 연속된 위치에 저장되지 않아도 되며,
일반적으로 떨어진 영역에 흩어져서 저장된다.
순차접근
흩어져 저장돼 있으므로 포인터를 처음부터 순서대로 따라가야만 원하는 데이터에 접근할 수 있다.
- 이것을 '순차 접근' 또는 '시퀀셜 액세스(sequential access)'라고 한다.
예를 들어, 'Red'에 접근하고 싶은경우는 먼저 'Blue'에 접근한 뒤 'Yellow'를 가야만 'Red'에 접근할 수 있다.
데이터 추가
추가할 위치의 앞 뒤 포인터를 변경만 하면 되므로 간단하다고 볼 수 있다.
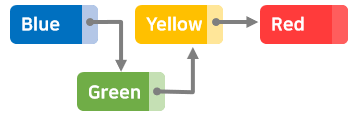
예를 들어, 'Blue'와 'Yellow' 사이에 'Green'을 추가하고 싶을 때
'Blue'의 포인터를 'Green'을 가리키도록 변경하고, 'Green'포인터를 'Yellow'를 가리키도록 하면 된다.
데이터 삭제
데이터 추가와 같은 방식으로 포인터의 방향을 바꾸면 된다.
예를 들어, 'Yellow'를 삭제하는 경우
'Green' 포인터를 'Yellow'가 아닌 'Red'로 변경하면 삭제가 완료된다.
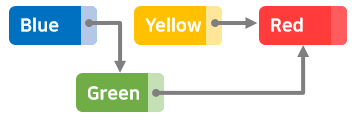
'Yellow'는 메모리에는 남지만 어디에서도 접근할 수 없으므로 일부러 삭제할 필요는 없고
이후에 이 영역이 사용될 때 덮어쓰기가 되어 다시 사용할 수 있게 된다.
계산 시간
리스트에 저장되어 있는 데이터 수가 n이라면, 데이터에 접근할 때에는 리스트의 앞에서부터 차례로 진행하기 때문에(선형 탐색) 접근하고 싶은 데이터가 뒤쪽에 있는 경우에는 O(n)의 계산 시간이 걸린다.
반면, 데이터 추가와 삭제는 해당 위치에 이미 접근해 있는 것을 전제로 두 개의 포인터만 변경하면 되기에 n에 상관없는 상수 시간 O(1)이 된다.
원형 리스트와 양방향 리스트
- 원형 리스트
마지막 데이터 포인터가 선두를 가리키도록 하면 원형으로 연결이 된다.
이것을 '원형 리스트' 또는 '순환 리스트'라고 한다.
원형 리스트에는 선두나 후미라는 개념이 없다.
- 양방향 리스트
각 데이터가 포인터 두 개를 사용해서 앞뒤 데이터를 가리키도록 한 '양방향 리스트'가 있다.
리스트를 앞에서 뒤로, 뒤에서 앞으로도 추적할 수 있게 하여 편리하다.
단, 양방향 리스트에서는 포인터 수가 늘어나므로 데이터 저장을 위한 영역이 많아지는 결점이 있다.
또한 데이터 추가나 삭제 시에도 변경해야 할 포인터가 늘어난다.
배열
배열은 데이터 구조의 하나로, 데이터를 1열로 나열한 것이다.
리스트와 대조적으로 데이터에 접근하기는 쉽지만 추가나 삭제에 시간이 걸린다.
- 배열의 개념도

세 개의 문자열 'Blue','Yellow','Red'가 데이터로 저장되어 있다.
a라는 것은 배열의 이름이고, 그 뒤에 []안에 있는 숫자는 배열의 몇 번째 요소인지를 가리킨다.
예를 들어, a[2]의 'Red'는 배열 a의 세 번째 요소가 된다.
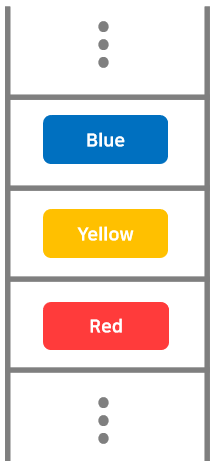
데이터는 연속된 메모리 영역에 순서대로 저장된다.
연속된 영역에 저장돼 있어서 첨자를 사용해서 메모리의 주소를 계산할 수 있다.
따라서 각 데이터에 바로 접근할 수 있는데, 이것을 '임의 접근(random access, 랜덤 액세스)'이라고 한다.
임의 접근
예를 들어, 'Red'에 접근하고 싶다면, a[2]라고 지정하기만 하면 직접 'Red'에 접근할 수 있다.
배열은 임의의 위치에 데이터를 추가, 삭제해야 하는 경우에 리스트에 비해 많은 시간이 걸리는 단점이 있다.
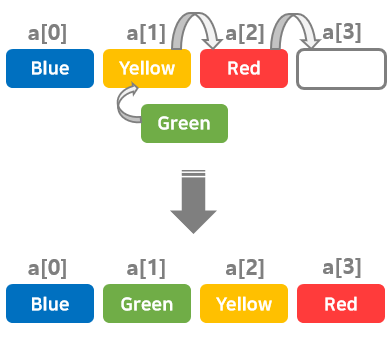
예를 들어, 'Green'을 두번째 요소(a[1])에 추가하는 경우.
먼저 배열의 마지막에 추가를 위한 공간을 확보하고 하나씩 데이터를 옆으로 이동하여
빈 공간에 'Green'을 추가한다.
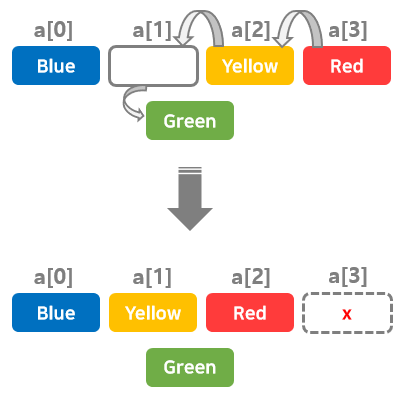
반대로, 'Green'을 삭제할 때는 요소를 삭제하고,
빈 곳을 하나씩 왼쪽으로 옮겨서 자리를 메꾼 뒤 남은 공간을 삭제한다.
계산 시간
배열에 저장된 데이터의 수를 n이라고 할 때, 임의 접근할 수 있으므로 상수 O(1)의 계산 시간으로 데이터에 접근할 수 있다.
반면, 데이터를 추가할 때는 추가할 곳보다 뒤에 있는 모든 데이터를 하나씩 옮겨야하므로 배열의 선두에 데이터를 추가하려고 하면 O(n) 시간이 걸린다. (= 삭제)
리스트와 배열 모두 데이터를 1열로 나열하는 데이터 구조이지만, 무엇을 사용할지는 어떤 작업을 자주하는지 고려해서 정하면 된다.
접근 추가 삭제 리스트 느림 빠름 빠름 배열 빠름 느림 느림
스택(stack)
스택은 데이터 구조의 하나로서 데이터를 1열로 나열하지만, 서류를 쌓아 놓은 경우처럼 새롭게 추가한 데이터에만 접근할 수 있다. 새로운 서류가 도착하면 현재 서류 더미의 가장 위에 올려두고 서류를 꺼낼 때는 가장 위에서부터 꺼내는 것과 같다.
푸시(push) : 데이터 추가
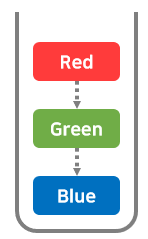
스택에 데이터를 추가하는 작업을 '푸시(push)'라고 한다.
스택에 데이터를 추가할 때는 가장 위에 추가가 된다.
팝(pop) : 데이터 추출
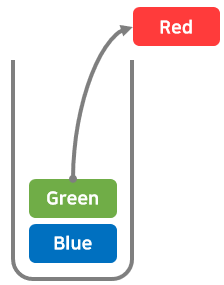
스택에서 데이터를 꺼내는 작업을 '팝(pop)'이라고 한다.
스택에서 데이터를 꺼내는 경우도 가장 위, 가장 최근에 추가된 데이터부터 꺼낸다.
후입선출 구조 : LIFO(Last In First Out)
스택처럼 나중에 넣은 것을 먼저 꺼내는 후입선출 구조를 'Last In First Out'이라고 하며,
앞글자만 따서 'LIFO'라고도 한다.
리스트나 배열과 마찬가지로 스택도 데이터를 1열로 나열한 것이지만
데이터 추가나 삭제가 단방향으로만 가능하다는 제약이 있다.
또한 데이터 접근도 스택의 가장 위에 있는 데이터만 가능해서 중간에 있는 데이터가 필요하다면
해당 데이터가 제일 위로 올라올 때까지 pop해야 한다.
활용 예
항상 최신 데이터만 접근할 수 있도록 하는 구조에서 편리하게 사용된다.
예를 들어, (AB (C (DE) F) (G ((H) IJ) K))라는 문자열의 괄호 대응 관계를 결정하고 싶다했을 때,
왼쪽부터 문자열을 읽어서 왼쪽 괄호가 나올 때마다 그 위치를 스택에 푸시한다.
오른쪽 괄호가 나오면 팝을 해서 데이터를 꺼내면 해당 괄호에 대응하는 왼쪽 괄호의 위치라는 것을 알 수 있다.
'깊이 우선 탐색'에서는 탐색 후보 중에서 항상 최신의 것을 선택해야 하며, 이때 후보 관리에 스택을 사용할 수 있다.
큐(Queue)
큐는 데이터 구조의 하나로 데이터를 1열로 나열하는 구조이다.
스택과 비슷하지만 큐는 추가하는 측과 삭제하는 측이 반대이다.
큐는 '대기 행렬'이라고 불리는데 줄 서 있는 행렬이라는 의미이다.
행렬에서는 새롭게 온 사람이 가장 뒤에 서며, 가장 앞에 있는 사람부터 순서대로 처리된다.
인큐(enqueue) : 데이터 추가
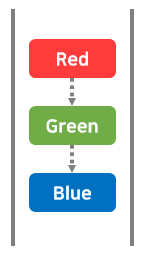
큐에 데이터를 추가하는 작업을 '인큐(enqueue)'라고 한다.
큐에 데이터를 추가하면 가장 위에 추가된다.
디큐(dequeue) : 데이터 추출
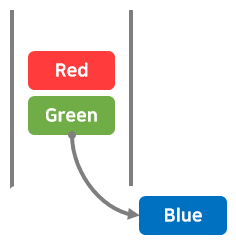
큐에서 데이터를 꺼내는 작업을 '디큐(dequeue)'라고 한다.
큐에서 데이터를 꺼낼 때는 가장 아래, 가장 오래된 데이터부터 꺼낸다.
선입선출 구조 : FIFO(First In First Out)
큐와 같이 먼저 넣은 것을 먼저 꺼내는 선입선출 구조를 'First In First Out'라고 하며,
앞글자만 따서 'FIFO'라고 한다.
스택과 마찬가지로 데이터를 조작할 수 있는 위치가 정해져 있는데,
큐에서는 추가하는 쪽과 삭제하는 쪽이 반대여서 스택과 마찬가지로 중간에 있는 데이터에 접근할 수 없으므로
필요한 데이터가 나올 때까지 디큐를 해야 한다.
활용 예
오래된 데이터부터 순서대로 처리해야 하는 것은 매우 자연스러운 방식이어서 큐는 폭넓게 활용되고 있다.
'너비 우선 탐색'에서는 탐색 후보 중에서 항상 가장 오래된 것을 선택하므로 후보 관리에 큐를 활용한다.
해시 테이블(hash table)
해시 테이블은 데이터 구조의 하나이다. '해시 함수'와 함께 데이터 검색을 효율적으로 하기 위해 사용되는 구조다.
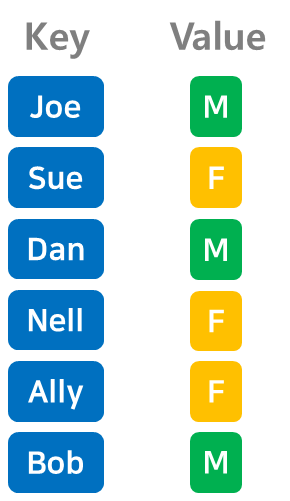
해시 테이블은 키(Key)와 값(Value)이 한 쌍을 이루는 데이터를 저장한다.
위 그림에서는 각 사람의 성별을 데이터로 저장하고 있으며, 이름을 키로, 성별을 값으로 저장하고 있다.
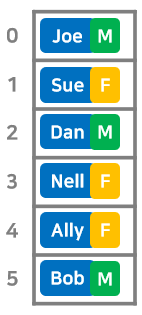
해시 테이블의 특징을 비교하기 위해 6개로 상자로 이루어진 배열에 데이터를 저장한다.
Ally의 성별을 알고 싶은데 배열의 몇 번째에 저장되어 있는지 모르므로 앞에서부터 차례대로 확인해야 한다.(선형 탐색)
선형 탐색은 데이터양에 비례해서 계산 시간이 늘어난다.
배열 탐색에 시간이 걸리므로 탐색에는 적합하지 않은 구조라는 것을 알 수 있다.
이 문제를 해결해주는 것이 해시 테이블이다.
'해시 함수'를 이용해서 키에 해당하는 해시값을 계산한다.
구한 해시값을 배열의 수로 나누어 나머지를 구한 뒤 (나눗셈의 나머지를 구하는 연산 'mod')
구한 수와 같은 배열의 상자에 저장한다.
| Key | hash값 | mod연산 | 배열숫자 |
|---|---|---|---|
| Joe | 4928 | mod 5 | 3 |
| Sue | 7291 | mod 5 | 1 |
| Dan | 1539 | mod 5 | 4 |
| Nell | 6276 | mod 5 | 1 |
| Ally | 9143 | mod 5 | 3 |
| Bob | 5278 | mod 5 | 3 |
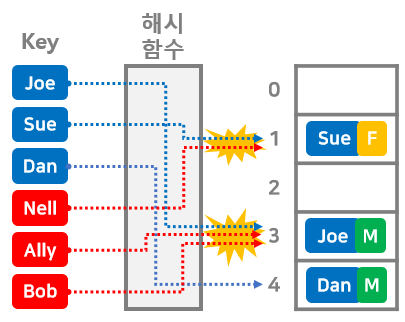
Nell의 데이터가 저장될 위치(1번)에는 이미 Sue의 데이터가 저장되어 있다.
그리고 Ally, Bob데이터가 저장될 위치(3번)에도 Joe가 저장되어 있다.
이렇게 데이터 저장 위치가 겹치는 것을 '충돌'이라고 한다.
이런 경우에는 리스트 구조로 기존 데이터와 연결한다.
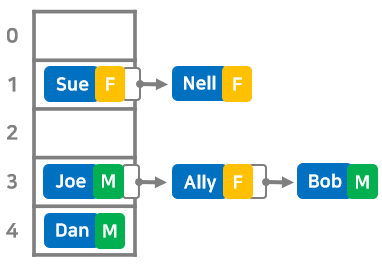
데이터 검색 방법
Dan의 성별을 확인하고 싶은 경우.
Dan이 배열의 몇 번 상자에 저장돼 있는지 알기 위해서 Key인 'Dan'의 해시값을 구하고
배열의 상자 수인 5로 mod 연산을 한다.
결과는 4이므로 4번 상자에 저장돼 있는 것을 알 수 있다.
4번 상자에가서 'Dan'과 일치하는 데이터의 대응 값을 추출하면 성별을 알 수 있다.
리스트로 연결되어 있는 데이터인 경우 해당 데이터를 선두로 만들어진 리스트를 선형 탐색을 실시한다.
특징
해시 테이블은 해시 함수를 이용해서 배열 내의 특정 데이터에 빠르게 접근할 수 있다.
해시값이 충돌할 때는 리스트를 이용하고 있어서 저장할 데이터 수가 정해져 있지 않더라도 유연하게 대응할 수 있다.
해시 테이블에 사용하는 배열의 크기는 너무 작으면 충돌이 많아지고 선형 탐색의 빈도가 높아지게 된다.
반대로 크기가 너무 크면 데이터가 없는 사자가 많아져서 메모리를 낭비하게 된다.
따라서, 배열의 크기를 적절히 설정하는 것이 좋다.
리스트를 사용하여 기존 데이터 뒤에 연결하는 방법을 '연쇄법(또는 체이닝(chaining)'이라고 한다.
충돌 시의 처리 방법에는 연쇄법 이외에도 몇 가지가 있다.
- 개방 주소법(open addressing)
- 충돌이 발생한 경우 다음 후보가 될 주소(배열상의 위치)를 구해서 거기에 저장하는 방식이다.
- 해당 주소에도 데이터가 존재한다면 다음 후보 주소를 구하며 비어 있는 곳을 찾을 때까지 다음번 주소를 구한다.
- '다음 주소'를 어떻게 구하는가는 해시 함수를 여러 개 사용하는 방법이나 '선형 탐사'등 몇 가지 방법이 있다.
데이터의 유연한 저장과 빠른 접근이 가능한 해시 테이블은 프로그래밍 언어의 연관 배열(associative array)등에 사용되고 잇다.
힙(heap)
힙은 그래프의 트리 구조 중 하나로 '우선순위 큐(queue)'를 구현할 때 사용된다.
우선순위 큐는 데이터 구조의 하나로서 데이터를 자유롭게 추가할 수 있다.
반면, 데이터를 추출할 때는 최솟값부터 순서대로 선택된다.
추가는 자유롭게 하고 추출할 때는 작은 값부터 꺼내느 것이 우선순위큐이다.
또한 힙을 표현하는 트리 구조에서는 각 정점을 '노드(node)'라고 부른다.
힙에서는 각 노드에 데이터가 저장된다.
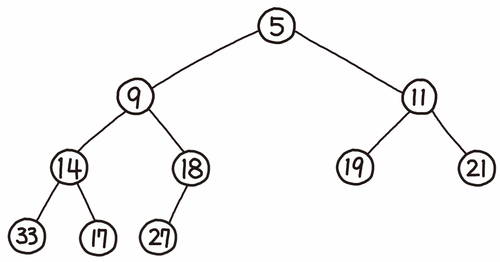
힙의 각 노드에 데이터가 저장되어 있고, 최대 두 개의 자식 노드를 가진다.
트리의 모양은 데이터의 개수에 의해 정해진다.
노드는 위에서부터 채워지며, 같은 층(단)에서는 왼쪽부터 채워진다.
힙에서는 데이터 저장 위치를 정하기 위해 자식 노드의 숫자는 반드시 부모의 숫자보다 커야 한다는 규칙이 있다.
따라서 가장 위(뿌리)에 가장 작은 숫자가 들어있다.
데이터를 추가할 때는 이 규칙을 지키기 위해 가장 아래층에 있는 왼쪽 노드부터 값을 채운다.
가장 아래 층이 모두 채워지면 새로운 층을 만들어서 가장 왼쪽에 채운다.
데이터 추가
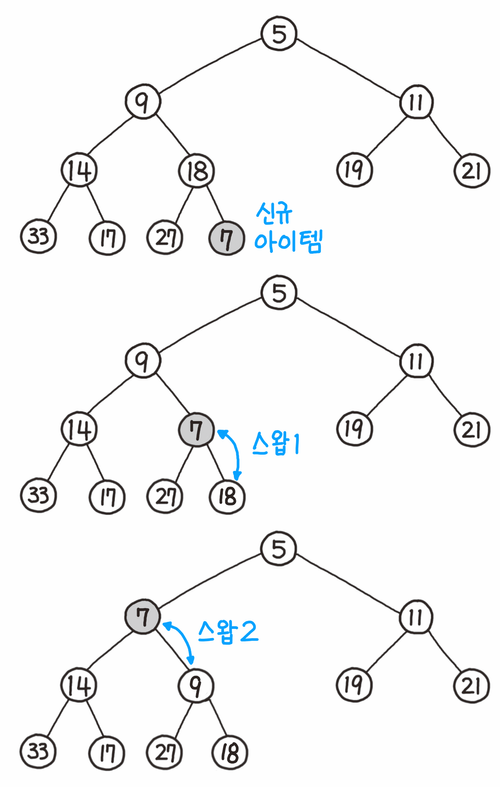
가장 아래층 남아있는 자리에 데이터가 추가된다.
부모의 숫자가 클 때는 조건을 만족하지 않으므로 부모와 자식을 교환한다.
규칙에 맞으면 그대로 두며, 이런 처리를 교환이 발생하지 않을 때까지 반복한다.
데이터 삭제
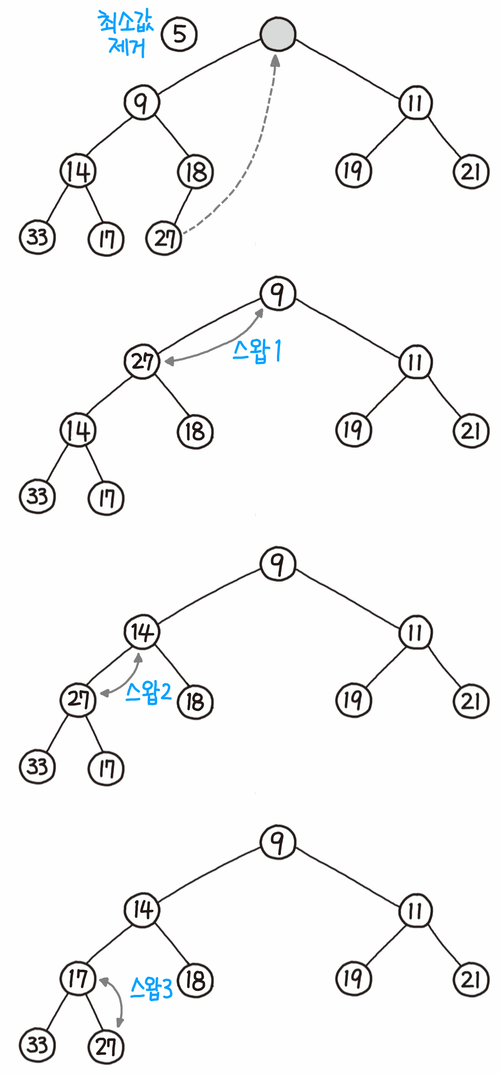
힙에서 숫자를 꺼낼 때는 가장 위에 있는 루트 노드가 추출된다.
힙에서 가장 위에 있는 숫자가 최솟값을 지니고 있기 때문이다.
힙의 구조를 다시 정리해야 하는데, 가장 후미에 있는 숫자를 가장 위로 이동한다.
부모 숫자보다 자식 숫자가 작은 경우는 자식의 좌우에 있는 숫자 중 더 작은 쪽과 교환한다.
이 처리를 교환이 발생하지 않을 때까지 반복한다.
계산시간
힙은 항상 가장 위에 최솟값이 있으므로 데이터 수에 상관없이 O(1) 시간에 최솟값을 추출할 수 있다.
추출한 후 힙을 재구축할 때에는 가장 후미에 있는 데이터를 가장 위로 가져온 후 자식과 비교해가며 아래 방향으로 진행한다.
이 때문에 계산시간은 트리의 높이와 비례하게 된다.
힙 형성 조건에 따라 트리의 높이는 logn 이므로 재구축의 계싼 시간은 O(log n)이 된다.
데이터추가도 마찬가지로 O(log n)이 된다.
활용 예
관리하고 있는 데이터 중에서 최솟값을 자주 추출해야 하는 경우에는 힙이 편리하다.
예를 들어, 다익스트라 알고리즘에서는 후보가 되는 노드 중에서 최솟값을 매 단계에서 선택하는데,
이때 노드를 관리하기 위해 힙을 사용하는 경우도 있다.
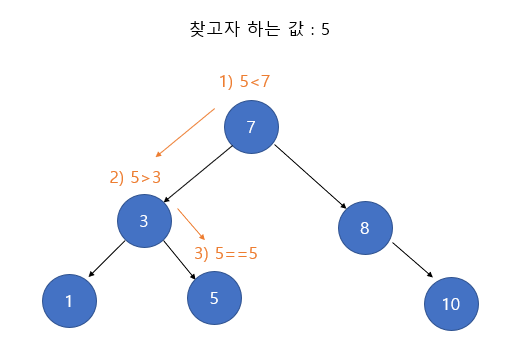
이진 탐색 트리(binary search tree)
이진 탐색 트리는 데이터 구조의 하나로, 그래프의 트리 구조를 사용한다.
이진탐색 트리에서는 각 노드에 데이터가 저장된다.
각 노드는 최대 두 개의 자식노드를 가진다.
이진 탐색 트리는 두 가지 성질을 지닌다.
1. 모든 노드는 왼쪽 가지에 포함되는 어떤 숫자보다도 큰 숫자가 된다.
2. 모든 모드는 그 노드의 오른쪽 가지에 포함되는 어떤 숫자보다 작은 숫자가 된다.
이 두 개의 성질로부터 다음 조건이 성립된다.
- 이진 탐색 트리의 최소 노드는 최상단에 있는 노드로부터 왼쪽 가지만 계속 따라가면 나오는 가장 끝에 있는 노드가 된다.
- 이진 탐색 트리에서 최대 노드는 최상단의 노드로부터 오른쪽 가지만 계속 따라가면 나오는 가장 끝에 있는 노드가 된다.
데이터 추가
이진 탐색 트리의 최상단 노드부터 탐색한다. 추가하려고 하는 데이터를 현재 노드 값과 비교해서
작으면 왼쪽으로 크면 오른쪽으로 진행한다. 노드가 없으면 새로운 노드를 추가한다.
데이터 삭제
자식 노드가 없는 노드는 대상 노드만 삭제하면 작업이 끝난다.
자식 노드가 하나인 노드를 삭제할 때는 대상 노드를 삭제하고 삭제한 노드의 위치로 자식 노드를 이동시키면 된다.
자식 노드가 두 개인 경우는 대상 노드를 삭제하고 삭제한 노드에서 왼쪽 가지의 최대 노드를 찾는다.
- 혹은 오른쪽 가지의 최소 노드를 찾아도 된다.
삭제한 노드의 위치로 이동시키면 이진 탐색 트리의 성질을 유지하면서 노드를 삭제할 수 있다.
이동 대상 노드도 자식 노드를 지니는 경우에는 같은 처리를 재귀적으로 반복하면 된다.
데이터 탐색
최상단 노드부터 탐색을 시작한다. 현재 노드값과 비교해서 작으면 왼쪽, 크면 오른쪽으로 탐색을 진행한다.
계산 시간
트리의 높이만큼만 비교하면 되므로 노드가 n개 있고 트리가 균형 잡힌 경우라면 최대 logn회의 비교로 이동할 수 있다.
따라서 계산 시간은 O(log n)이 된다.
단, 트리가 한쪽으로 치우쳐서 직선에 가까운 모양인 경우에는 트리가 높아져서 O(n)이 될 수 있다.
이진 탐색 트리를 확장한 데이터 구조는 여러 개가 있다. 예를 들어, 트리가 한쪽으로 치우친 경우 모양을 바로잡기 위해 항상 균형을 유지하도록 하는 구조도 있다.
'자가 균형 이진 탐색 트리(self-balancing binary search tree)'라고 하며, 탐색 효율을 유지할 수 있다.
이진 탐색 트리에서는 하나의 노드가 가질 수 있는 자식 노드가 최대 두개였지만, 이것을 m개로 확장해서 자식 수에 제한을 두지 않고 트리의 균형을 도모한 'B트리'라는 것도 있다.
Reference
- 『알고리즘 도감』, 이시다 모리테루, 미야자키 쇼이치 - 제이펍