[알고리즘] 이분 탐색(Binaray Search)

정렬되어 있는 배열에서 데이터를 찾으려고 시도할 때,
순차탐색처럼 처음부터 하나씩 모든 데이터를 체크하여 값을 찾는 것이 아니라
탐색 범위를 절반씩 줄여가며 찾아가는 방법이다.

• 주요 조건은 정렬되어 있는 배열
• 변수 3개를 사용하여 탐색한다.
  • start, end, mid
• 찾으려는 데이터와 중간점위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는다.

작동예시

출처 https://velog.io/@kimdukbae/%EC%9D%B4%EB%B6%84-%ED%83%90%EC%83%89-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-Binary-Search

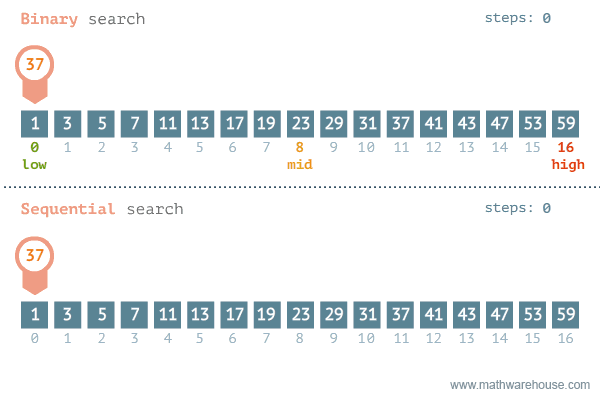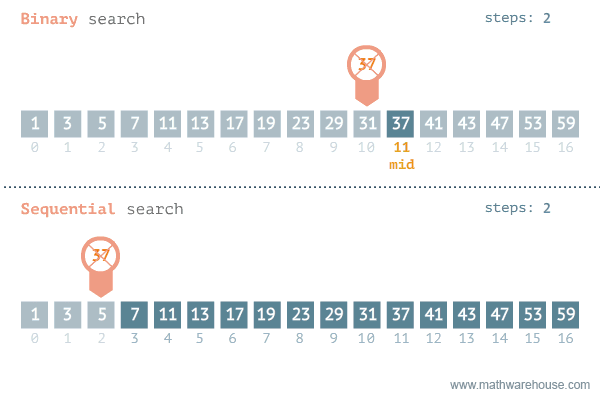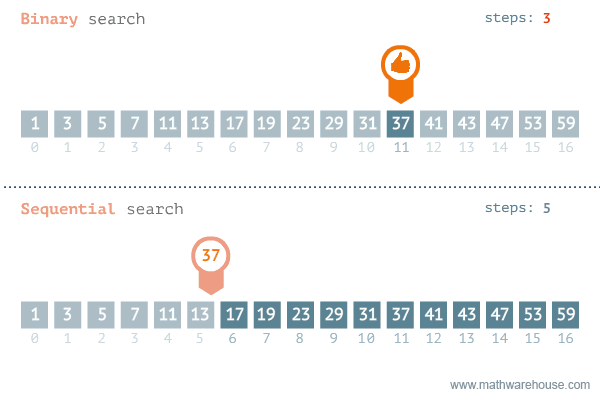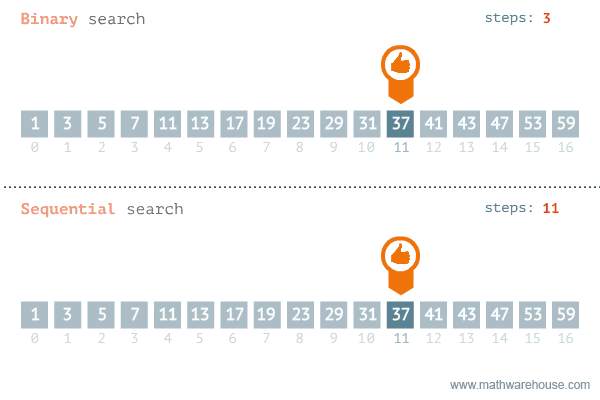
출처 https://namu.wiki/w/%EC%9D%B4%EC%A7%84%20%ED%83%90%EC%83%89

출처 https://namu.wiki/w/%EC%9D%B4%EC%A7%84%20%ED%83%90%EC%83%89

재귀적 이진 탐색(이분 탐색)

def binary_search(array, target, start, end):
    if start > end: return None

    mid = (start + end) // 2

    # 원하는 값 찾은 경우 인덱스 반환
    if array[mid] == target: return mid
    # 원하는 값이 중간점의 값보다 작은 경우 왼쪽 부분(절반의 왼쪽 부분) 확인
    elif array[mid] > target: return binary_search(array, target, start, mid - 1)
    # 원하는 값이 중간점의 값보다 큰 경우 오른쪽 부분(절반의 오른쪽 부분) 확인
    else: return binary_search(array, target, mid + 1, end)

비재귀적 이진 탐색(이분 탐색)

def binary_search(array, target, start, end):

    while start <= end:

        mid = (start + end) // 2

        if array[mid] == target: return mid
        # 원하는 값이 중간점의 값보다 작은 경우 왼쪽 부분(절반의 왼쪽 부분) 확인
        elif array[mid] > target: end = mid - 1
        # 원하는 값이 중간점의 값보다 큰 경우 오른쪽 부분(절반의 오른쪽 부분) 확인
        else: start = mid + 1
    return None

시간복잡도

처음부터 끝까지 원하는 값을 찾을 때까지 탐색을 계속하는 순차 탐색은 Worst Case일 때 $O(n)$이라는 시간복잡도를 보여준다. 10만개의 데이터가 있다면 무려 10만번을 탐색해야 하는 것이다.

그러나, Binary Search는 탐색 대상을 절반씩 계속해서 줄여나가기 때문에, Worst Case일 때에도 탐색의 횟수가 $O(log_{2}n)$ 이 되므로 10만개의 데이터가 있다고 하더라도 약 16번 정도로 탐색을 끝낼 수 있다.

즉, 이진 탐색(이분 탐색)은 탐색 범위를 절반씩 줄이고, $O(log_{2}n)$의 시간 복잡도를 보장한다.