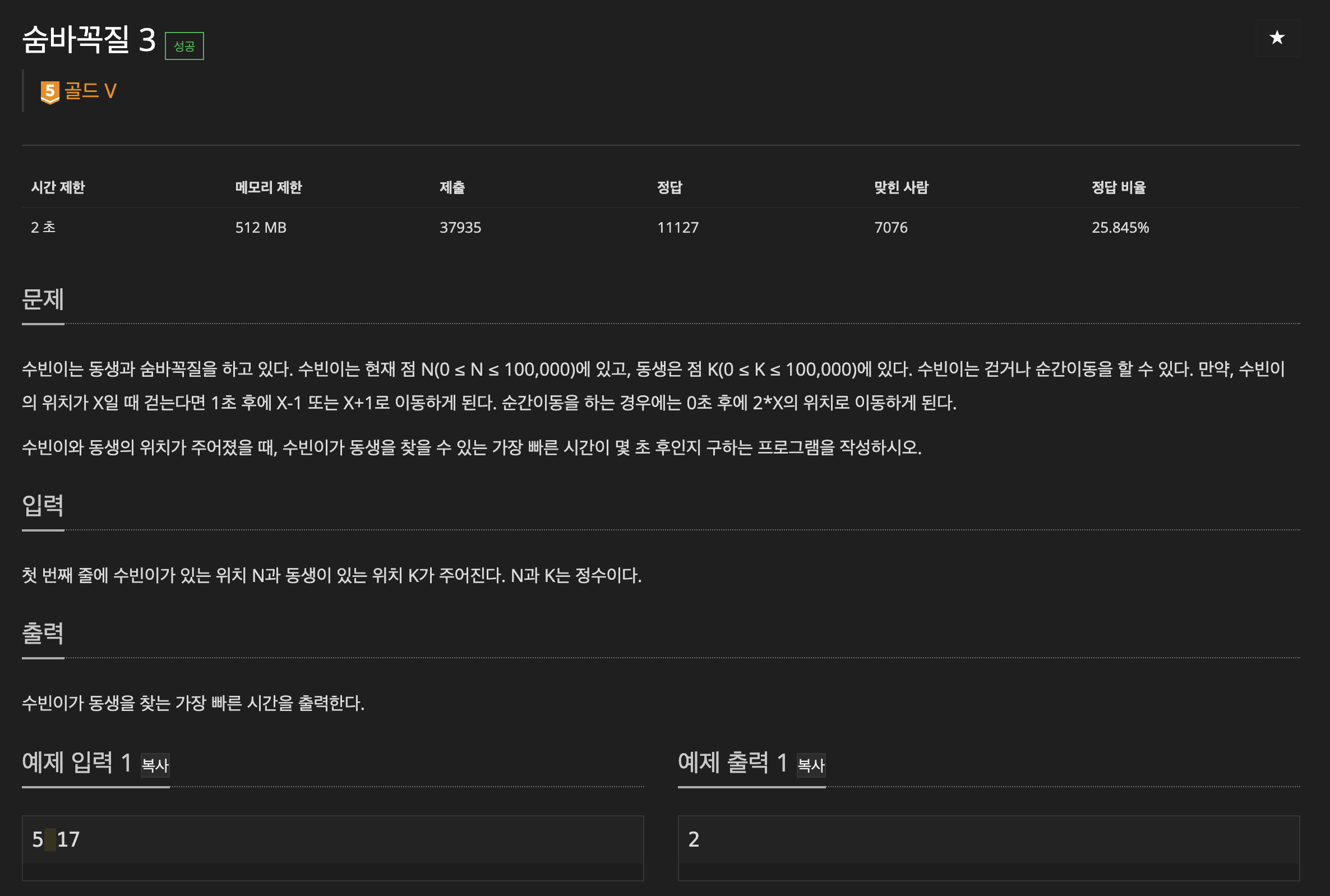
https://www.acmicpc.net/problem/13549
풀이 ① - 다익스트라
1. 아이디어
-
목표 지점을 찾으면 탐색을 종료하는, 일반적인 DFS, BFS는 간선의 가중치가 모두 같아야 함.
하지만, 본 문제는 +1, -1 로 가는 경우 가중치가 1,
x2 로 가는 경우 가중치가 0 으로 가중치가 다름 -
간선의 가중치가 같지 않고, 탐색 시작 지점이 1개이므로
BFS 가 아닌 다익스트라 이용
=> 시작 지점[n]으로부터 각 모든 지점의 최소 비용 갱신해나감
1) 비용 배열, 우선순위 큐 초기화
-
시작 지점
time[n] = 0, 나머지 지점은INF로 초기화 -
pq.add(시작 지점 n, 소비 시간 0) -
INF= 노드 최대 개수 (|n - k| 최대 10^5) x 간선 가중치 최대값 1 = 10^5
2) 우선순위 큐가 empty 할 때까지, 다음을 반복
-
비용 작은 순으로
pq에서 꺼냄
=> 해당 지점의 시간time[i]이 이미 갱신된 경우는 제외 -
꺼낸 현재 노드의 -1칸, +1칸, x2칸 3가지 다음 위치에 대해,
현재 노드를 거쳐서 다음 위치를 갈 때 비용이 더 적은 경우
=> 비용 갱신 및 우선순위 큐에 추가
2. 자료구조
-
int[] time: 다익스트라로 갱신할 가중치(시간) 배열
ex)time[10] = 5이면, 지점 10 을 5초 소비하여 방문
=> 자료형: 최대값 INF = 10^5 이므로, int 가능
=> 메모리: 4 x 10^5 byte = 0.4 MB -
PriorityQueue<Node>: 비용 가장 작은 노드부터 꺼냄
=>Node: 위치position, 소비 시간time
3. 시간 복잡도
- 다익스트라 시간 복잡도: O(E log_2 V)
=> 한 Edge 에 Vertex 3개 가정 (E = 3V)
=> O(3V log_2 V)
=> V = |n - k| => 최대값 10^5
=> (3 x 10^5) x log_2 10^5 = (15 x 10^5) x log_2 10
~= (15 x 10^5) x log_2 2^3 = 45 x 10^5 << 2억
코드
import java.io.*;
import java.util.*;
class Node implements Comparable<Node> {
public int position; // 현재 지점
public int time; // 소비 시간
public Node (int position, int time) {
this.position = position;
this.time = time;
}
public int compareTo(Node n) {
return this.time - n.time;
}
}
public class Main_Dijkstra {
static int n, k; // 수빈이의 시작 지점 n, 목표 동생 지점 k
static int minTime; // 출력, 최소 시간
static final int MAX_POSITION = 100_000;
static final int INF = 100_000;
static int[] time = new int[MAX_POSITION + 1];
static PriorityQueue<Node> pq = new PriorityQueue<>();
static void dijkstra() {
// 비용 배열, 우선순위 큐 초기화
Arrays.fill(time, INF);
time[n] = 0;
pq.add(new Node(n, 0));
while (!pq.isEmpty()) {
Node current = pq.remove();
// 이미 갱신된 time[] 은 제외
if (time[current.position] < current.time)
continue;
int np1 = current.position - 1;
// 현재까지 갱신된 최적 경로로 다음 지점 도달 최소 시간 time[np1]
// > 현재 새로 탐색하는 경로로 다음 지점 도달 시간 current.time + 1
if (isValid(np1) && time[np1] > current.time + 1) {
time[np1] = current.time + 1;
pq.add(new Node(np1, time[np1]));
}
int np2 = current.position + 1;
if (isValid(np2) && time[np2] > current.time + 1) {
time[np2] = current.time + 1;
pq.add(new Node(np2, time[np2]));
}
int np3 = current.position * 2;
if (isValid(np3) && time[np3] > current.time) {
time[np3] = current.time; // x 2 순간 이동은 시간 그대로
pq.add(new Node(np3, time[np3]));
}
}
}
static boolean isValid(int position) {
return 0 <= position && position <= MAX_POSITION;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in)
);
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
if (n >= k)
minTime = n - k; // -1 칸씩 n-k 번 이동하는 한 가지
else {
dijkstra();
minTime = time[k];
}
System.out.println(minTime);
}
}풀이 ② - BFS
1. 아이디어
-
목표 지점을 찾으면 탐색을 종료하는, 일반적인 DFS, BFS는 간선의 가중치가 모두 같아야 함.
하지만, 본 문제는 +1, -1 로 가는 경우 가중치가 1,
x2 로 가는 경우 가중치가 0 으로 가중치가 다름 -
BFS를 사용하되,
Queue에서 꺼낸 노드가 목표 지점일 때
BFS 탐색을 종료하지 않아야 함
=>Queue가 empty 할 때까지,Queue에 들어있는 노드를 모두 확인하여 탐색
- 방문 처리 배열을
boolean[]이 아닌,int[]사용
=> 해당 지점을 방문하는 최소 가중치(최소 시간)를 갱신해나가며 탐색
=> 현재 노드를 거쳐서 다음 위치를 갈 때 비용이 더 적은 경우,
최소 비용 갱신 및Queue에 다음 지점 노드를 추가 (BFS 탐색 확장)
2. 자료구조
-
Queue<State>,LinkedList<State>: BFS
=>State: 현재 지점position, 소비 시간time -
int[] visited: 방문 확인
ex)visited[10] = 5이면, 지점 10 을 5초 소비하여 방문
=> 메모리: 4 x 10^5 byte = 0.4 MB
3. 시간 복잡도
- BFS 의 시간 복잡도: O(V + E)
=> 한 Edge 에 Vertex 3개 가정
=> V + E = V + 3V = 4V = 4n
=> n 최대값 대입: 4 x 10^5 << 2억
코드
import java.io.*;
import java.util.*;
class State {
public int position; // 현재 지점
public int time; // 소비 시간
public State (int position, int time) {
this.position = position;
this.time = time;
}
}
public class Main_BFS {
static int n, k; // 수빈이의 시작 지점 n, 목표 동생 지점 k
static int minTime; // 출력, 최소 시간
static final int MAX_POSITION = 100_000;
static final int INF = 100_000;
static int[] visited = new int[MAX_POSITION + 1];
static Queue<State> queue = new LinkedList<>();
static void bfs() {
Arrays.fill(visited, INF);
visited[n] = 0;
queue.add(new State(n, 0));
while (!queue.isEmpty()) {
State current = queue.remove();
int np1 = current.position - 1;
// 현재까지 갱신된 최적 경로로 다음 지점 도달 최소 시간 visited[np1]
// > 현재 경로로 다음 지점 도달 시간 current.time + 1
if (isValid(np1) && visited[np1] > current.time + 1) {
visited[np1] = current.time + 1;
queue.add(new State(np1, visited[np1]));
}
int np2 = current.position + 1;
if (isValid(np2) && visited[np2] > current.time + 1) {
visited[np2] = current.time + 1;
queue.add(new State(np2, visited[np2]));
}
int np3 = current.position * 2;
if (isValid(np3) && visited[np3] > current.time) {
visited[np3] = current.time; // x 2 순간 이동은 시간 그대로
queue.add(new State(np3, visited[np3]));
}
}
minTime = visited[k];
}
static boolean isValid(int position) {
return 0 <= position && position <= MAX_POSITION;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in)
);
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
if (n >= k)
minTime = n - k; // -1 칸씩 n-k 번 이동하는 한 가지
else
bfs();
System.out.println(minTime);
}
}