백준 1789, 수들의 합 - Binary Search, Greedy

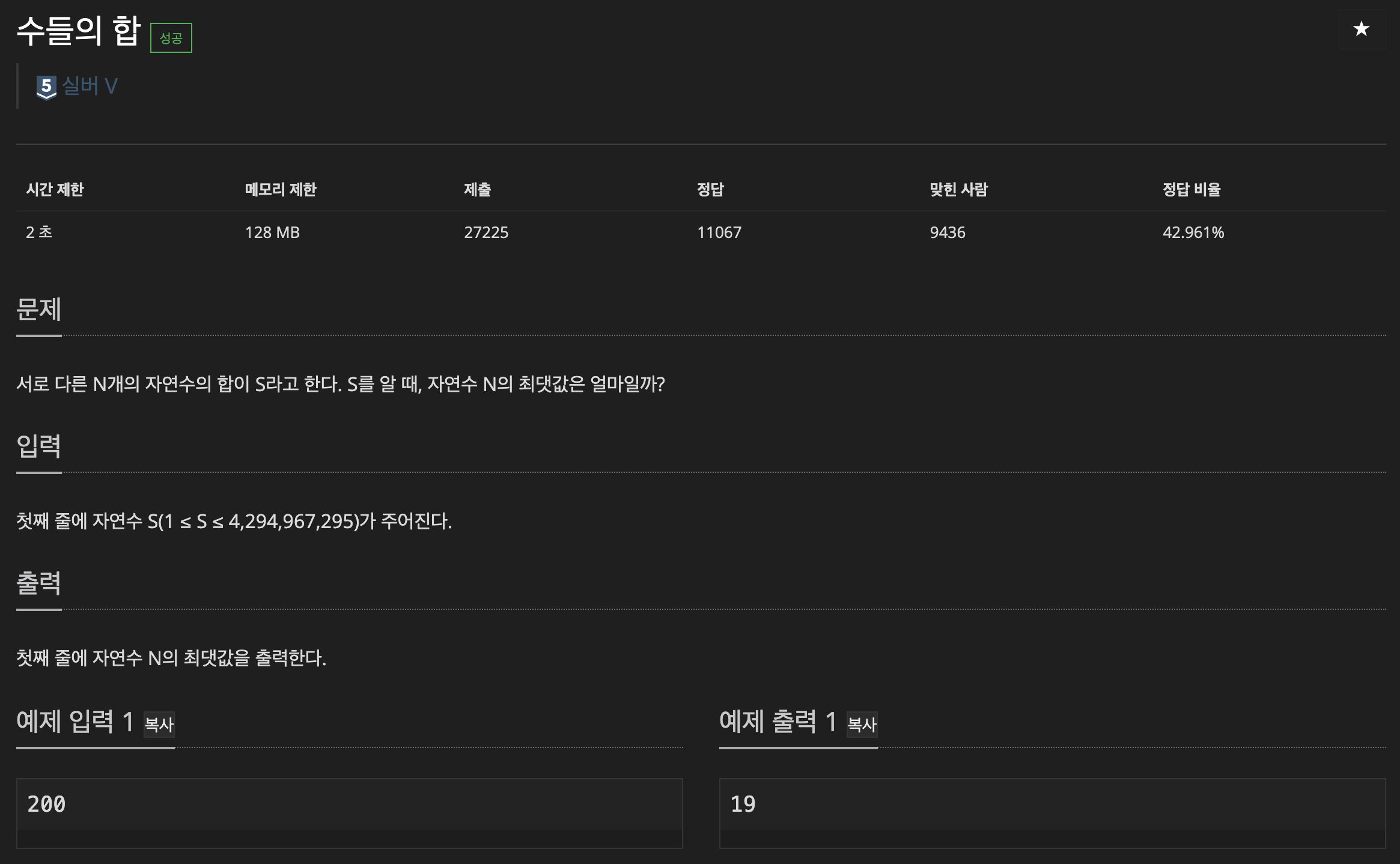
https://www.acmicpc.net/problem/1789

1. 아이디어

• 합 s 가 주어질 때, 자연수 개수 n이 최대가 되려면,
  합을 이루는 자연수 원소들의 값이 작은 순서로 구성되어야 함
  => 1, 2, 3, 4, ... 와 같이 정렬된 배열 형태

• 이진 탐색

  • 1 ~ end의 합과 목표 상한 합 s를 비교

  • Init Call: start = 1, end = s
    
    

1) 1 ~ mid 까지의 합 > 목표 합 s인 경우

• start = start, end = mid - 1로 다시 탐색

2) 1 ~ mid 까지의 합 < 목표 합 s인 경우

• 최대 자연수 개수 n 갱신
  => n = max(n, mid)

• start = mid + 1, end = end로 다시 탐색

3) 1 ~ mid 까지의 합 = 목표 합 s인 경우

• 탐색 종료, mid 반환 및 출력

2. 자료구조

• long s: 입력 자연수의 합
  => s > 21억 이므로, int 불가능하여 long 사용

3. 시간 복잡도

• 이진 탐색 시간 복잡도: O(log_2 n)
  => 탐색 범위 s 최대값 대입: log_2 2^32 = 32 << 2억

코드

import java.io.*;

public class Main {
	static long s;
	static long n;			// 출력, 최대 자연수 개수

	static void binarySearch(long start, long end) {
		if (start > end)
			return;

		long mid = (start + end) / 2;
		long sum = calcSum(mid);			// 1 ~ mid 까지의 합
		if (sum > s) {
			binarySearch(start, mid - 1);
		}
		else if (sum < s) {
			n = Math.max(n, mid);
			binarySearch(mid + 1, end);
		}
		else {
			n = mid;
			return;
		}
	}

	/* 1 ~ x 의 합 계산 */
	static long calcSum(long x) {
		return (x * (x + 1)) / 2;
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(
				new InputStreamReader(System.in)
		);

		s = Long.parseLong(br.readLine());

		binarySearch(1, s);
		System.out.println(n);
	}
}