백준 20115, 에너지 드링크 - Greedy

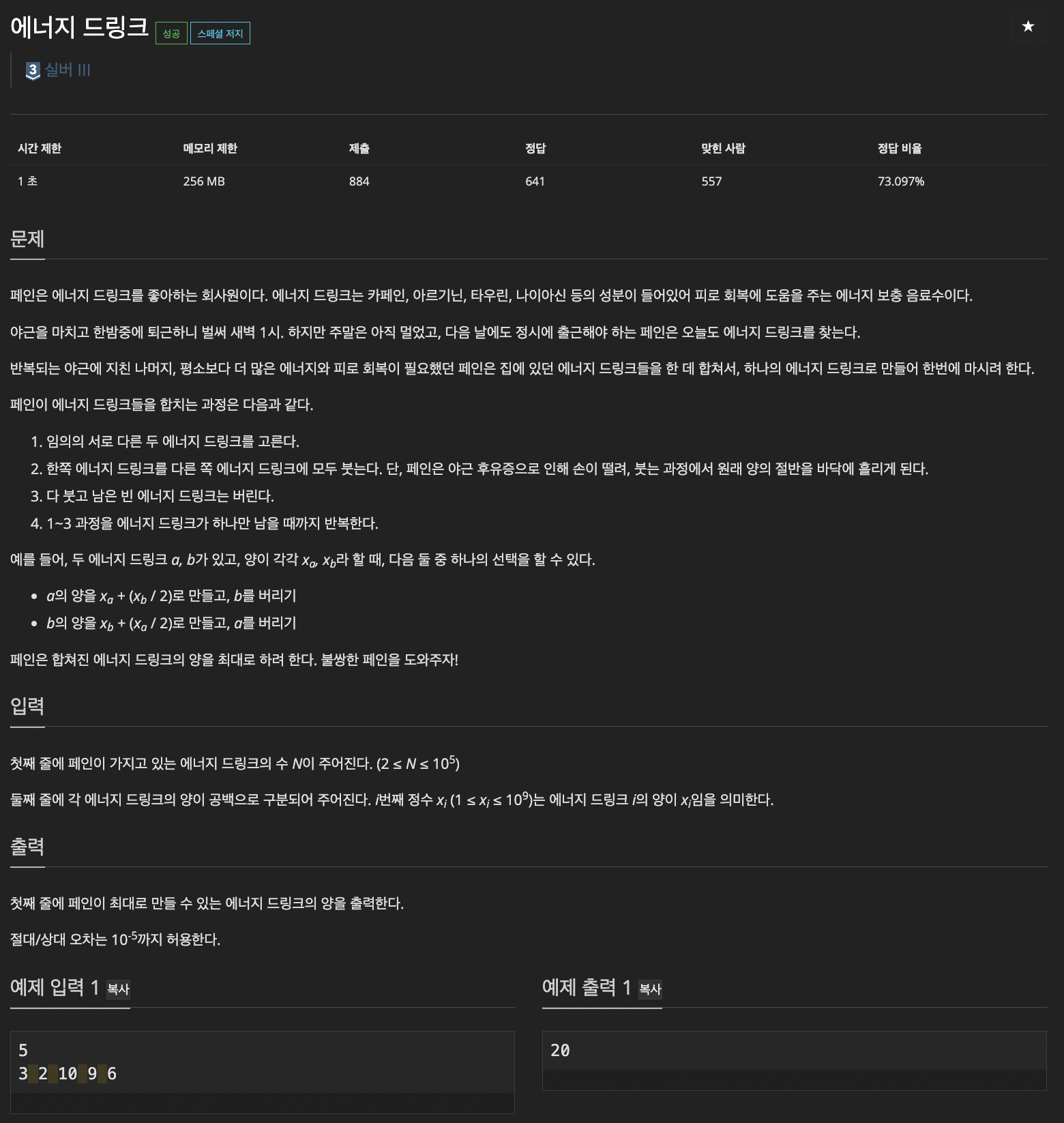
https://www.acmicpc.net/problem/20115

1. 아이디어

• 규칙에 따라 합친 최종 에너지 드링크의 양을 최대로 만들기
  => 절반을 버리고 합치므로, 절반을 버리는 드링크는 양이 작아야 함

• 규칙: 가장 작은 양의 드링크의 절반을 가장 큰 양의 드링크에다 부어서 합치기
  => 가장 큰 양의 드링크가 계속 늘어나면서 갱신됨

1) 드링크 양 배열을 작은 순으로 정렬
2) 가장 큰 양(배열의 맨 뒤 원소)을 선택하여, 맨 앞의 작은 양부터 차례로 합쳐나감

2. 자료구조

• int[] amounts: 각 드링크의 양
  => 작은 순으로 정렬 후, 맨 앞의 가장 작은 양부터 선택하여 가장 큰 양에 더해나감

3. 시간 복잡도

• 배열 정렬: O(n log_2 n)

• 드링크 합치기: O(n)

=> 전체 시간 복잡도: O(n + n log_2 n)
=> n 최대값 대입: 10^5 + 10^5 x log_2 10^5 = 10^5 + (5 x 10^5 log_2 10)
~= 10^5 + (15 x 10^5) = 16 x 10^5 << 1억

코드

import java.io.*;
import java.util.*;

public class Main {
	static int n;					// 전체 드링크의 수
	static int[] amounts;			// 각 드링크의 양
	static double maxAmount;		// 합쳐지면서 갱신되는 드링크 최대 양

	static void solution() {
		Arrays.sort(amounts);
		maxAmount = amounts[n - 1];

		for (int i = 0; i <= n - 2; i++)
			maxAmount += (double) amounts[i] / 2;
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(
				new InputStreamReader(System.in)
		);
		StringTokenizer st;

		n = Integer.parseInt(br.readLine());
		amounts = new int[n];

		st = new StringTokenizer(br.readLine());
		for (int i = 0; i < n; i++)
			amounts[i] = Integer.parseInt(st.nextToken());

		solution();
		System.out.println(maxAmount);
	}
}