백준 2437, 저울 - Greedy, 누적 합

https://www.acmicpc.net/problem/2437

1. 아이디어

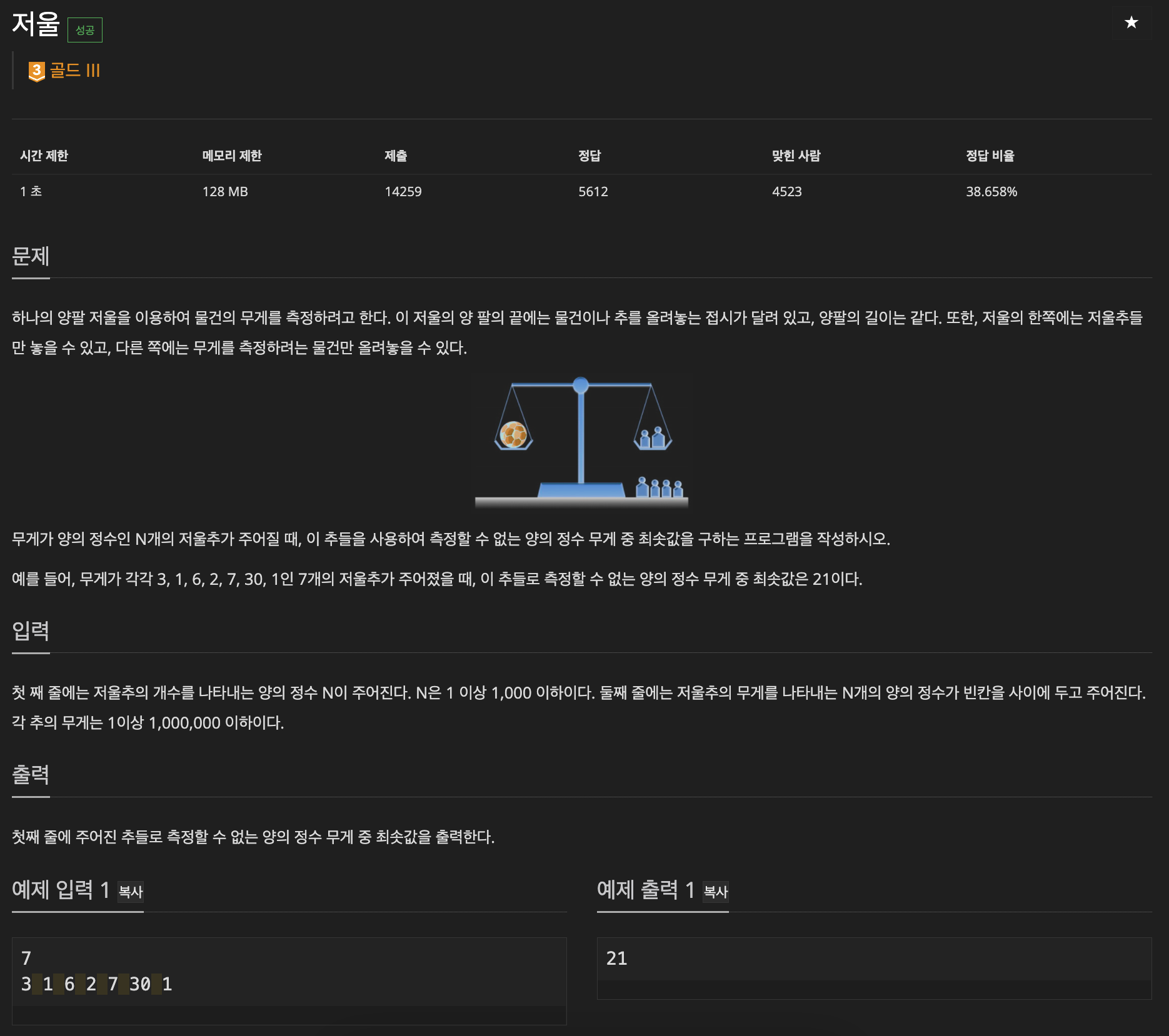
• n개의 추들의 조합으로 만들 수 없는 최소 무게 구하기
  ① n개 추들의 조합으로 만들 수 있는 "최대 무게" = 모든 추들의 무게 합
  ② n개 추들의 조합으로 만들 수 없는 "최대 무게" = 모든 추들의 무게 합 + 1
  ③ 작은 무게 ~ 큰 무게 순으로 정렬했을 때,
  인접한 추 끼리 무게 차이가 작아야 더 촘촘히(?) 추의 무게 합 구성 가능
  
  

• n개 추들을 무게 작은 순으로 정렬

①에서 유추한 규칙

• 가장 가벼운 [0]번째 추 ~ [i]번째 추 까지의 무게 누적합
  = [0]번째 추 ~ [i]번째 추들의 조합으로 만들 수 있는 최대 무게

②, ③에서 유추한 규칙

• ([0]번째 추 ~ [i]번째 추 까지의 무게 누적합 + 1) < 다음 [i+1]번째 추의 무게인 경우
  => ([0]번째 추 ~ [i]번째 추 까지의 무게 누적합 + 1) 무게 구성 불가능

2. 자료구조

• int[]: 각 추들의 무게

3. 시간 복잡도

• 배열 정렬: O(n log_2 n)
  => n 최대값 대입: 10^3 log_2 10^3 = 3 x 10^3 log_2 10 ~= 9 x 10^3

• 누적합 더해가며 무게 구성 여부 확인: O(n)
  => n 최대값 대입: 10^3

=> 전체 시간 복잡도: O(n + n log_2 n)
=> n 최대값 대입: (9 x 10^3) + 10^3 = 10^4 << 1억

코드

import java.io.*;
import java.util.*;

public class Main {
	static int n;				// 추 개수
	static int[] weights;		// 각 추의 무게
	static int minSum;			// 출력, 입력 추 조합으로 만들 수 없는 최소 무게 합

	static void solution() {
		int sum = 0;			// 추 무게 누적합

		for (int i = 0; i < n; i++) {
			// ([0]번째 추 ~ [i]번째 추 까지의 무게 누적합 + 1) < 다음 [i+1]번째 추의 무게인 경우
			// ※ 최초 누적합(sum = 0) + 1 = 1 < weights[0] 비교하여, 무게 1 만들 수 있는지 확인
			if (sum + 1 < weights[i]) {
				// ([0]번째 추 ~ [i]번째 추 까지의 무게 누적합 + 1) 무게 구성 불가능
				minSum = sum + 1;
				return;
			}

			sum += weights[i];
		}

		// [0]번째 추 ~ [n-2]번째 추 까지의 무게 누적합을 구성 가능한 경우
		// => (모든 추의 무게 누적합 + 1) 무게 구성 불가능
		minSum = sum + 1;
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(
				new InputStreamReader(System.in)
		);
		StringTokenizer st;

		n = Integer.parseInt(br.readLine());
		st = new StringTokenizer(br.readLine());

		weights = new int[n];
		for (int i = 0; i < n; i++)
			weights[i] = Integer.parseInt(st.nextToken());

		Arrays.sort(weights);

		solution();
		System.out.println(minSum);
	}
}