
요새 노마드 코더 채널에서 니꼴라스가 10분씩 알고리즘 및 자료구조를 정리해주는데
간단하게 정리할 겸 적어보려 한다.
Array 배열
Time Complexity(시간복잡도)
데이터 구조의 오퍼레이션 혹은 알고리즘이 얼마나 빠르고 느린지 측정하는 방법
실제 시간을 측정하는 것이 아니라 얼마나 많은 단계 steps가 있는 지로 측정
단계가 적을 수록 좋다 :)
2가지 종류의 메모리
volatile(휘발성) vs non-volatile(비휘발성)
메모리 RAM vs 컴퓨터를 껐다 켜도 데이터가 남아있는 하드 드라이브
프로그램이 돌아가고 변수를 생성할 때 등 모든 건 RAM(Ramdom Access Memory) 에 저장
하드메모리의 데이터를 읽는 것 보다 RAM에 있는 데이터를 읽는 게 빠르다
RAM을 박스 그룹이라고 가정한다.
그 박스들은 데이터를 저장할 수 있고 박스의 이름이 memory address 다.
프로그램이 RAM 메모리에게 memory address로 가고싶다고 하면 바로 접근이 가능하다.
바로 해당 어드레스로 이동할 수 있다.
메모리 관점에서의 배열
배열을 만들 때 컴퓨터에게 배열의 길이만큼 공간을 미리 예약/할당 해야한다.
메모리 안에 박스들이 나란히 자리할 수 있도록.
JS, python 은 배열을 선언할 때 length 를 직접 정하지 않지만 백그라운드에서 이 과정을 다 해주고 있는 것이다.
Reading
배열은 0부터 인덱싱을 한다. 위치만 알면 배열의 데이터에 접근할 수 있다.
컴퓨터는 배열이 어디서 시작하는 지 알고 있기 때문에 read 가 빠르다.
길이와 상관없이 인덱스에서 요소를 읽어내는 속도는 동일하기 때문에 많은 양의 자료를 읽을 때 유리하다.
searching
reading과 searching 은 다르다.
찾고 싶은 값이 배열에 있는지, 없는지, 어디에 있는지 모른다.
배열의 요소를 하나씩 체크해야 한다. one by one
최선의 경우: 찾는 값이 첫번째 인덱스에 있는 것
평균의 경우는 중간에 있는 것
최악의 경우는 맨 마지막 인덱스에 있는 것, 진짜 최악은 없는 것...
배열에서 searcing은 빠르지 않다.
선형 검색 Linear searching: 순서대로 0부터 끝까지 찾는 것
insert(add)
배열을 만들 때 메모리 공간을 미리 확보해야 한다.
"어디에" 새 값을 추가할 것인가.
최고의 경우 : 그 값을 배열 맨 끝에 추가하는 경우, 컴퓨터는 배열이 어디서 시작하고 얼마나 긴 지 알고 있기 때문에 배열의 맨 끝으로 이동하여 새 값을 추가하는 건 빠르다.
평균의 경우 : 배열 중간에 추가하는 경우
최악의 경우 : 배열의 맨 앞에 추가하는 경우, 모든 요소를 한 칸 씩 움직여야 한다.
따라서 배열의 크기가 크면 클 수록 위치에 따라 insert 가 오래걸릴 수 있다.
또 다른 경우는 이미 공간이 꽉찼는데 값을 추가하려고 하는 경우이다. 이런 경우는 새 배열을 만들어서 이전 배열을 복사하고 추가해야하기에 시간이 오래 걸린다.
delete
삭제는 삽입과 비슷하다.
최고의 경우 : 마지막 값을 삭제할 때
평균의 경우 : 중간 값을 삭제할 때
최악의 경우 : 맨 앞의 값을 삭제할 때, 맨 앞의 공백을 없애기 위해 모든 요소가 한 칸 씩 움직여야 한다.
삽입과 마찬가지로 배열이 길면 길 수록 오래 걸리게 된다.
배열은 read가 빠르고 searcing, adding, deleting 이 느리다.
추가, 삭제를 하고 싶을 경우에는 배열 맨 끝에서 작업하는 것을 추천한다.
검색 알고리즘
배열 안에 잇는 숫자를 어떻게 찾을 수 있는 지
어떤 알고리즘을 선택하느냐에 따라 스피드가 어떻게 달라지는지를 알아보자
완벽한 자료구조, 알고리즘 조합을 찾아내면 코드의 스피드 자체가 달라진다.
알고리즘에도 Time Complexity (시간 복잡도) 가 존재한다
Linear Search (선형검색 알고리즘)
가장 자연스러운 방법
순서대로 처음부터 끝까지 검색하는 방법
최악의 경우 : 배열 맨 마지막에 있거나 아예 없는 경우
배열이 길어질 수록 검색 시간도 오래걸린다 = Linear Time Complexity
Sorted Array
정렬이 안된 배열에 요소를 추가하는 건 쉬우나 정렬된 배열에 요소를 추가하는 건 오래걸린다.
이유는 해당 배열에서 요소보다 큰 값을 찾은 후 값을 다 한 칸 씩 이동한 후에 큰 값 왼쪽에 삽입해야하기 때문
Binary Search (이진검색 알고리즘)
정렬된 배열(Sorted Array) 에서만 사용가능
이진 => 반으로 쪼개다
인덱스 0 부터 검색하지 않고 middle(중간) 부터 검색을 시작한다.
1. 가운데 숫자가 target 보다 큰 지, 작은 지 비교
2. n > target : target은 n의 왼쪽에 위치, n < target : target은 n의 오른쪽에 위치
3. 왼쪽 또는 오른쪽 배열의 중간값과 target을 다시 비교
4. 반복 하다가 target을 찾는다!이진 검색은 매 스텝마다 절반의 아이템을 없애기 때문에 배열의 길이가 길어져도 작업을 수행하는데 필요한 스텝이 선형적으로 늘어나지 않는다.
따라서 이진검색은 거대한 배열을 다룰 때 효과적이다.
그러나 이진검색을 하고싶다면 배열을 정렬해야 한다. 이는 새 요소를 추가에 시간이 오래걸린다.
이러한 상충관계를 잘 알고 적절한 자료구조, 알고리즘을 사용해야 한다.
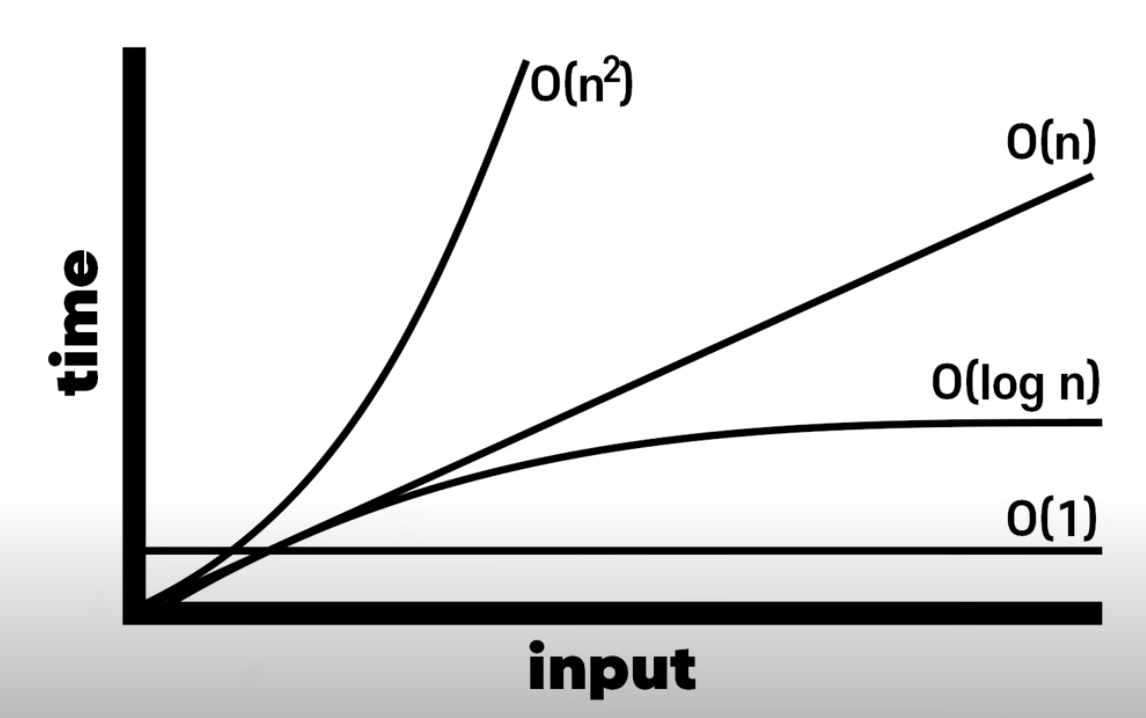
Big O
빠른 알고리즘은 느린 알고리즘보다 우수하다.
알고리즘의 스피드를 나타내는 방법 : 완료까지 걸리는 절차의 수 => Big O
상수 시간 시간복잡도
def print_first(arr):
print(arr[0]);input size 에 상관없이 1step이면 끝난다.
이 함수의 시간복자도는 constant time (상수시간)이다.
=> O(1)
프린트를 두번 한다면 O(2) 인가?
=> NO. O(1)
BigO는 함수의 디테일엔 관심이 없고 인풋사이즈에 따라 함수가 어떻게 동작하는지만 관심이 있기 때문에 여전히 O(1)이다. 상수 시간인 경우에는 그 step이 200이든 5이든 O(1)이다. 그래프가 같기 때문에 러프하게 O(1)로 표시한다.
O(n)
-
선형 검색 알고리즘의 경우
input size = n
algorithm steps = n steps
=> complexity : O(n) -
반복문
def print_all(arr):
for n in arr :
print(n)=> O(n)
반복문이 두개라면? O(2n)?
=> No. O(n)
O(n^2)
시간복잡도의 Quadratic time(2차 시간)
2차 시간은 Nested Loop(중첩 루프)에서 발생
O(log n)
로그(logarithm) <-> 지수(exponent)



n을 구하는 방법은 32를 2로 나눴을 때 1이 나오기 까지의 step 을 구하는 방법과 동일하다
32/2 = 16
16/2 = 8
8/2 = 4
4/2 = 2
2/2 = 1
총 5번 이기 때문에 n = 5 가 된다.
이 방법은 이진검색 방법과 매우 비슷하다.
따라서 정렬된 배열의 이진검색의 시간복잡도는 O(log n)이다.
Sorting 정렬 알고리즘
항상 BigO가 모든 알고리즘을 완벽하게 설명하는 것은 아니다.
같은 BigO를 가지고 있어도 각각의 퍼포먼스가 다를 수 있다.
sorting 이란
무언가를 정리하는 것, 정렬하는 것.
버블 정렬 Bubble Sort
배열의 2개의 아이템을 선택하고 비교 -> 값이 큰 쪽을 오른쪽으로 가도록 교환, 이를 반복한다.
버블정렬의 시간복잡도는?
사이클마다 n-1 번 비교, 최악의 경우 모든 사이클을 n-1 번 비교해야한다.
따라서 O(n^2), 좋은 알고리즘이 아니다.
선택 정렬 Selection Sort
전체 아이템 중 가장 작은 아이템의 위치를 변수에 저장한다.
그 다음 첫번째 아이템과 가장 작은 아이템의 위치를 교환한다.
그러면 제일 첫번째 아이템은 정렬된 부분이고 정렬되지 않은 부분 중 가장 작은 아이템을 찾고 위의 과정을 반복한다.
선택정렬의 시간 복잡도는?
정렬되지 않은 전체 배열에서 가장 작은 숫자를 찾으므로 n-1 비교를 한다.
하지만 버블정렬과 다르게 최악의 경우에도 n번의 스왑을 하지않는다.
한 사이클에서 1 번의 스왑만 하면된다. (제일 작은 수만 앞으로 옮기면 됨)
따라서 시간은 버블정렬 > 선택정렬 버블정렬이 훨씬 많이 걸린다.
그러나 시간복잡도는 동일하게 O(n^2)
삽입 정렬 Insertion Sort
index 0 자리에 가장 작은 값을 넣어야 한다고 선택하면 그 왼쪽의 아이템부터 비교를 시작하여 작은 값을 발견하면 index 0 과 swap 한다.
index 0 의 왼쪽은 없으니까 index 1 부터 시작하고 key 값은 1이다.
삽입 정렬은 필요한 아이템만 스캔하여 비교하기 때문에 선택 정렬보다 빠르다.
그렇지만 시간복잡도는 동일하게 O(n^2)이다.
이 경우에는 최악의 시나리오만을 보지않고 평균 시나리오를 봐야한다.
insertion sort 는 Best scenario 가 O(n) 이고 나머지는 O(n^2)이다.
Hash Table
베리베리베리 임포턴트!
Hash table 과 Array 를 비교
array의 경우 요소를 찾기 위해서는 선형검색을 해야한다. 시간이 오래걸림. O(n)
hash table의 경우 key를 사용하여 value 를 바로 가져올 수 있다. 시간이 빠름. O(1)
검색 및 추가, 삭제도 O(1)
Array 대신 Hash Table을 사용하기
//array
fruits = ['사과', '배', '참외', '딸기']
//hash table
fruits = {
'사과' : true,
'배' : true,
'참외' : true,
'딸기' : true
}array를 사용해서 참외가 fruits 에 있는 지 확인하려면 하나씩 검색해서 찾아야 한다.
하지만 hash table을 사용하면
fruits['사과'] === true ? "있다" : "없다
이렇게 바로 검색하여 찾을 수 있다. 시간이 훨씬 빠르다.
Hash Table은 내부에 array가 있다.
하지만 array보다 빠르다. 그 이유는 hash function 때문이다!
Hash Function
Hash Function 이 key를 숫자로 바꿔버린다. 그 key 가 index가 되고 그 value에 내가 저장한 value 가 저장되는 것이다.
즉, hash function으로 hash table을 만든다고 하면 key를 해시함수에 넣고 반환된 숫자(index)에 value를 저장하면 된다.
hash function에 다른 key를 넣었는데 같은 숫자를 반환하면 어떻게 될까?
이를 해시 충돌(hash collision) 이라고 한다.
대처 방법. 리스트의 같은 숫자 공간에 또 다른 배열을 넣는다.
key 를 사용해서 value를 찾을 때 해시 함수에서 반환된 index 에 있는 요소에 배열이 있다면 그 곳에서 선형 검색을 하게 되는 것이다.
이 이유 때문에 언제나 해시 테이블의 검색 시간 복잡도가 O(1)이 아니다.
