회귀 트리 개념이 궁금해져서 따로 찾아보고 이해했었던 내용을 복습차 적어둔다.
StatQuest 님의 설명영상인데, 정말 정말 깔끔하다,,,
(출처 : https://www.youtube.com/watch?v=g9c66TUylZ4)
문제상황
- 감기를 치료하는 신약을 개발했는데, 최적의 투약량을 모르는 상태..
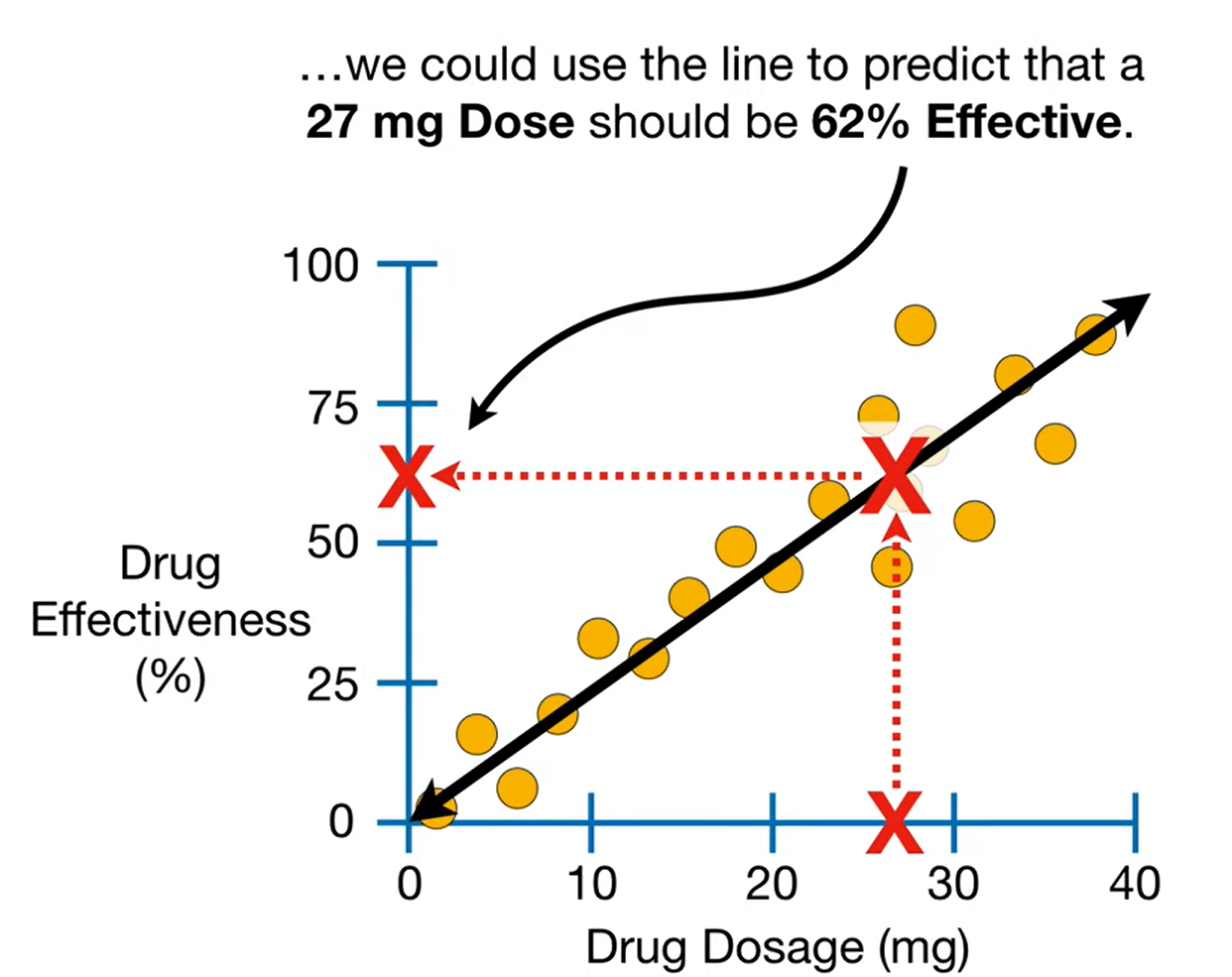
→ 투약량(x)을 다르게 설정해가며 약효(y)를 테스트해보았다. - 만약 결과가 아래처럼 나왔다면, 투약량과 약효의 관계를 선형적으로 볼 수 있고
새로운 샘플에 대한 예측도 쉽게 할 수 있다.
- 근데 만약 이런 식으로 결과가 나왔다면, 선형적인 예측은 매우 부정확해진다.
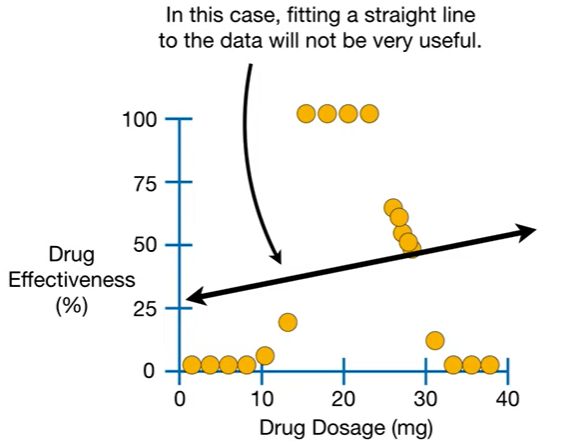
- 따라서 선형적인 예측모델 말고 다른 방법을 찾아야한다.
➡️ 그 중 하나가 바로 '회귀 트리(Regression Tree)'!!
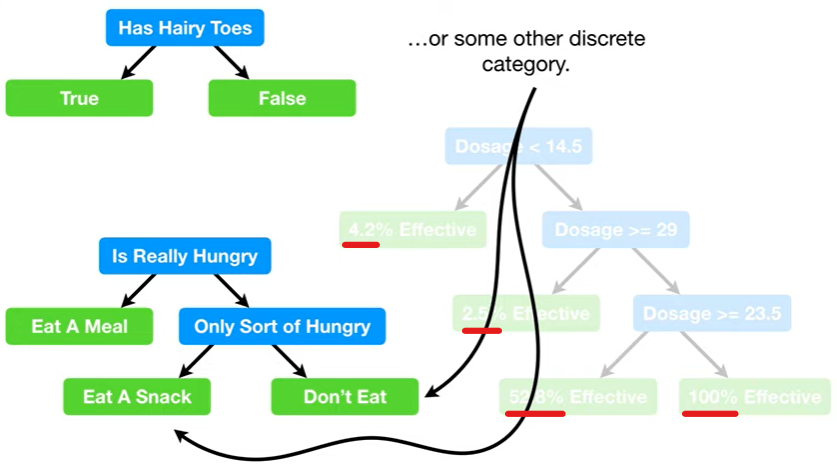
- 분류 트리(Classification Tree)는 각 리프에 T/F 또는 특정 카테고리 있었던 반면, 회귀트리는 숫자값(numeric values)이 들어있다는 특징이 있다.
회귀트리 읽기
- 자 읽단 읽는 법은 쉽다. 그냥 트리 따라 내려가면서 보면 된다. 위에서 부정확했던 선형 예측보다 확실히 정확도가 높다.
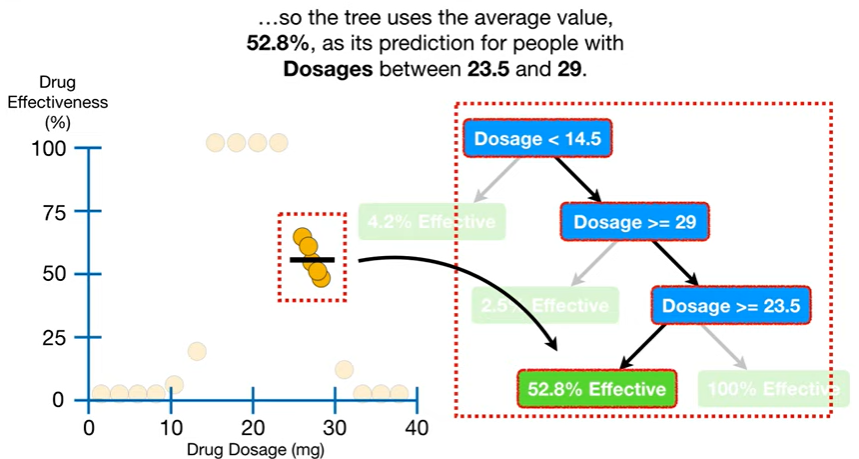
👨🏻🏫 그런데 누군가는 이렇게 물을 수도 있다. "근데 그건 그래프만 봐도 되는 거잖아요??" → 맞다. 이를테면, 투약량이 27일 때 약효가 50 정도라는 사실은
그래프만 봐도 바로 판단할 수 있다. 그렇다면 트리가 왜 필요한 걸까?
➡️ 사실 이건 간단한 예시인데, 실제로 더 다양한 독립변수(predictor)들이 추가되면 그래프로 그리는 것은 매우 힘들어진다. 하지만, 결정트리는 그런 복잡한 상황에서도 매우 직관적인 예측모델이 되어준다는 것!! 🆗

회귀트리 만들기
그럼 이 트리모델을 어떤 기준으로 어떻게 만들어나가는 걸까?
- 먼저 맨 위의 루트노드가 왜
Dosage<14.5인지부터 살펴보자.
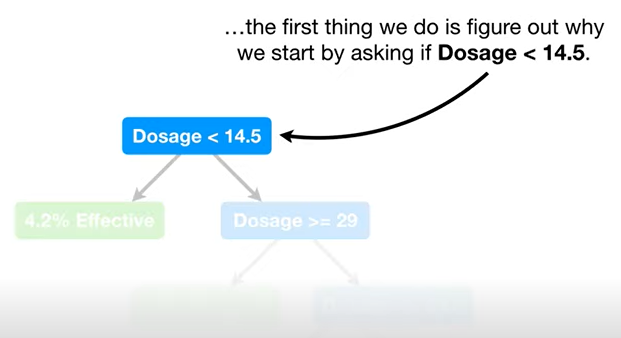
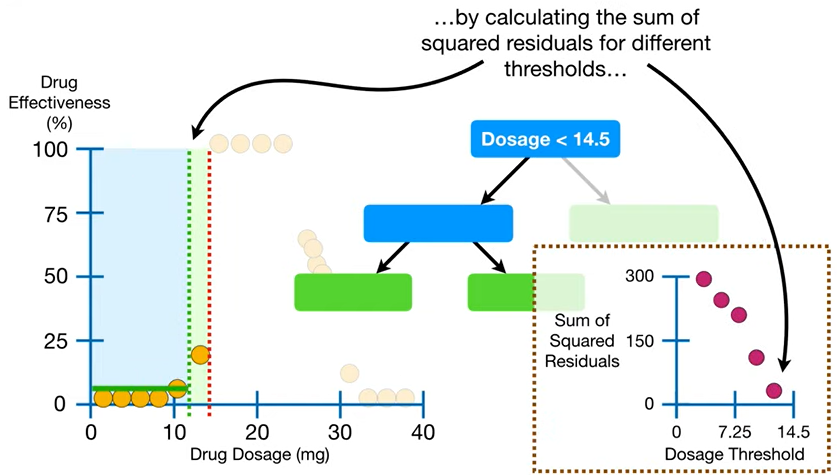
- ☝🏻일단 임의로, 맨 왼쪽 점(값) 두 개를 기준으로 끊어서 트리를 구성해보면,
(= 맨 왼쪽 2개의 값만 있다고 생각하고 그은 빨간색 구분선)
- 왼쪽 리프는 잘 들어맞는데, 오른쪽은 성능이 형편없다;;
→ 점선 그어보면 그 오차들을 볼 수 있고, 이걸 잔차(residual)라고 한다.
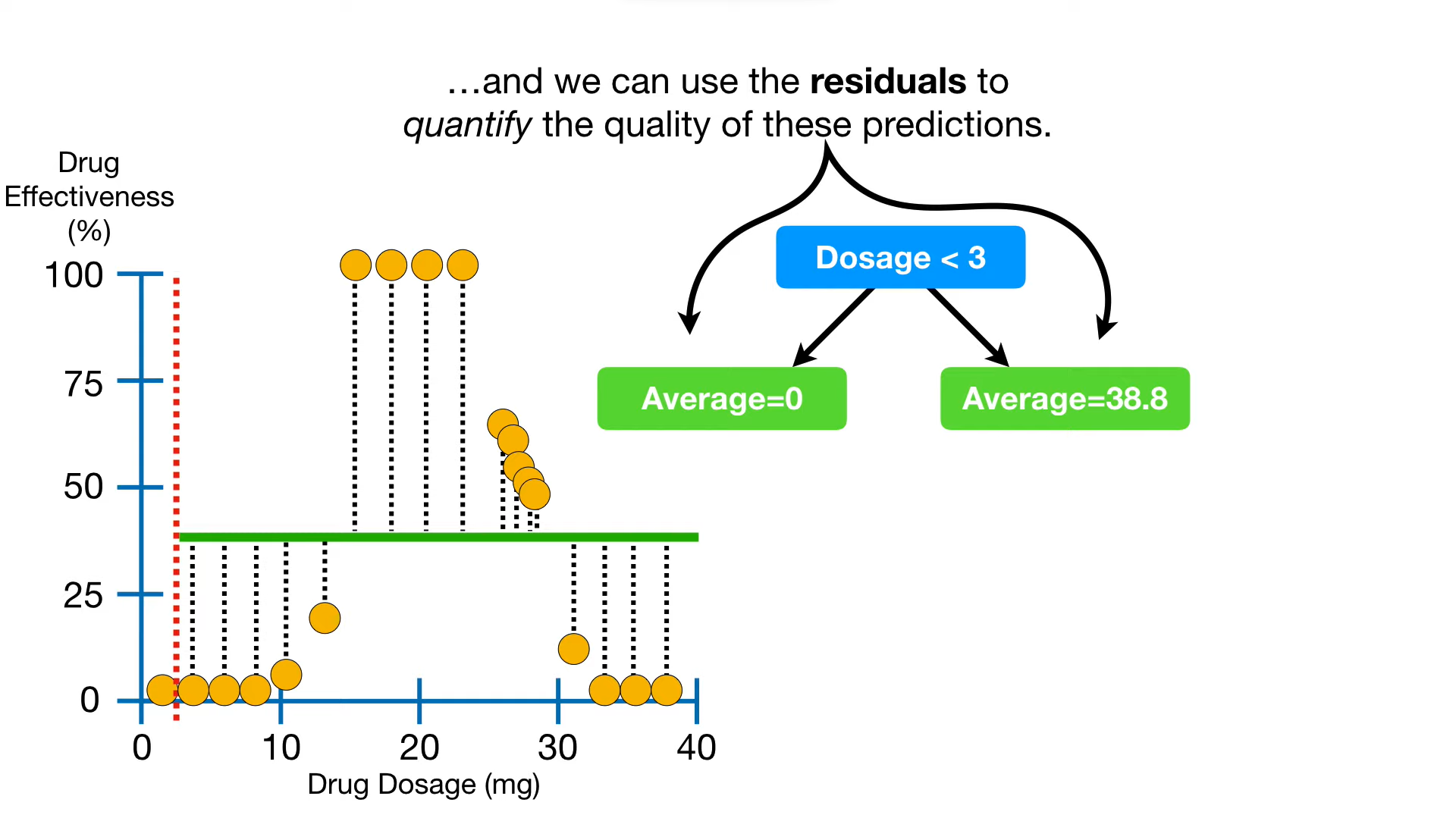
- 그 잔차의 총량은 제곱합으로 구할 수 있고,
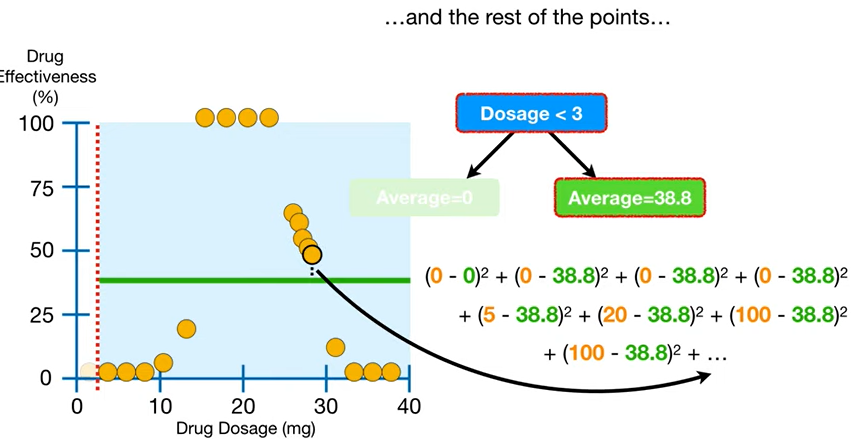
- 그렇게 구한 잔차의 제곱합(=잔차의 총량)을, 다른 그래프 하나에 따로 표시해두자.
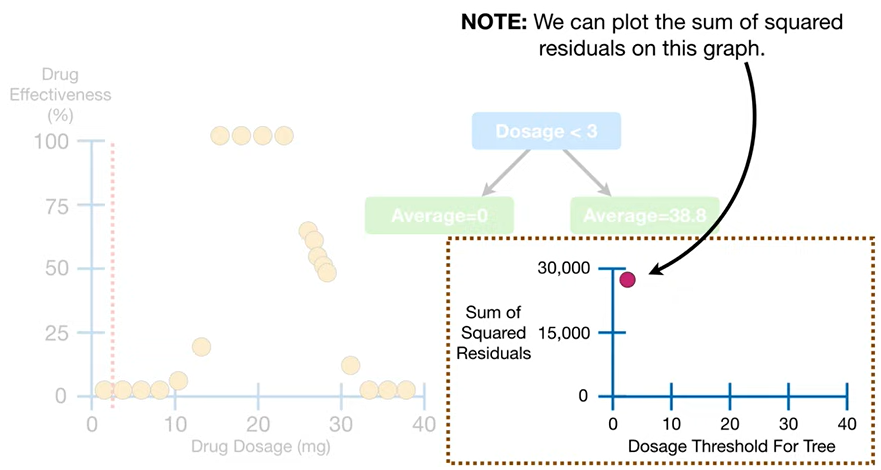
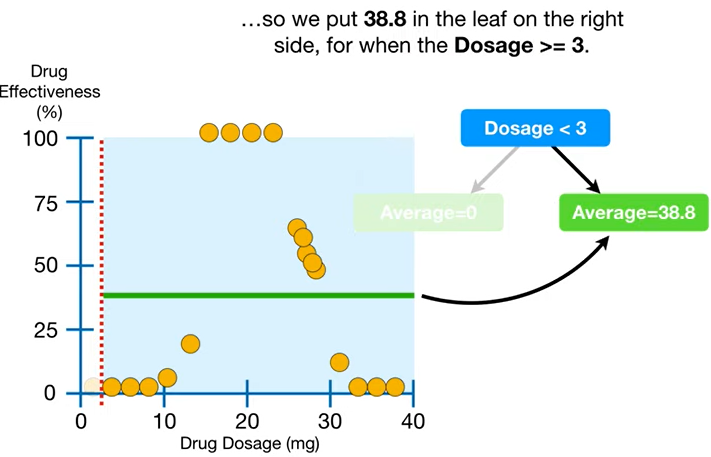
- ☝🏻자 이번엔, 왼쪽부터 2번째 & 3번째 점을 기준으로 끊고, (= 빨간 구분선 한칸 옆으로)
방금 했던 것처럼 임의의 트리 구성 + 잔차제곱합 계산하는 위 과정을 똑같이 해보자.
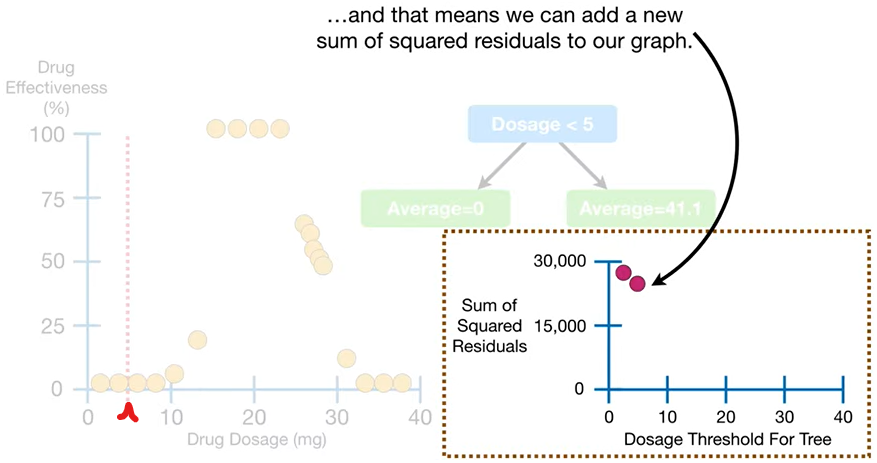
- 이렇게 계속 threshold(빨간 구분선)를 다르게 해가면서,
임의로 구성해본 각 트리들의 잔차제곱합을 모두 그래프에 찍어보면,
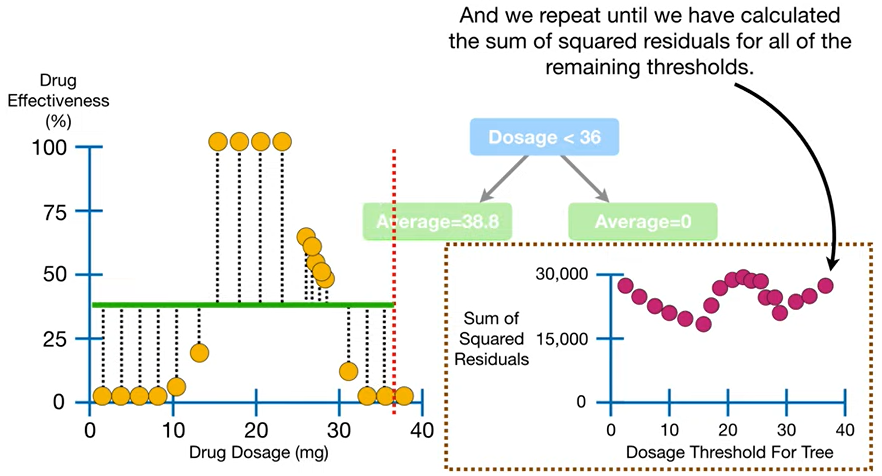
- 투약량(
Dosage)이 14.5 일 때 잔차제곱합이 제일 낮다는 걸 확인 가능!
= 제일 오차가 적네 = 제일 성능 괜찮네!
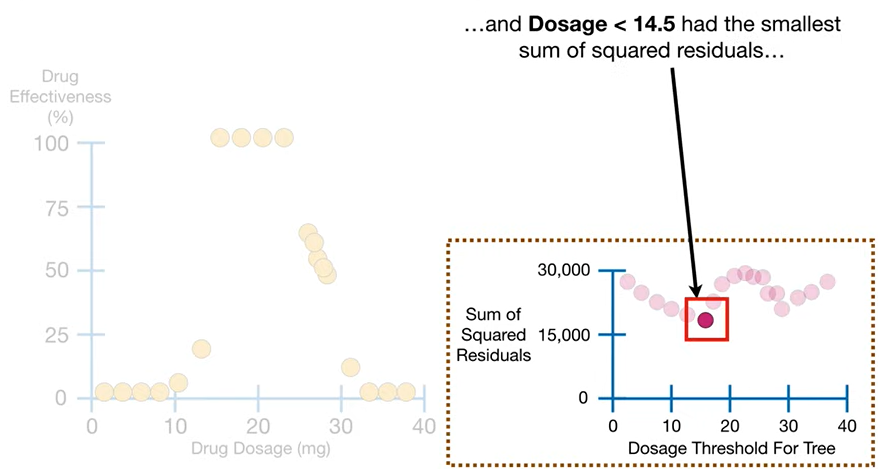
- 그래서
Dosage<14.5가 맨 위의 루트노드로 들어가는 것이다!!
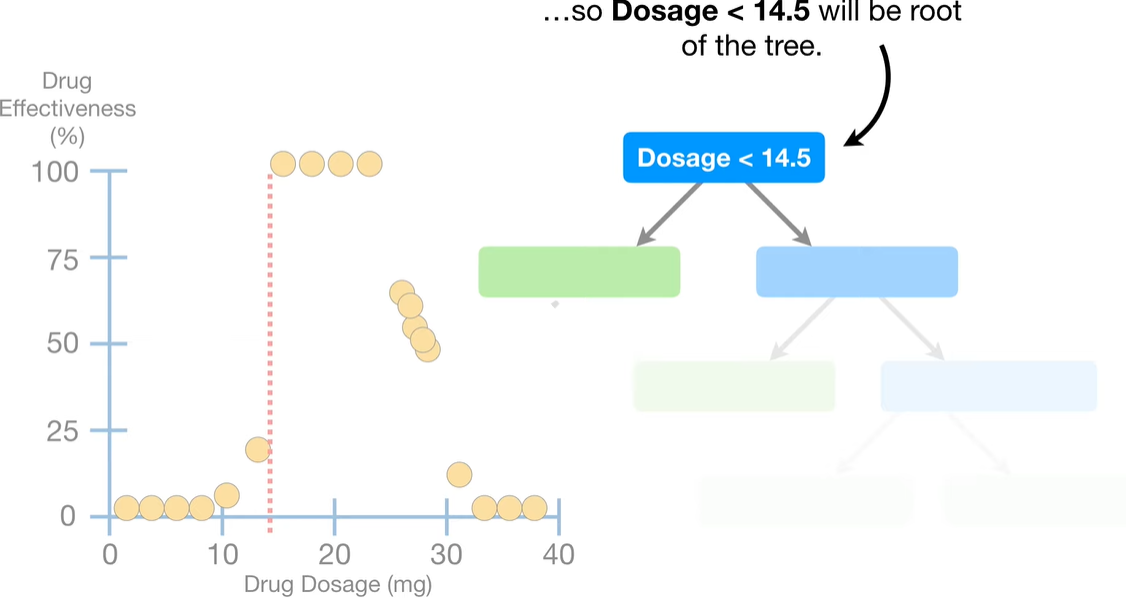
- ☝🏻자 그러고나서, 한 층 내려가면 또 두개씩 나눌 수 있다 = 또 위에서 했던
'최적의 threshold 찾기' 과정을 반복할 수 있다!
- 참고로, 아래처럼 값이 한 개만 남아서 더 쪼개지 못하는 노드를 리프 노드라고 한다.
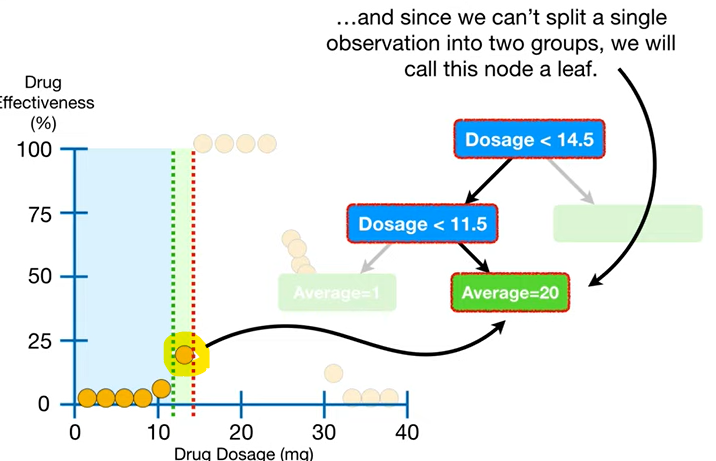
- 그리고 이렇게 다 같은 값으로 남게 된 경우도 더 쪼갤 필요가 없게 된다.
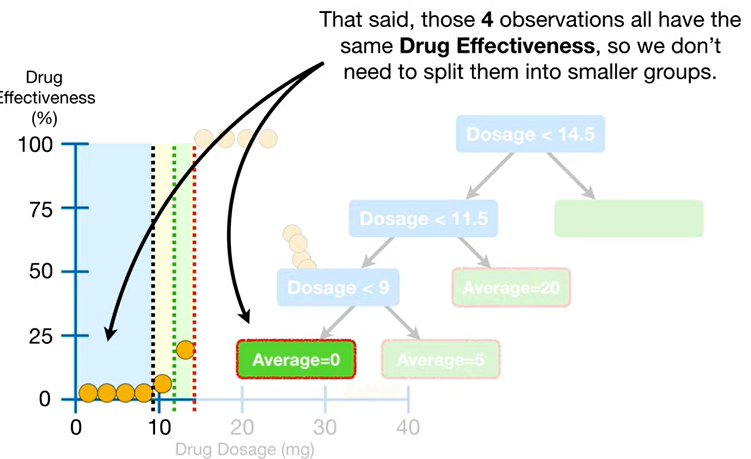
- ☝🏻"이런 식으로 트리를 만들어나가니까 루트노드의 왼쪽 부분은 완성됐다! 어느 점을 찍어서 트리를 따라가봐도, 다 완벽히 정확한 값을 예측한다!"
➡️ 근데 이게 결코 좋은 게 아니다...ㅠ 너무 훈련세트에만 잘 맞는 과대적합..!!;;
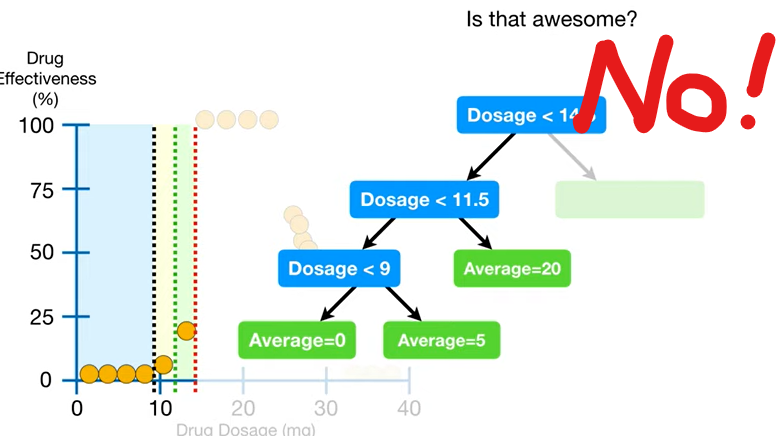
- "해결방법이 있나요?" 👨🏻🏫 "Yes"
- 과적합을 방지하는 가장 간단한 방법은 남겨놓을 minimum 개수를 설정하는 것!
= 트리를 과도하게 성장시키지 않고 일정 깊이로 제한하는 것 (보통 20개 정도)
ex) 만약 7개로 설정했다 치면, 아래처럼 2층에서 리프노드로 끝내버린다^^
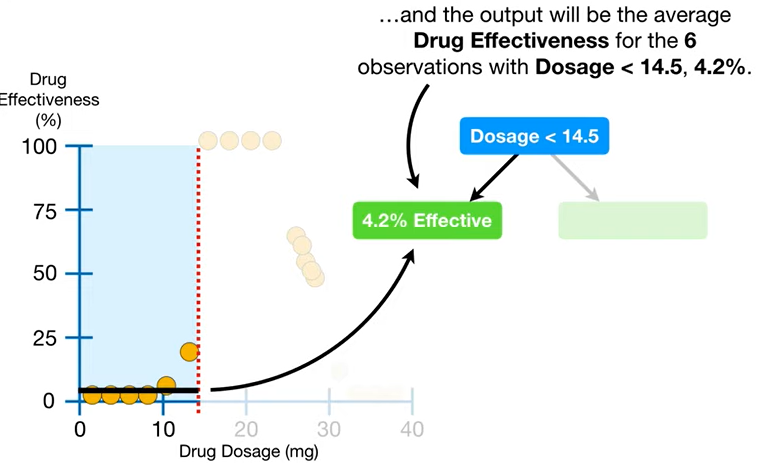
- ☝🏻자 그럼 이제,
Dosage<14.5의 오른쪽 부분을 보자.
(방금 minimum으로 설정한 7개보다 관측값이 더 많이 있으니 나눠도 됨 ㅇㅇ) - 위에서 했던 방식 그대로 최적의 threshold 찾으니까
Dosage>=29에서 한번 나뉜다.
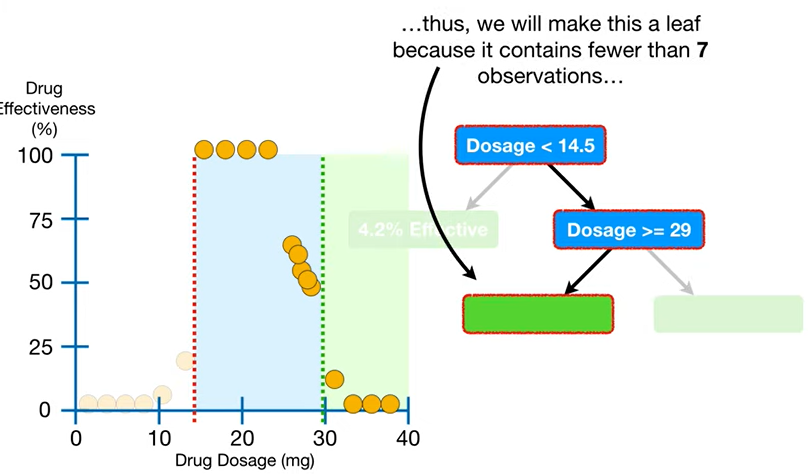
- 오호라, 이제
Dosage>=29인 값도 4개뿐이니까 걔네로 평균 내고 Stop! (과대적합 방지)
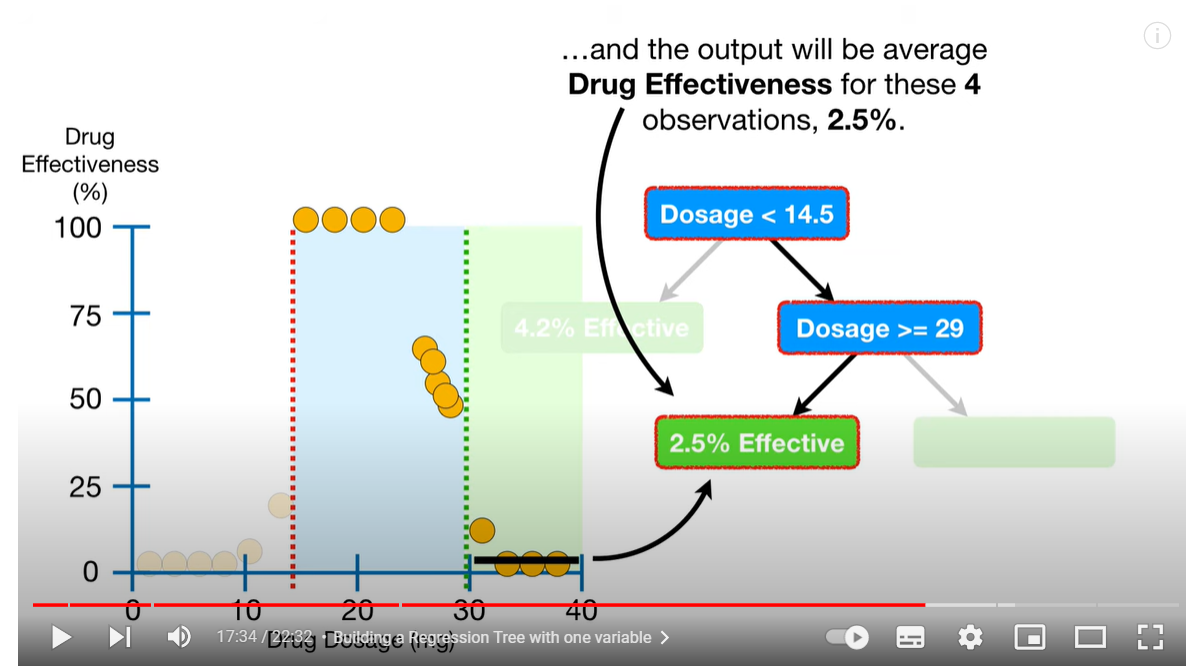
- ☝🏻이제 남은 건,
14.5랑29사이에 잇는 값들이다. 역시 동일한 방식으로 최적의 threshold 찾아서 노드를 분할한다(=트리를 성장시킨다).
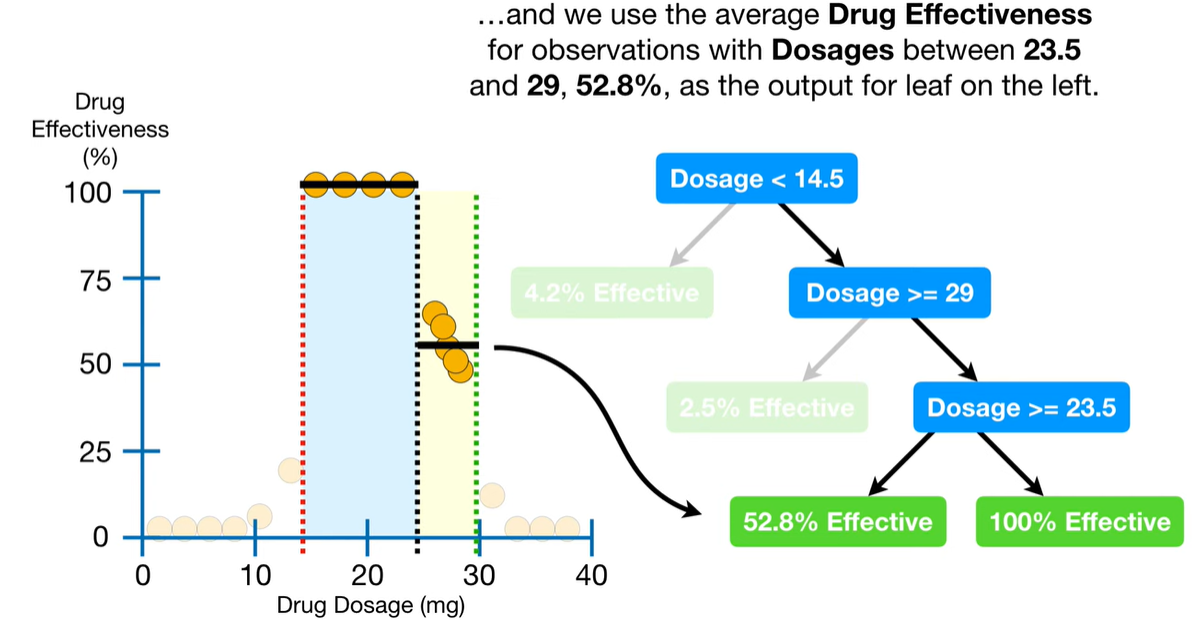
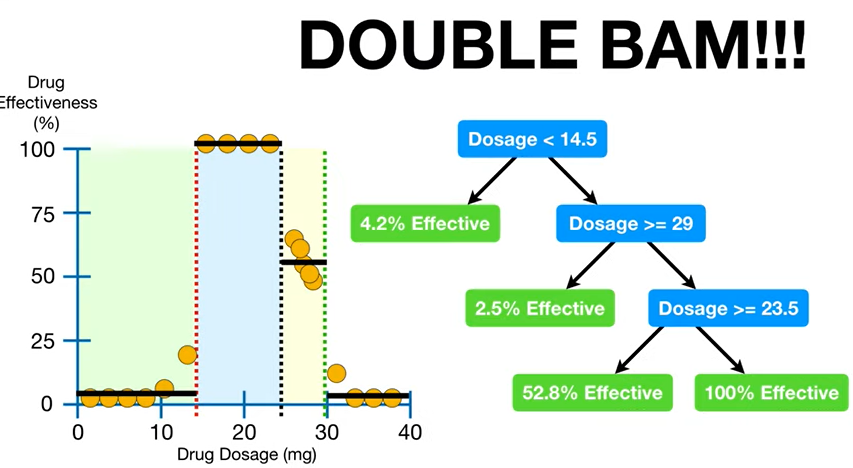
- ☝🏻자 이러면, 더이상 관측값이 7개보다 많이 남은 부분이 없다! = 더 분할 금지!
➡️ '투약량'이라는 독립변수로 '약효'를 예측할 수 있는 결정트리 완성!!! 🙆🏻♂️
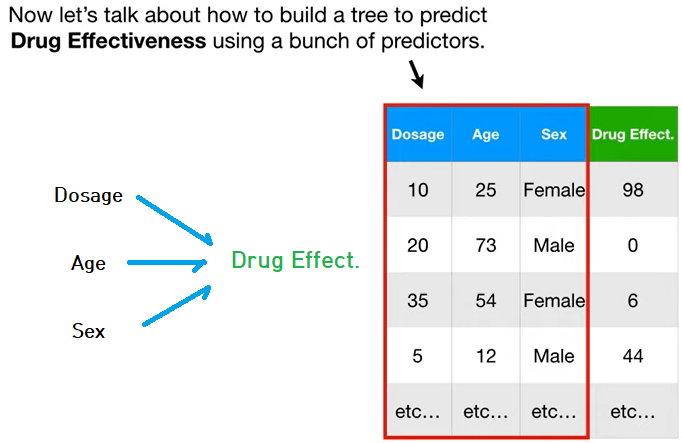
다양한 독립변수 추가
- 지금까지는 '투약량'이라는 하나의 독립변수만 있었다면,
이제는 여러 개의 독립변수들이 추가된 상황을 보자.
- ☝🏻자 그럼 다시, 루트부터 시작한다. → 각 독립변수들마다 최적의 threshold 찾기를 위에서 했던 방법으로 찾는다. → 그 각각의 threshold들이 다 후보가 된다.
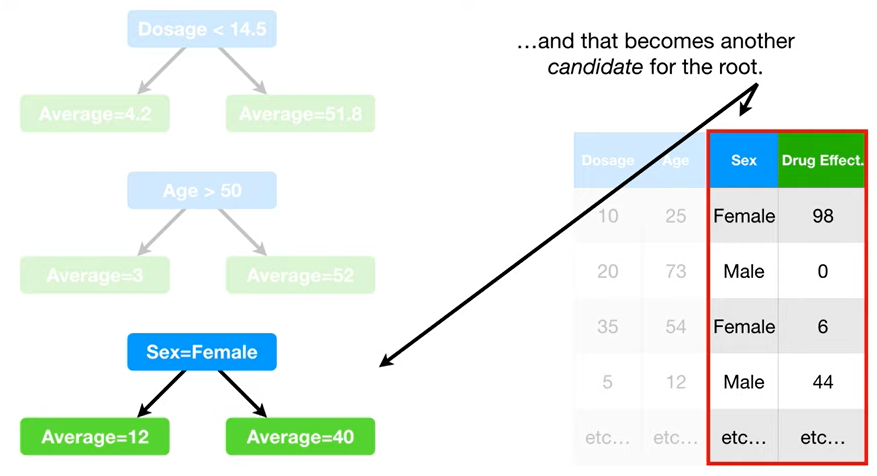
- 그리고 그 후보들끼리 다시 잔차제곱합을 비교해서, 제일 작은 것으로 최종 선정!
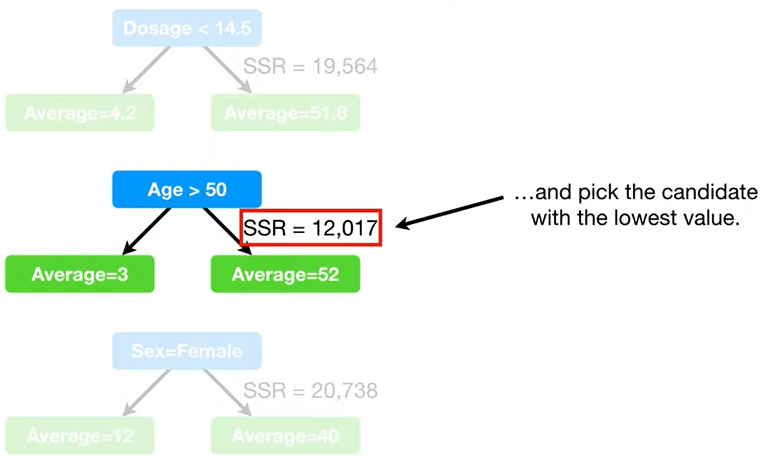
- ☝🏻그리고 이 과정을, 또 반복하면서 쭉 쭉 내려가면 된다!!
+ 노드에 남은 관측값이 7개보다 적어지면 성장을 멈추는 것도 똑같이!!
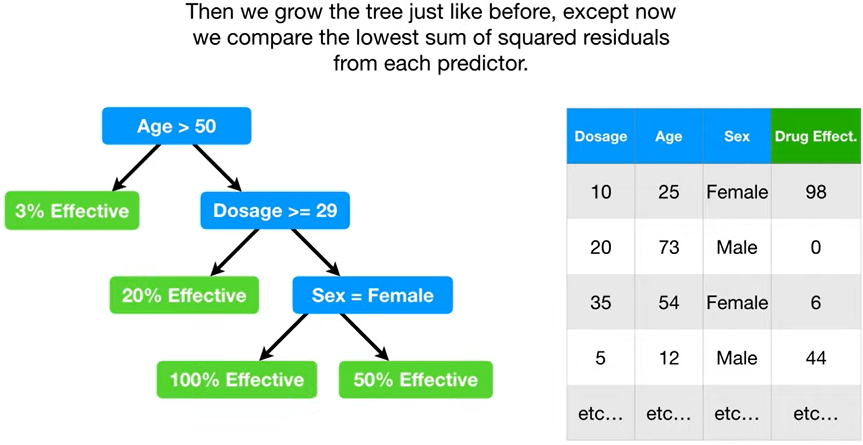
- ➡️이러면 여러 독립변수가 있는 회귀트리도 완성!!! 🙆🏻♂️
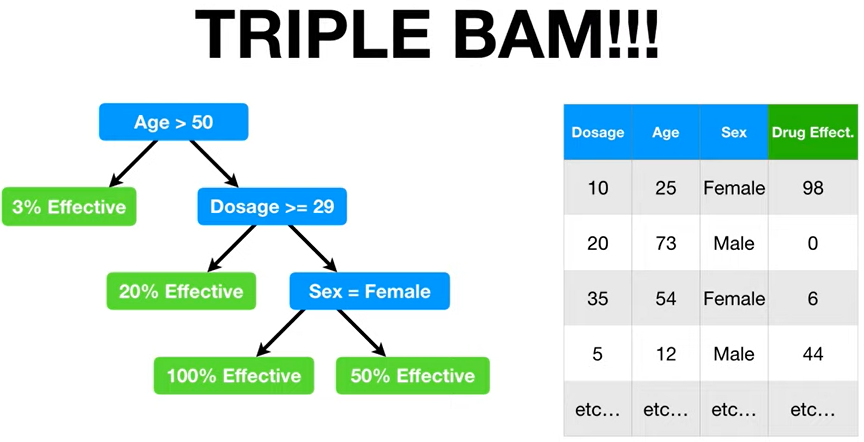
Thank you, Josh Starmer! :)