Intro.
농어 담당 직원이 50cm 짜리 농어를 가져와 무게를 예측해달라고 하시네.
저번 시간에 만든 k-최근접 이웃 회귀 모델을 실전에 쓸 때가 왔군 ㅎㅎ
"1.03kg 정도로 예측됩니다! ... 네...? 실제 무게는 1.5kg이라구요...?" ㅠ zㅠ
1. k-최근접 이웃의 한계
데이터 준비 & 모델 훈련
- 이전 시간에 만든 그 회귀모델 다시 준비 (k=3으로 설정)
문제 상황 파악
- 50cm 농어를 넣어보니 정말 1.03kg로 예측하네 .. (≠1.5kg)
- 산점도로 그려보니 문제가 보임..!
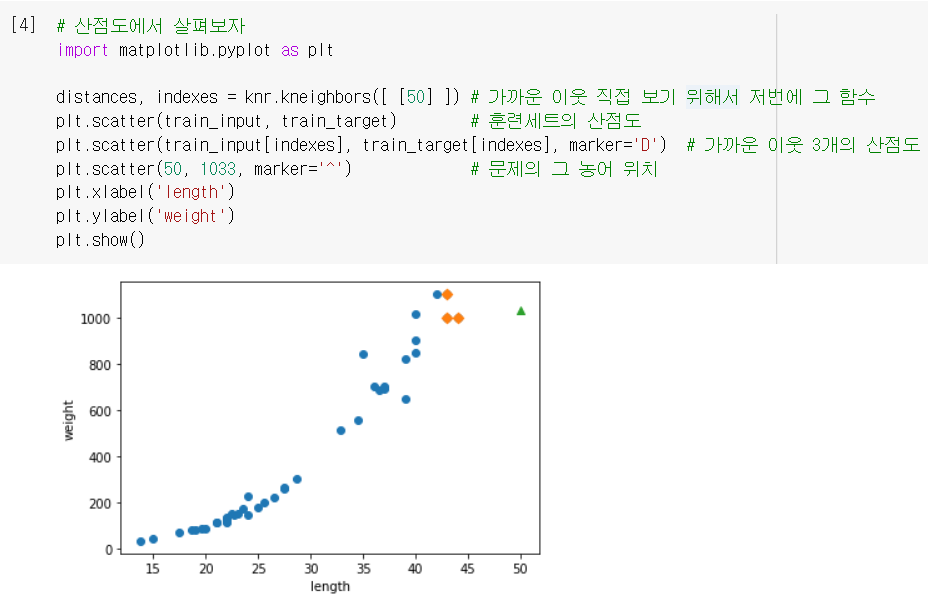
- 새로운 샘플이 훈련세트 범위를 벗어나면 예측을 제대로 할 수 없구나!
(그러니까 아래처럼 100cm를 넣어봐도 그대로 1.03kg으로 예측함 ^^;;)
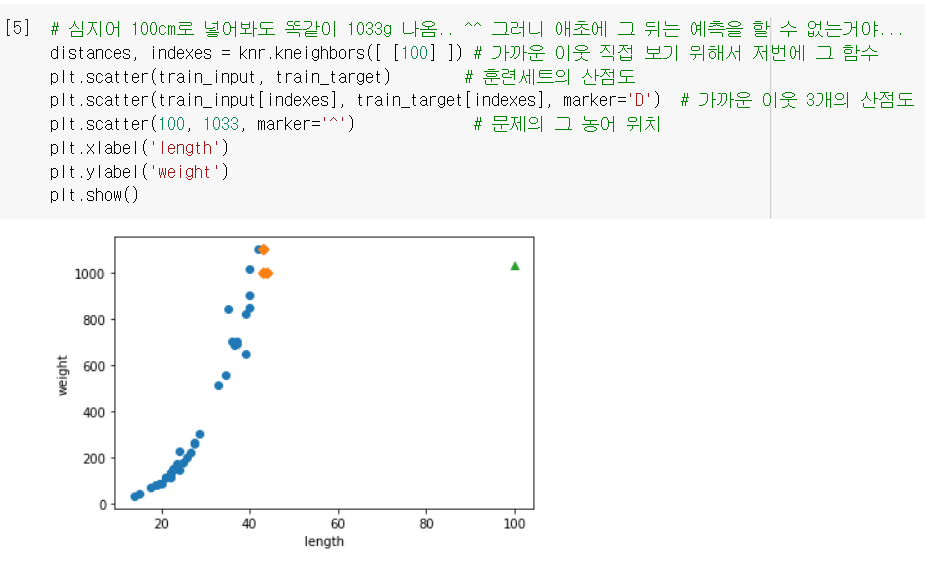"다른 알고리즘을 찾아보자 ...!"
2. 선형 회귀
모델 훈련
- 같은 데이터를 선형회귀 모델(
LinearRegression())로 훈련하고,
다시 50cm 농어 넣어보니 아까보단 나음!
- 선형회귀는 (특성이 하나일 때) 특성을 가장 잘 나타내는 직선을 학습함.
= 적절한.coef_(계수) 와.intercept_(절편) 을 찾아냄!
- 그 계수(가중치)와 절편으로 직선 그려볼 수 있음.
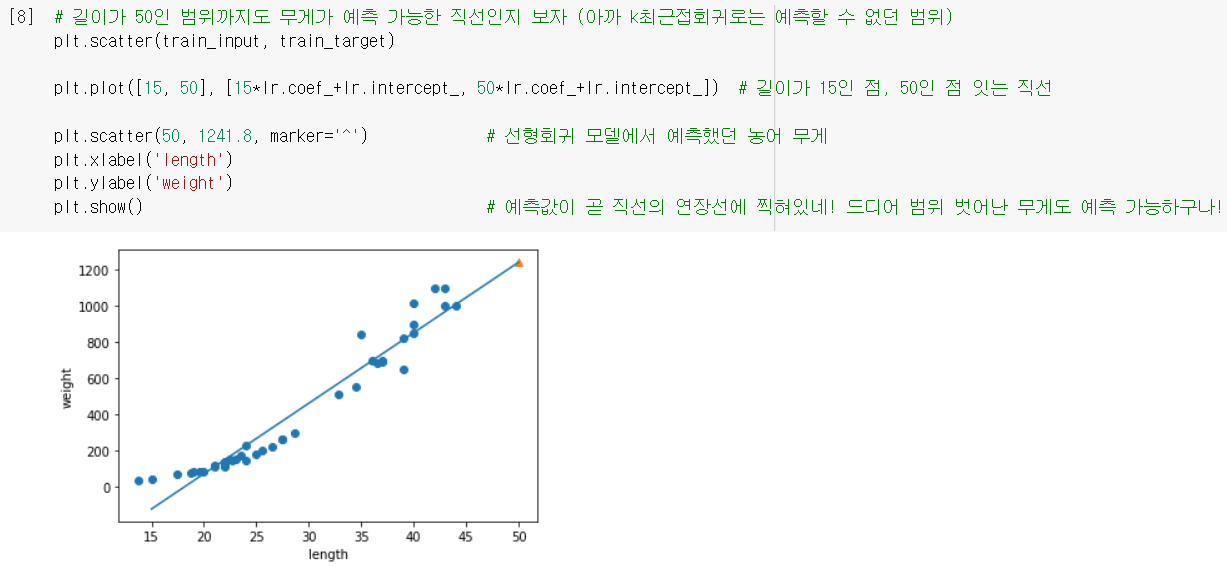
모델 평가
.score로 평가해봤더니, 전체적인 과소적합 문제 발견... ( 둘 다 너무 낮음)
- 게다가, 직선 보면 무게(y값)가 음수인 이상한 구간이 존재함..
"산점도 분포를 보니, 차라리 직선 말고 곡선을 찾는 게 낫겠는데?
그럼 일차식이 아니라 이차식으로 해보면 되겠군..!"
3. 다항 회귀
데이터 준비 (제곱항 추가)
- 길이를 제곱한 column을 만들어서 앞에 붙임 (
.column_stack(())사용)
모델 훈련 & 다시 예측
- 곡선을 학습하는 다항회귀 모델을 쓰니까, 거의 1.5kg에 들어맞게 됐음!
- 마찬가지로 계수, 절편 구해지니까 곡선 그려볼 수 있음.
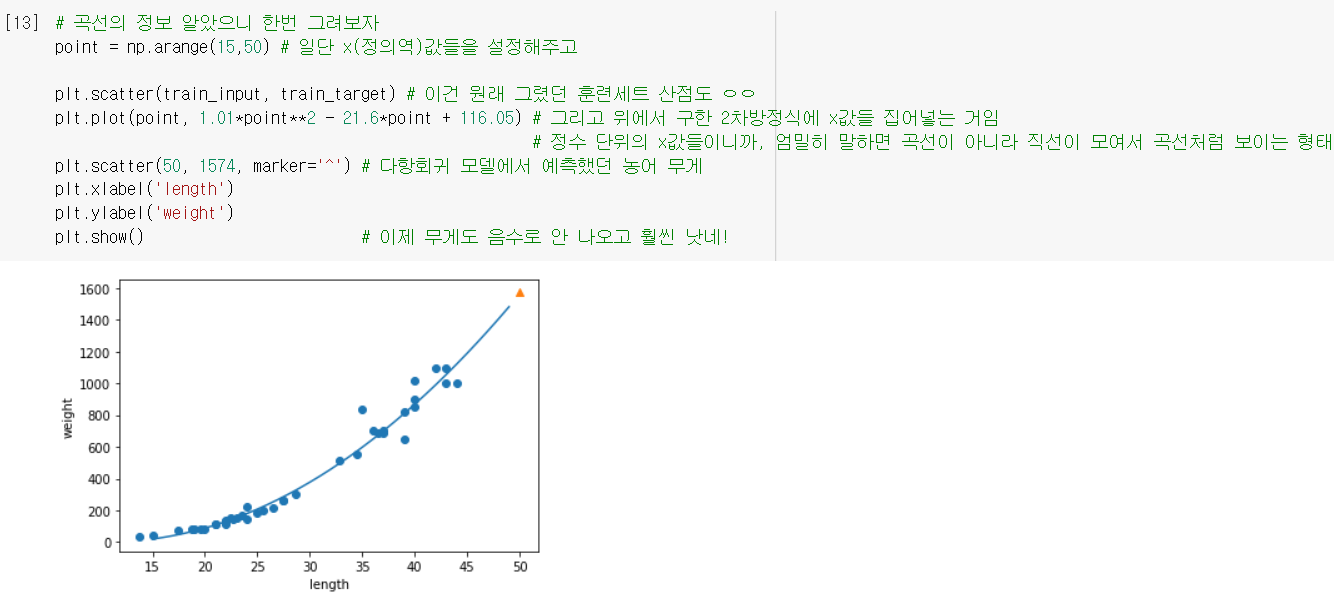
모델 평가
- 그냥 선형회귀로 했을 때 있었던 과소적합이 많이 좋아졌음!
"근데 여전히 과소적합 약간 있는 것 같으니,, 다음 시간엔 더 복잡한 모델 만들어보자!"
➕플러스 알파
➊ 모델 파라미터
- 머신러닝 알고리즘(모델)이 '학습'하여 찾은 값.
- 주로
_를 꼬리표로 붙이고 있음
ex).coef_,.intercept_등
➋ 다항회귀 🆚 다중회귀
- 다항회귀는 동일한 특성을 제곱하는 방식으로 만든 다항식임. → 여기서 고차항은 원래 특성(일차항)에 독립적이지 않음!
ex) - 다중회귀는 아예 특성 종류 자체가 여러 개인 다항식임. → 여기서 각 항들은 서로 독립적임!
ex)
🤔 Hmmmm...
138p.
.score의 값이 높은지의 기준은 무엇인가요..? 142p에서도 아직 과소적합이라고 그러니까 더 혼란스럽군요 ...어느정도가 적당한지는 문제 상황이나 도메인마다 다릅니다. 예측이 힘든 주제는 0.8만 되어도 굉장히 높다고 하고, 예측이 쉬운 문제라면 0.9로도 부족하겠죠. 절대적인 기준은 없습니다..! 🆗
141p. 계수가 다 구해졌다면 그냥 실수범위에서 부드러운 곡선을 그릴 수 있을 텐데요.. 굳이 직선을 이어붙여서 그리는 특별한 이유가 있을까요?
맷플롯립 등의 그래프 라이브러리는 좌표 값을 직접 전달해 주어야 합니다.
정수 대신 더 촘촘한 실수를 넣어도 되지만 시각적으로 큰 차이는 없습니다. 🆗 (좌표값 어차피 일일이 넣어야하는데, 촘촘하게 한다고 큰 차이 없으니 그냥 정수로 했다는 말씀이신 듯!)
🤓 To wrap up...
k-최근접 이웃회귀로 농어 무게 예측하는 데 한계가 있음= 범위 너머의 샘플은 예측 불가
→ 선형회귀 쓰니까 훈련세트 범위 너머도 예측 가능! → but 문제가 몇 가지 있었음 (무게가 음수인 부분 존재, 전반적인 과소적합) → 다항회귀 써서 곡선으로 예측하니까 훨씬 굿!
오늘은 회귀 알고리즘을 드디어 배웠다! (저번 시간의 k-최근접 회귀는 회귀모델이라고 하기도 좀 그러니까..^^) 선형회귀 역시 통계학에서 배워둔 개념이라 이해가 더 수월했던 거 같다. 대신 다항회귀는 처음 봤다! 선형회귀의 확장으로 '중다회귀'는 배웠었는데 그거랑은 결이 다른 개념인 듯하다. (여기서 말하는 '다중회귀'가 그 '중다회귀'일 듯!)
