backtracking 너도 초면이야
반갑지 않지만 반가와^^
Q_15650) N과 M (2)
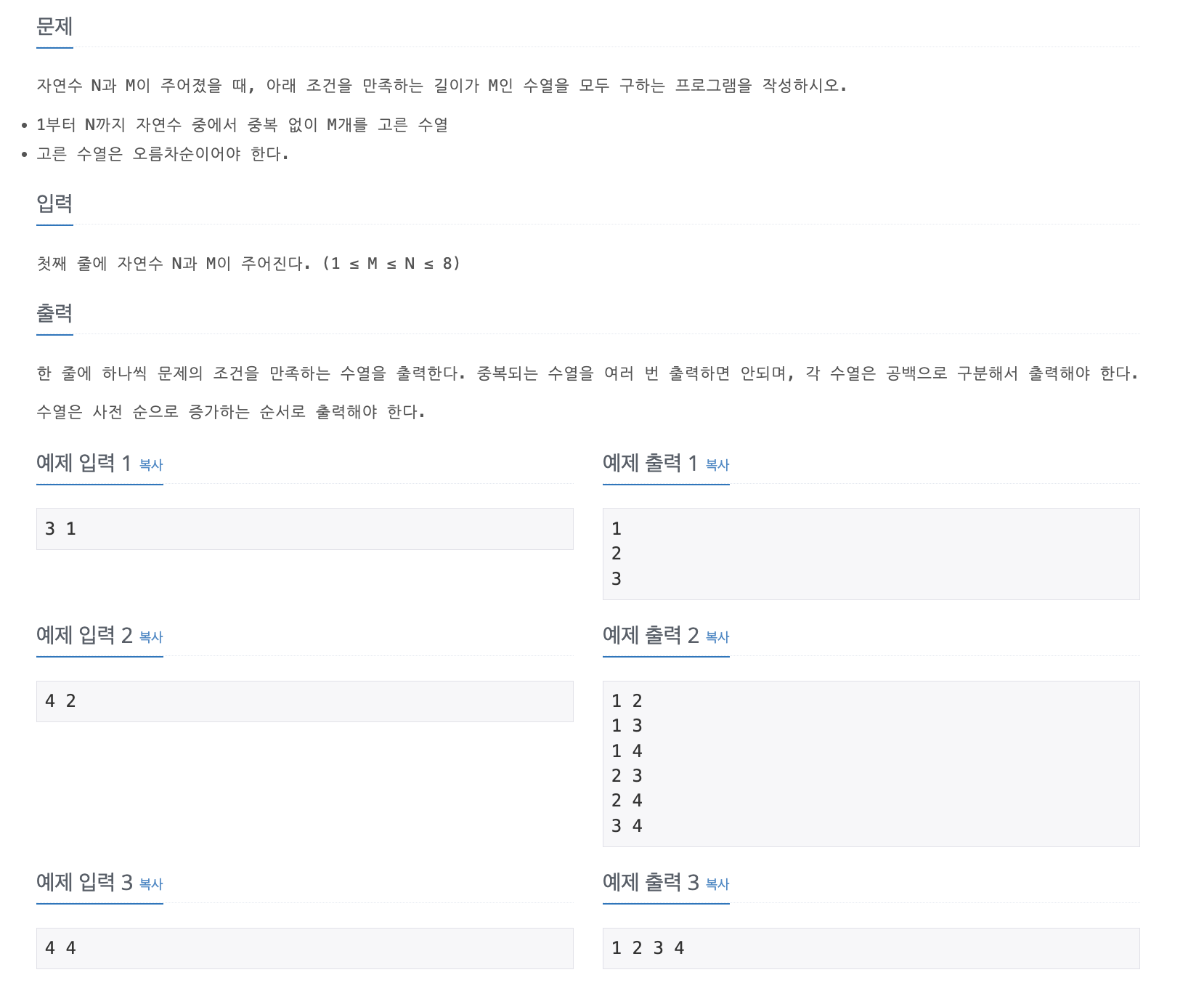
출처 : https://www.acmicpc.net/problem/15650
import java.io.*;
import java.util.*;
public class Prac {
static boolean[] visited;
static int[] num;
static int[] arr;
static int n;
static int m;
static int index = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
arr = new int[n];
visited = new boolean[n];
num = new int[m];
for (int i = 1; i <= n; i++) {
arr[index++] = i;
}
recur(0);
}
public static void recur(int r) {
if (r == m) {
for (int z : num) {
System.out.print(z + " ");
}
System.out.println();
} else {
for (int i = 0; i < n; i++) {
if (!visited[i]) {
for(int j = 0; j < i; j++){
visited[j] = true;
}
visited[i] = true;
num[r] = arr[i];
recur(r + 1);
visited[i] = false;
for(int j = 0; j < i; j++){
visited[j] = false;
}
}
}
}
}
}백트래킹도 초면이라^.^
인프런 강의를 참조했다.
재귀함수를 반드시 써야한다.
풀이:
1) 입력값을 n에 1부터 넣어야하는 마지막 숫자, m에 선택해야 하는 숫자의 개수를 넣는다.
2) arr라는 배열에 n만큼의 길이를 할당해서 1부터 n까지 삽입한다. visited 배열당 인덱스에 있는 숫자가 방문되었는지 확인하기 위해 n만큼의 길이를 할당해서 생성한다. num은 만들어지는 조합을 넣어둘 배열이다.
3) index 0부터 시작해서 recur 메소드를 실행한다.
4) recur 메소드는 recursive이기 때문에 base case와 recursive case로 나눠진다.
4-1) recursive case에서는 인덱스 n을 돌면서 해당 숫자가 visited 안 했다면 visited[i]를 true로 변경하고 그 숫자를 num에 삽입한다.
4-2) recur(r+1)을 실행시키면서 num의 배열을 채워준다.
4-3) 그 후 backtracking 을 위해서 visited[i]를 다시 false로 바꿔준다.
4-4) base case에서는 r이 m과 같다면 num 배열의 요소들을 프린트한다.
여기까지가 인프런에서 등장했던 중복순열을 구하는 방법이다.
나는 중복이 없는 순열을 구해야 했다.🙃
+5) 여기서 j가 등장하는 for loop을 해당 index보다 작은 숫자들을 다 true 처리해주기 위해서다.
ex) num[0]=1일 경우를 다 완료하고 num[0]=2일 경우를 잴 때, 이미 숫자 1일 갔다가 backtracking 했기 때문에 visited[0]은 false로 되어있다. 그래서 for (int i =0..) 부분과 num[r] = arr[i] 부분에서 arr[0], 즉 1을 다시 확인하게 된다.
이 경우를 배제하기 위해서 해당 index보다 작은 index들은 visited 배열에서 true 처리한다.
그리고 마찬가지로 visited[i]를 다시 false로 재설정할 때 똑같이 false로 재설정한다.
*중복순열을 다 구한 뒤, list에 배열 형식으로 중복 순열을 다 삽입해두고 그 배열[0] < 배열[1]을 요소로 갖고 있는 배열을 삭제하는 것도 또 다른 방법이지만 그럼 애초에 무의미한 배열을 구하는 데 시간을 써야했기 때문에 이 선택지는 탈락했다.
😇 최근 프로그래머스 내 기준 난이도 있는 문제들을 풀다보니 효율성의 문제에 맞닥뜨렸다.
그냥 문제만 풀면 되는 줄 알았는데 최적의 알고리즘을 써야한다니.
그 뒤로 코테 문제를 풀면서 내가 생각할 수 있는 그나마 나은 알고리즘을 고르려고 한다. 꽤나 킹받지만 재밌댜!