[코테 풀이] Sum of All Subset XOR Totals

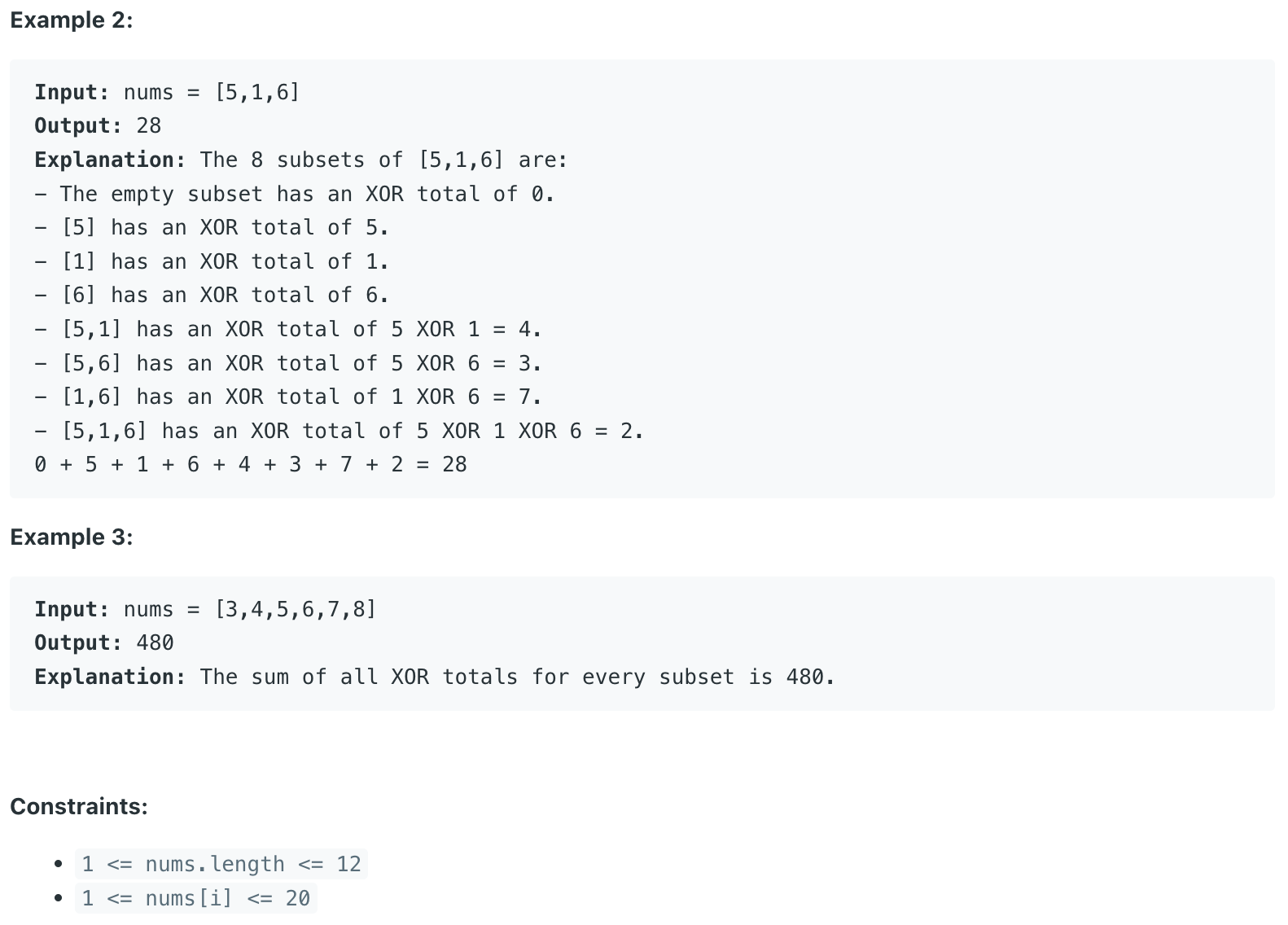
Q_1863) Sum of All Subset XOR Totals

출처 : https://leetcode.com/problems/sum-of-all-subset-xor-totals/submissions/

내 풀이:

class Solution {
   public int subsetXORSum(int[] nums) {
        boolean[] visited = new boolean[nums.length];
        ArrayList<ArrayList<Integer>> total = new ArrayList<>();
        int result = 0;
        for (int l = 0; l <= nums.length; l++) {
            comb(nums, visited, new ArrayList<>(), total, 0, l);
        }
        for (ArrayList<Integer> subset : total) {
            int sum = 0;
            for (int i = 0; i < subset.size(); i++) {
                sum ^= subset.get(i);
            }
            result += sum;
        }

        return result;
    }

    public void comb(int[] nums, boolean[] visited, ArrayList<Integer> arrayList, ArrayList<ArrayList<Integer>> total, int n, int limit) {
        if (arrayList.size() == limit) {
            total.add(new ArrayList<>(arrayList));
            return;
        }
        for (int j = n; j < nums.length; j++) {
            if (!visited[j]) {
                visited[j] = true;
                arrayList.add(nums[j]);
                comb(nums, visited, arrayList, total, j + 1, limit);
                visited[j] = false;
                arrayList.remove(arrayList.size() - 1);
            }
        }

    }
}

🙈 조합 백트래킹 알고리즘 풀이 참조한 문제
오랜만에 기억도 되살릴겸 backtracking으로 subset들을 구하려고 했다
근데 기억이 안 나버려...~
덕분에 이것저것 찾으면서 복기하기

LeetCode 풀이:

class Solution {
    int sum=0;
    public int subsetXORSum(int[] nums) {
        sum=0;
        return getAns(nums,0,0);
    }
    
    int getAns(int[] arr,int i,int cur){
        if(i==arr.length){
            return cur;
        }
        return getAns(arr,i+1,cur^arr[i]) + getAns(arr,i+1,cur);
    }
}

• nums의 숫자들을 포함/미포함하는지에 대한 케이스 분류
• getAns(arr,i+1,cur^arr[i]) 는 포함,
  getAns(arr,i+1,cur) 는 미포함

ex) 만약 nums={1,3} 인 경우,

1) 초기 호출 :

getAns([1, 3], 0, 0)

2) 1 포함하는 경우:

getAns(arr,i+1,cur^arr[i])
=> getAns([1, 3], 1, 1)

• 3 포함하는 경우 : getAns([1, 3], 2, 2) returns 2
  cf) 1^3 = 2
• 3 제외하는 경우 : getAns([1, 3], 2, 1) returns 1

sum: 2 + 1 = 3

3) 1 제외하는 경우:

getAns(arr,i+1,cur)
=> getAns([1, 3], 1, 0)

• 1 포함하는 경우 : getAns([1, 3], 2, 3) returns 3
  cf) 0^3 = 3
• 1 제외하는 경우 : getAns([1, 3], 2, 0) returns 0

sum: 3 + 0 = 3

Final sum: 3 + 3 = 6