문제📝

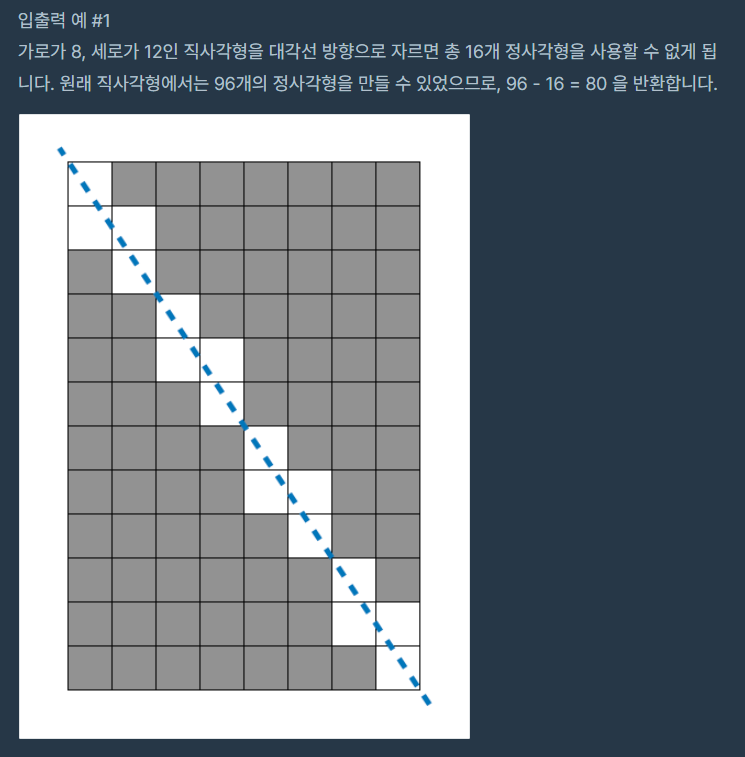
풀이💡
- 최대공약수를 구하는
gcd함수를 만들어준다.- 사용할 수 있는 칸 = (너비*높이) - (너비+높이-최대공약수(너비,높이)이다.
코드💻
/*
* 프로그래머스 Lv2 - 멀쩡한 사각형
* 문제링크:https://programmers.co.kr/learn/courses/30/lessons/62048
*/
class Solution {
public long solution(int w, int h) {
long answer= 0;
long w1 = (long)w; // long형으로 변환
long h1 = (long)h; // long형으로 변환
answer = (w1*h1) - (w1+h1-gcd(w1,h1));
return answer;
}
public static long gcd(long w, long h) { // 최대 공약수
long i=0;
long max = Math.max(w, h); // 최대값 정하기
long min = Math.min(w, h); // 최소값 정하기
for(i=min; i>=0; i--) {
if((w%i==0)&&(h%i ==0)) {
break;
// w%i==0과 h%i==0이 참일 때 가장 먼저 해당되면 최대 공약수
}
}
return i;
}
}결과😎

느낀점👨💻
어떻게 풀어야 할지 감이 안 왔는데 문제를 자세히보니 일종의 똑같은 패턴이 있다는 것을 알게 되어서 그 공식을 구하게 되었고 그 공식을 사용하려면 최대공약수가 필요하다는 것을 알게되어서 별도로 최대공약수 함수를 만들어줘서 문제를 해결할 수 있었다.

