GPT 모델 크기 계산 방법

singleheart·2023년 12월 27일

TL;DR

아래 공식대로 계산하면 쓸만한 근사값이 나옵니다.

모델\,크기 = 12 \times 레이어수 \times 히든노드수 \times 히든노드수

모델 크기는 모델의 파라미터 수를 뜻합니다. 모델이 커질수록 정확합니다.

개요

바야흐르 LLM 시대입니다. 현재의 LLM은 모두 구글의 트랜스포머에서 파생된 GPT 구조로 되어 있는데요.
기사에서 LLM을 소개할 때에 GPT3는 1,750억개의 파라미터다, 메타의 라마2는 70B (700억) 규모이다 등으로 언급하는 것을 볼 수 있습니다.
이런 파라미터 개수는 어떻게 계산할까요? GPT 모델의 크기를 학습 전에 계산하는 방법을 설명하겠습니다.

우선, 학습 후에는 그냥 모델 체크포인트 파일의 크기를 보고 2로 나누어주면 됩니다.
이것은 보통 파라미터 하나를 fp16, bf16 등 2바이트로 학습시켜서 그렇습니다.
fp32로 학습한 경우에는 4로 나누어 주어야 하고, 최신 모델이라서 fp8 학습을 했다면 나누어줄 필요가 없습니다.

계산 방법

학습 후에는 모델의 크기를 쉽게 알 수 있지만, LLM은 한번 학습하는 데 오래 걸리기 때문에 학습 전에 공식을 통해 파라미터 수를 계산하고 싶습니다.
GPT의 구조를 알면 모델 크기를 계산할 수 있습니다.

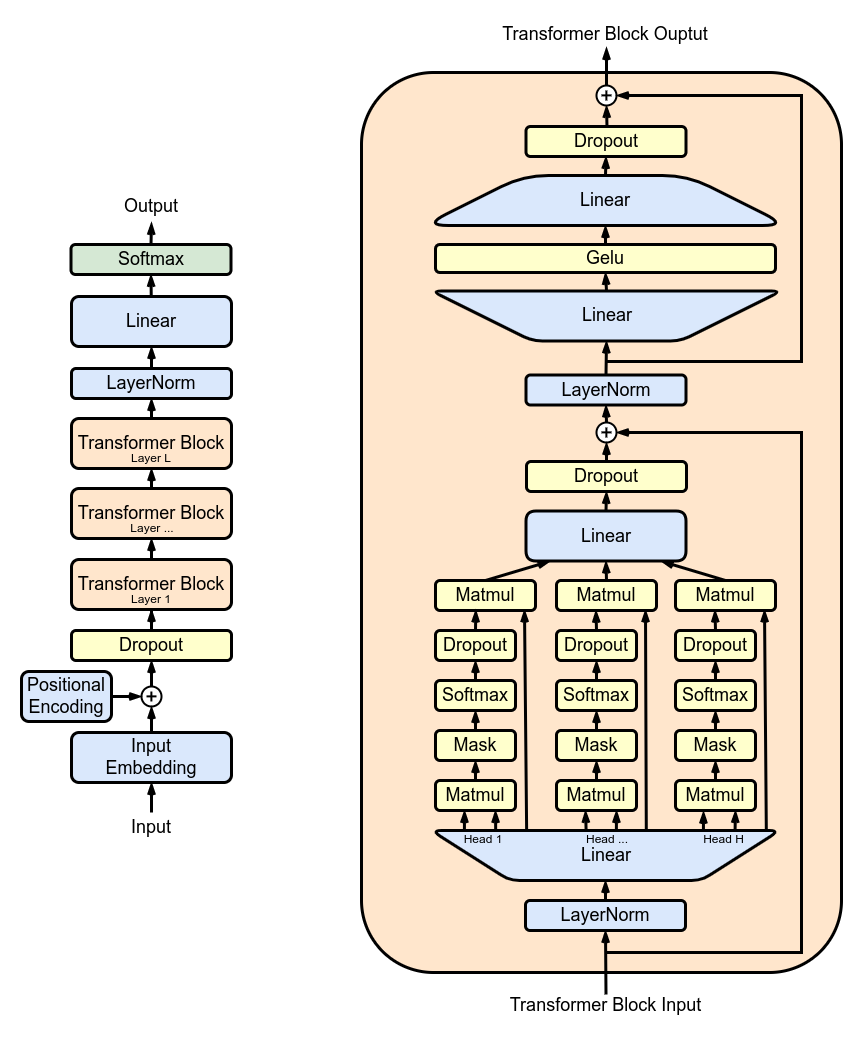
위 그림에서 왼쪽 그림은 GPT의 전체 구조이고요, 오른쪽 그림은 트랜스포머 블록 하나를 자세히 보여줍니다.
블록이 여러 개가 있는데 모두 구조가 똑같기 때문에 파라미터 수를 계산할 때에는 블록 개수를 곱해주면 됩니다.
이제 이 그림에 따라서 파라미터 수를 확인해 보겠습니다.

임베딩 레이어

입력 임베딩

왼쪽 그림에서 Input Embedding에 해당합니다. 입력 토큰을 히든 노드 수에 맞게 임베딩해야 하므로 어휘 수( $vocab\, size$ )와 히든 노드 수( $hidden\,size$ )를 곱합니다.

vocab\, size \times hidden\,size

위치 임베딩

왼쪽 그림에서 Positional Encoding에 해당합니다. 입력의 길이에 맞추어 모든 히든노드에 위치를 더해주어야 하므로 입력 문장 길이( $seq\,length$ )와 히든 노드 수( $hidden\,size$ )를 곱합니다.

seq\,length \times hidden\,size

트랜스포머 블록

모든 블록이 같은 구조 같은 크기입니다. 따라서 한 블록의 크기를 구한 다음 블록 개수 즉 레이어 수(num layers)를 곱해줍니다.
임베딩 레이어와 달리 트랜스포머 블록에 등장하는 레이어들은 weight와 bias가 있습니다.

입력 정규화 레이어

오른쪽 그림을 보면 트랜스포머 블록은 입력에 LayerNorm을 적용하는 것으로 시작합니다. 정규화는 모든 히든 노드에 대해 적용되므로 크기도 히든 노드 개수와 같습니다.

hidden\,size

정규화 레이어는 weight와 bias의 크기가 같습니다.

셀프 어텐션

오른쪽 그림에서 Matmul-Mask-Softmax-Dropout으로 나타나는 단계인데 저장되는 것은 Q, K, V의 weight와 bias입니다.
weight는 각각의 히든노드에 대해 다른 모든 히든노드가 대응하므로 제곱해 줍니다. 여기에 Q, K, V 3가지이므로 3을 곱해줍니다.

3\times hidden\,size \times hidden\,size

bias도 비슷한데 노드당 1개씩이므로

3\times hidden\,size

가 됩니다.

이제 오른쪽 그림을 보면 각각의 QKV 헤드로 나뉘었던 연산들이 행렬곱셈(Matmul) 후에 Linear 레이어를 거칩니다.
이 레이어 역시 히든 노드들을 같은 개수의 히든 노드들로 연결시키기 때문에 weight는

hidden\,size \times hidden\,size

개가 됩니다. bias는

hidden\,size

개가 됩니다.

셀프 어텐션 후 정규화 레이어

입력 정규화 레이어와 같습니다. weight, bias 모두

hidden\,size

개입니다.

멀티 레이어 퍼셉트론 (MLP)

오른쪽 그림에서 Linear - Gelu - Linear로 이어지는 부분입니다.
Linear는 앞의 셀프 어텐션에서도 나왔는데 여기와 모양이 다릅니다. Gelu를 향해 넓어졌다가 다시 좁아지는 모양을 하고 있습니다.
MLP에서 히든 노드 수를 4배로 늘렸다가 다시 원래대로 줄이기 때문입니다.
이를 각각 h to 4h linear layer와 4h to h linear layer라고 부릅니다.
Gelu 활성화 함수는 파라미터를 따로 갖지는 않습니다.

h to 4h linear layer

weight는 $4 \times hidden\,size \times hidden\,size$
bias는 $4 \times hidden\,size$ 입니다.

4h to h linear layer

h to 4h linear layer와 같습니다. 같은데 왜 굳이 따로 설명하고 있을까요?
Gelu가 아니라 SwiGLU 등 다른 활성화 함수를 쓰는 경우에는 파라미터 수가 달라질 수 있기 때문입니다. 이 포스팅에서는 생략합니다.

마지막 정규화 레이어

앞에서 등장한 정규화 레이어들과 똑같이 $hidden\,size$ 파라미터입니다. 순서가 헷갈릴 수 있기 때문에 똑같아도 다시 언급합니다.
정규화 레이어는 weight와 bias의 크기가 같습니다.

모두 합치면

크게 보아 아래와 같이 계산할 수 있습니다

모델 크기 (파라미터 수) = 임베딩 + 블록\,수 \times 블록당\,파라미터\,수 \times 마지막\,정규화레이어\,크기

임베딩과 마지막 정규화 레이어를 대입해 보면

모델 크기 = vocab\,size \times hidden\,size + seq\,length \times hidden\,size + num\,layers \times 블록당\,파라미터 수 + 2\times hidden\,size

블록당 파라미터 수는

입력 정규화 + 셀프어텐션_{QKV} + 셀프어텐션_{linear} + 셀프어텐션\, 후\, 정규화 + MLP

이므로

2\times hidden\,size + 3\times hidden\,size\times hidden\,size + 3\times hidden\,size + hidden\,size\times hidden\,size + hidden\,size + 2\times hidden\,size + 2\times (4\times hidden\,size\times hidden\,size + 4\times hidden\,size)

인데 정리하면

4\times hidden\,size + 12\times(hidden\,size \times(hidden\,size + 1))

이 됩니다. 이제 모두 대입하면

모델 크기 = vocab\,size\times hidden\,size + seq\,length \times hidden\,size + num\,layers \times (4\times hidden\,size + 12\times (hidden\,size \times(hidden\,size + 1))) + 2\times hidden\,size

이제 $vocab\,size$ , $seq\,length$ , $hidden\,size$ , $num\,layers$ 를 알면 모델 크기를 정확히 구할 수 있습니다.

근사값 구하기

앞의 네 가지 정보는 모델을 학습하든 갖다쓰든 구하기 쉬운 정보입니다. 따라서 정확히 계산하는 데에 문제는 없습니다.
우리한테는 계산기도 있고요. 다만 공식이 길어서 외우기 힘듭니다. 다행히 공식을 잘 보면 간단히 근사값을 구할 수 있습니다.
알고리즘의 시간복잡도 개념을 떠올려 보면 공식에 $x^2$ 등 큰 항목이 있으면 $x$ 같은 작은 항목은 대세에 영향을 주지 않습니다.
이 공식에서도 $hidden\,size$ 를 제곱하는 것이 눈에 띕니다. 제곱이 포함된 가운데만 남기면 어떨까요?

모델 크기 = num\,layers \times 12 \times(4 \times hidden\,size + hidden\,size\times(hidden\,size + 1))

여기서 $4\times hidden\,size$ 나 $+ 1$ 등은 대세에 큰 영향이 없음을 알 수 있습니다. 이것들을 제외하면

모델 크기 = num\,layers\times 12\times hidden\,size \times hidden\,size

여기서 12를 맨 왼쪽으로 옮기면

모델 크기 = 12 \times num\,layers \times hidden\,size \times hidden\,size

간단한 공식이 나타났습니다. $num\,layers$ 와 $hidden\,size$ 만 알면 계산할 수 있습니다.

이 근사값은 얼마나 정확할까요? NVIDIA의 Megatron-LM에서 사용하는 모델 크기로 확인해 보겠습니다

모델명	파라미터 수	근사값
125M	165,299,712	84,934,656
345M	409,339,904	301,989,888
1.3B	1,422,659,584	1,207,959,552
6.5B	6,872,375,296	6,442,450,944
39B	39,516,651,520	38,654,705,664
175B	174,619,385,856	173,946,175,488

모델이 커질수록 실제 파라미터 수와 근사값이 점점 비슷해집니다. 제대로 된 근사 공식이라고 봐도 되겠습니다.

※ 데보션 블로그에도 올렸습니다.

singleheart

개발자

이전 포스트

HuggingFace로 16비트 모델을 저장하고 불러오기

다음 포스트