함수포인터
일반적인 함수포인터
//type (*name)(param...)
void (*fp)();
void func()
{
cout << "AAA" << endl;
}
int main()
{
fp = func;
fp();
return 0;
}멤버 함수 포인터
class Test
{
public:
void func()
{
cout << "AAA" << endl;
}
};
//type (class::*name)(param...)
void (Test::*fp)();
int main()
{
Test t;
fp = &Test::func;
(t.*fp)();
return 0;
}운영체제
기본용어
프로그램
어떤 작업을 실행할 수 있는 파일
Job = 프로그램 + Data
프로세스
컴퓨터에서 연속적으로 실행되고 있는 프로그램
적어도 1개 이상의 쓰레드를 보유
쓰레드
실질적으로 연산을 수행하는 단위
각각이 stack을 보유
프로세스의 code, data, heap은 공유
알고리즘
시간복잡도, 공간복잡도 고려가 필수적임.
일반적으로 시간복잡도를 더 중요하게 여김.
Big O 표기법
데이터 개수에 따라 소요되는 시간을 표현한 것.
정렬
참고 : https://gyoogle.dev/blog/algorithm/Bubble%20Sort.html
거품정렬
인접한 두 원소를 비교하여 자리를 교환.
가장 끝에서부터 정렬.
시간복잡도 : O(n2)
공간복잡도 : O(n)
swap이 많이 발생.
선택정렬
원소를 넣을 위치가 결정되어 있고, 넣을 원소를 결정하는 알고리즘.
시간복잡도 : O(n2)
공간복잡도 : O(n)
삽입정렬
정렬을 진행하면서 일부가 정렬되어있음 = 정렬된 리스트에 새 데이터를 넣을 장소를 찾는 알고리즘
Think : 삽입 정렬과 이진 탐색을 함께 쓰는 것도 좋을 듯.
원소를 결정한 후, 넣을 위치를 결정하는 알고리즘.
쉘 정렬의 일부로 사용.
어느정도 정렬된 배열에 대해서 속도가 빠름.
시간복잡도 : O(n2)
공간복잡도 : O(n)
쉘정렬
참고 : https://gmlwjd9405.github.io/2018/05/08/algorithm-shell-sort.html
삽입 정렬이 어느정도 정렬된 배열에 대해 속도가 빠르다는 것에서 착안한 알고리즘.
일정한 간격 단위로 삽입 정렬을 수행.
(최악)시간복잡도 : O(n2)
(평균)시간복잡도 : O(n1.5)
공간복잡도 : O(n)
참고 : 거품정렬부터 쉘정렬까지 O(n2)로 동일하지만, swap의 수가 적어서 조금씩 더 빠르다.
퀵정렬
pivot을 결정한 후, pivot을 기준으로 정렬.
분리된 부분끼리 반복.
만약 중간에 위치할 값을 미리 안다면 최적으로 수행할 수 있을 것임
ex) 0~100까지의 값의 범위라면 50을 찾아서 pivot으로 삼는다.
다만, 이런 경우라도 값이 한 곳에 몰려있다면(1, 2, 3, 4, 50, 100) 최적이라고 장담할 수 없음
(최악)시간복잡도 : O(n2)
(평균)시간복잡도 : O(nlog2n)
공간복잡도 : O(n)
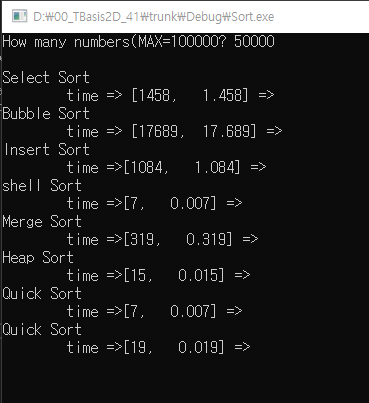
참고 : 교재에 나온 직접 구현한 qsort가 MSVC의 qsort보다 빠른것을 볼 수 있는데, 이는 MSVC에서 사용하는 비교 함수의 호출 비용으로 인해 발생.
참고 : 마찬가지로 qsort를 재귀함수로 구현할 경우, 재귀호출의 비용도 나름 비싸다고 볼 수 있음.
다이어그램
시퀀스 다이어그램과 클래스 다이어그램은 필수.
정리하는 느낌으로 작업 중 틈틈히 작성.
시퀀스 다이어그램
https://www.websequencediagrams.com/
처음 보는 코드를 시퀀스 다이어그램을 이용하면 쉽게 분석할 수 있음.
클래스 다이어그램
MSVC에서도 참조 구조가 가능.