10.21

Camera

화면을 채우는 카메라 조정

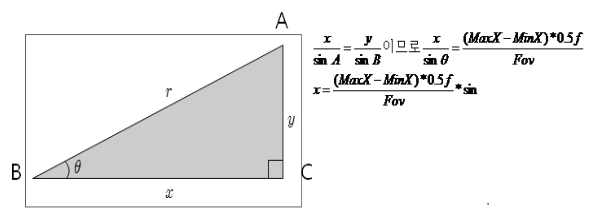
Camera의 FOV와 Target Object가 주어졌을 때 Object를 화면에 가득 채우기 위한 Camera의 Distance 조정
삼각형 비례 : $Distance = \frac{radius}{tan(fov * 0.5)}$
사인공식 :

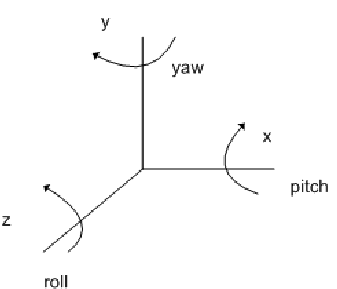
오일러 각

강체가 놓인 방향을 3차원 공간에 표시하기 위해 사용한 3개의 각도

오일러 각을 이용해 회전시킬 경우 ZXY순으로 회전을 많이 시키는데, 이는 가장 사용 가능성이 적은 각을 먼저 곱해서 짐벌락 현상을 최소화 하기 위한 것으로 보인다.

짐벌락

행벡터를 오일러각으로 회전시키는 공식

최종행렬을 보면 2열이 모두 $\theta_x$에 영향을 받는다는 것을 확인할 수 있음.
다시말해 $\theta_x$가 $90^\circ$, $270^\circ$이 되면 2열은 (0, 0, -1)이 되므로 z축은 회전 성분이 모두 사라지는 것을 볼 수 있음
이처럼 1번째 회전 성분이 2번째 회전 성분의 특정 회전각에 따라 자유도가 상실되는 현상을 짐벌락이라고 함

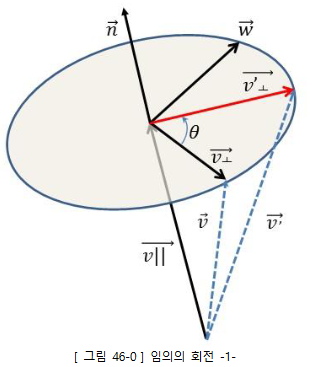
임의의 축에 대한 회전

이 때 임의의 축이란 Local 좌표계의 원점을 중심으로 한 임의의 축을 의미

$v^\prime = (1 - cos\theta)(\vec{n} \cdot \vec{v})\vec{n} + cos\theta \vec{v} + sin\theta(\vec{n} \times \vec{v})$

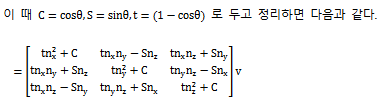
내적 $(\vec{n} \cdot \vec{v})$를 분해해서 $\vec{v}$에 대한 행렬로 나타낼 수 있다는 점에 주의

임의의 점에 대한 회전

모든 회전은 원점에 대하여 돌아간다. 다시말해 임의의 점에서 회전을 하고싶다면 임의의 점을 원점으로 변경하면 된다.
$M_{out} = M_S * (M_{RC})^{-1} * M_R * M_{RC} * M_T$

사원수(Quaternion)

실수 1개와 허수 3개를 사용해 표현하는 방법. 허수부는 기저 벡터, 실수부는 회전각을 의미

Reference : 사원수와 2차원 회전 - https://chessire.tistory.com/entry/%EC%82%AC%EC%9B%90%EC%88%98%EC%BF%BC%ED%84%B0%EB%8B%88%EC%98%A8-Quaternion%EC%97%90-%EB%8C%80%ED%95%98%EC%97%AC

Reference : 사원수와 3차원 회전 - https://jebae.github.io/quaternion-rotation

사원수를 이용한 정점의 회전

$v^\prime = qVq^*$
$q^*$는 켤례 사원수

사원수의 장점

짐벌락이 없음
주어진 두 벡터에 대한 회전축(허수부-외적)과 회전각(실수부-내적)이 바로 산출됨
보간을 쉽게 처리할 수 있음
Matrix에 비해 연산량과 저장 장소가 적음

단, Shader의 연산은 Vector 연산만 지원하므로 Matrix로 변환하여 Shader에 넘겨야함

$v^\prime = qVq^*$