소수(Prime Number)

자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수
= 1과 자기 자신 외에 약수가 존재하지 않는 수

1. 소수 검사 방법

1) 딱 하나를 검사할 때

import math

def is_Prime(n):
	for i in range(2, int(math.sqrt(n))+1):
    	if n%i==0:
        	return False
	return True

Q: 왜 범위에 루트를 씌웠는가?
A: 우리는 약수가 있는지 없는지를 판단하는게 메인이다. 그리고 약수라는 것은 쌍으로 존재하는데 그 쌍의 반만 검사해도 충분하기 때문이다.

2) 소수의 집합을 구할때 (에라토스테네스의 체)

1) 구하고자 하는 소수의 범위만큼 1차원 리스트를 생성
2) 2부터 시작하여 자신을 제외한 배수들을 지워나간다

핵심은 이미 지운거의 배수들은 지우지 않고 continue 한다는 것!!
이것을 통해 시간 복잡도를 O(N^2)에서 O(Nlog(logN))까지 줄일 수 있음

import math
n = int(input())
num = [True]*(n+1)
num[0] = False
num[1]= = False

for i in range(2, int(math.sqrt(n))+1):
	if num[i] == False:
    	continue
    for j in range(i*2, n+1, i):
    	num[j] = False

해당 코드는 num의 인덱스가 소수가 되고, 값은 True:소수/False:소수X가 됨.
계속 배수들을 지워서 소수가 아닌것들을 쳐내어 유용하게 쓸 수 있는 자료형(에라토스테네스의 체)를 만든다.

2. 소수 응용 문제(제곱수)

1) 각 소수당 제곱수 검사시 중복발생 X

소수의 제곱을 검사할 때 서로 겹치는 것은 없다.
검사1: 2, 4, 8, 16, 32 ...
검사2: 3, 9, 27

2) 제곱수의 key = a< x< b에서 a,b를 줄이는 것

제곱수 연산을 해나가게 되면 값이 너무 커진다.
오버플로우 가능성도 존재...
양변을 줄여나가는 것이 key가 됨...
a/x < x < b/x 만족?
a/x/x < x < b/x/x 만족?
...

정수론

1. 오일러 피(서로소 개수)

오일러 피 함수 P[N]의 정의는 1부터 N까지 범위에서 N과 서로소인 자연수의 개수를 뜻한다. -> "N과의 최대공약수가 1뿐임"

# GCD(n,k) = 1
import math
import sys
input = sys.stdin.readline

n = int(input())
result=n

for i in range(2, int(math.sqrt(n)+1)):
    if n %i==0:
        result -= result/i
        while n%i==0:
            n/=i
if n > 1:
    result = result - (result/n)
print(int(result))

1. i로 나누어서 이 값을 빼준다.
   -> 공통된 약수의 개수를 줄인다.
2. N을 i와 공통된 약수가 없개 충분히 줄여준다.(while n%i==0)
   -> N이 줄어들어서 for문 조건에서 가변적임
3. for문 종료시 N이 1보다 크다면 마지막 소인수가 남았다는 뜻
   한번더 연산해준다

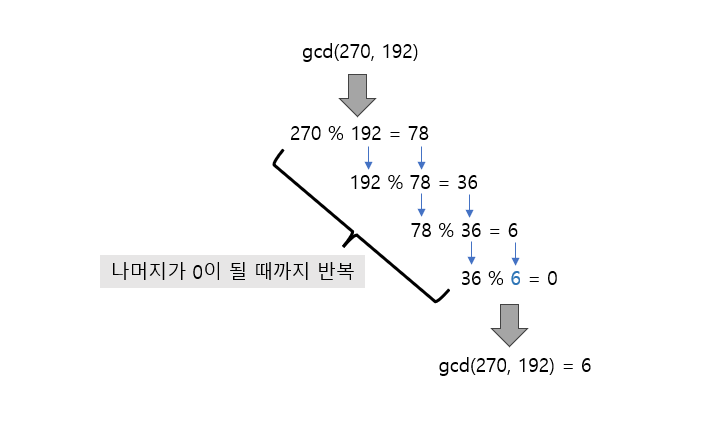
2. 유클리드 호제법(최대공약수, 최소공배수 간단하게 풀 수 있음)

두 수의 최대 공약수를 구하는 알고리즘
소인수 분해 보다 더 간단함

• 주요 Point는 mod 연산을 이용한다는 것....
  

def gcd(a, b):
    if b==0:
        return a
    else:
        return gcd(b, a%b)

• a랑 b의 순서는 상관없음
  why? 3 % 4해도 다시 재귀로 들어갈때 (4 % 3)으로 알아서 바뀜

• 그렇다면 최소공배수는 어떻게?
  두수의 곱을 최대공약수로 나누어 주면 됨
  따라서 유클리드 호제법으로 최소공배수까지 쉽게 구할 수 있음

3. 확장 유클리드 호제법

유클리드 호제법 -> 두 수의 최대공약수
확장 유클리드 호제법 -> 방정식의 해 구하기

ax + by = c(a, b, c, x, y는 정수)

• 위 방정식은 c % gcd(a,b) = 0인 경우에만 정수해를 가짐
  = c가 a와 b의 최대공약수의 배수인 경우에만 정수해를 가짐

ex> 5x+9y=2를 만족하는 x와 y 구하기

• 먼저 확인해야할것 = 2가 gcd(5,9)의 배수인지
  -> 배수가 맞다! 따라서 5x + 9y = 최대공약수 를 가지고 확장 유클리드 진행 가능
  -> 여기서는 최대공약수가 1이다.

유클리드 호제법 실행	나머지	몫
5%9=5	5	0
9%5=4	4	1
5%4=1	1	1
4%1=0	0	4

나머지	몫	x = y', y=x'-y'*q 역순 계산
5	0	X=2, Y=-1-(2*0)=-1
4	1	X=-1, Y=1-(-1*1)=2
1	1	X=1, Y=0-(1*1)=-1
0	4	X=0, Y=1-(0*4)=1

• 처음 시작하는 x와 y는 x'(이전 x)와 y'(이전 y)가 없으므로 1과 0으로 잡고 역순 계산한다.

최종 답은 X=2, Y=-1 이것을 식(5x+9y=1)에 대입해보자!
맞아 떨어진다.
이제 이 최대공약수의 배수인 2에 맞아 떨어져야 하므로 답에 2씩 곱한다
따라서 정답은 X=4, Y=-2이다.