다익스트라 알고리즘?
다익스트라(dijkstra) 알고리즘은 그래프에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘 중 하나이다. 이 과정에서 도착 정점 뿐만 아니라 모든 다른 정점까지 최단 경로로 방문하며 각 정점까지의 최단 경로를 모두 찾게 된다. 매번 최단 경로의 정점을 선택해 탐색을 반복하는 것이다.
과정
① 출발 노드와 도착 노드를 설정한다.
② '최단 거리 테이블'을 초기화한다.
③ 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다.
④ 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트한다.
⑤ ③~④의 과정을 반복한다.
'최단 거리 테이블'은 1차원 배열로, N개 노드까지 오는 데 필요한 최단 거리를 기록한다. N개(1부터 시작하는 노드 번호와 일치시키려면 N + 1개) 크기의 배열을 선언하고 큰 값을 넣어 초기화시킨다.
'노드 방문 여부 체크 배열'은 방문한 노드인지 아닌지 기록하기 위한 배열로, 크기는 '최단 거리 테이블'과 같다. 기본적으로는 False로 초기화하여 방문하지 않았음을 명시한다.
예시
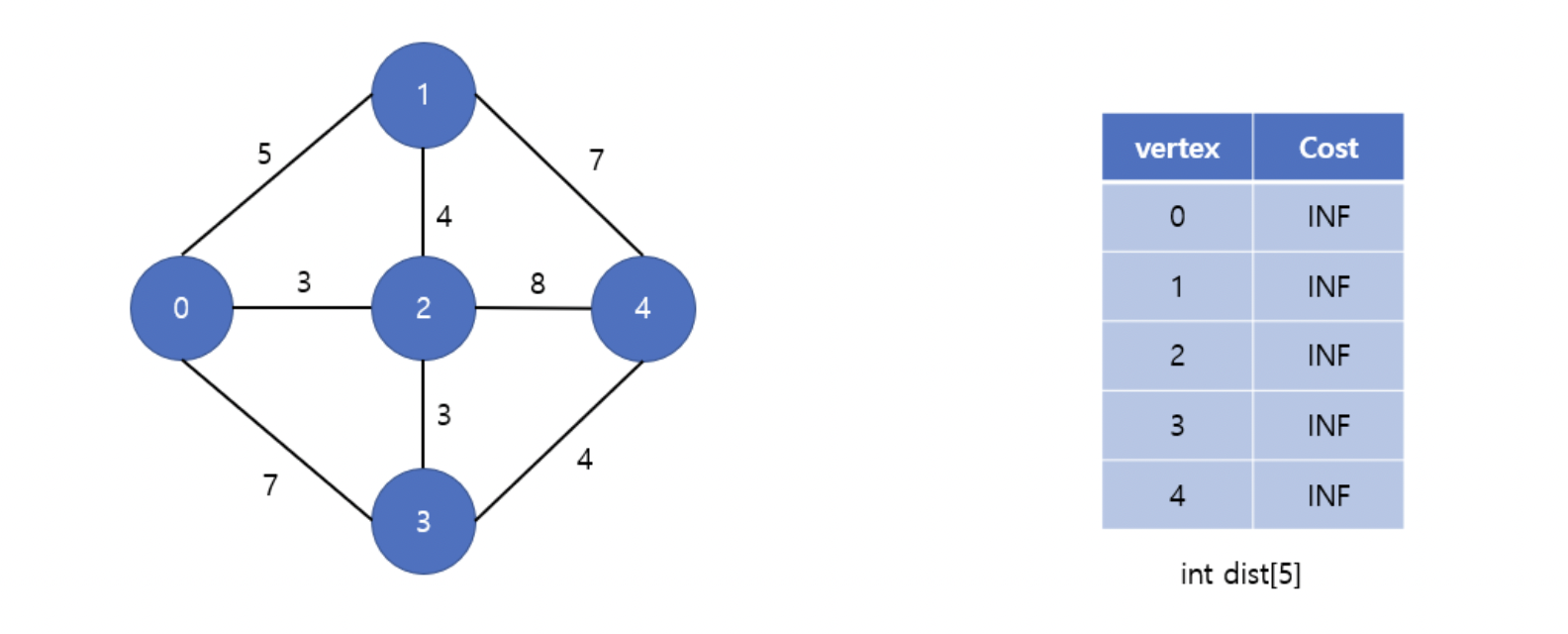
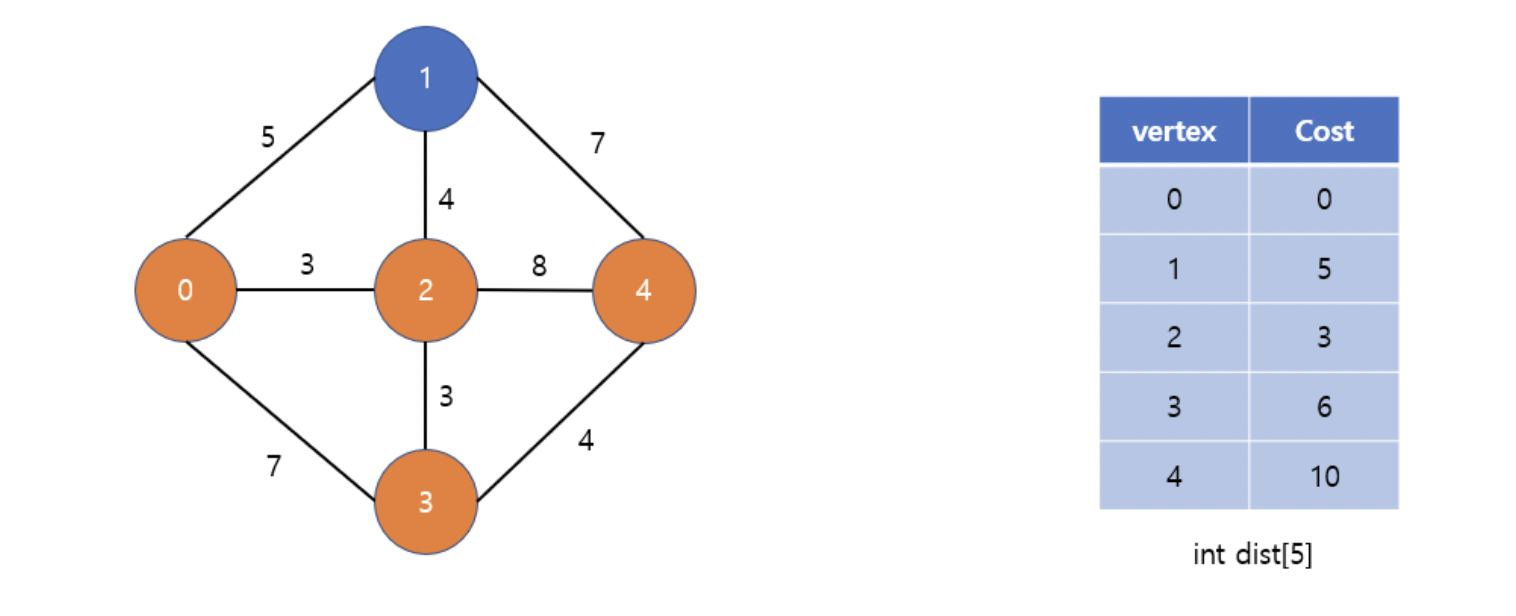
위와 같은 그래프가 있다고 하자. 시작정점은 0번 정점이라고 가정하고 나머지 정점까지의 최단거리를 계산해보자.
1차원 배열 dist[]에 각 정점까지의 최단거리를 갱신해 나갈 것이다. 초기에는 모두 INF(무한대)로 설정한다.
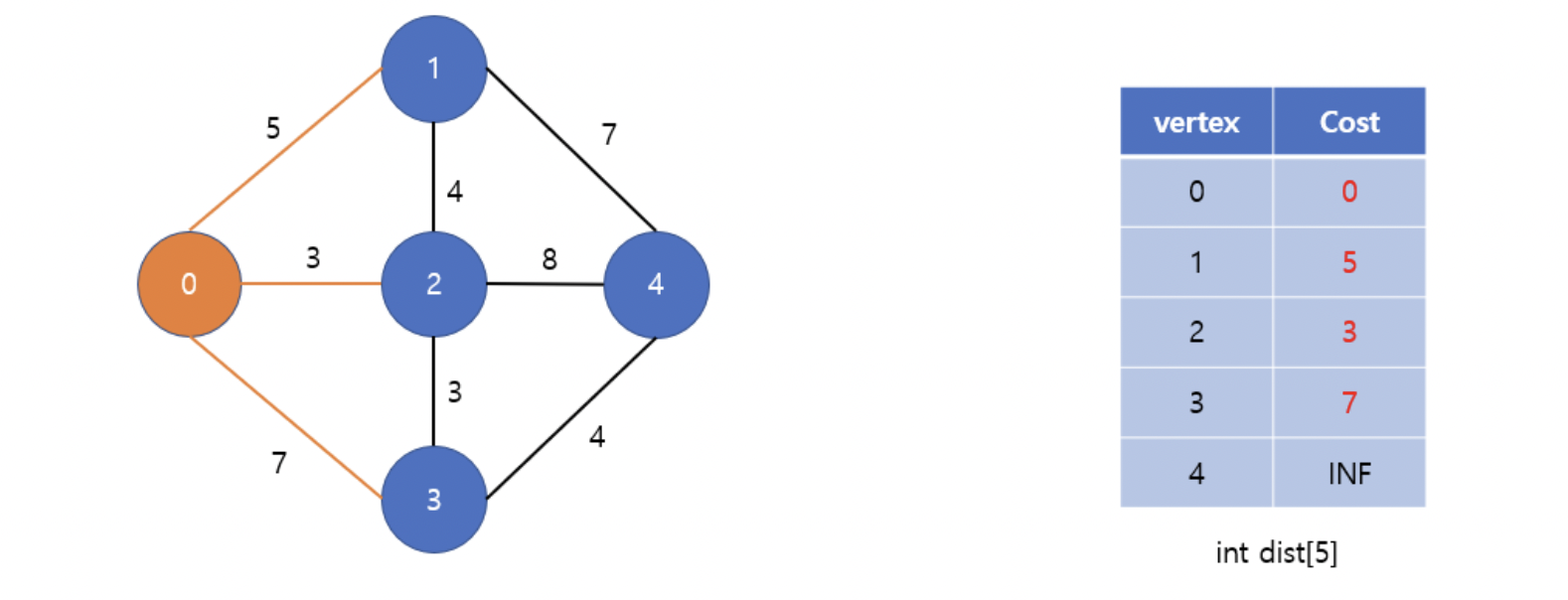
• 가장 먼저 시작정점을 방문한다.
• 시작 정점에서 방문 할 수 있는 정점들에 대한 거리를 갱신한다.
• 방문하지 않은 정점 중 가장 가중치가 작은 2번 정점을 방문한다.
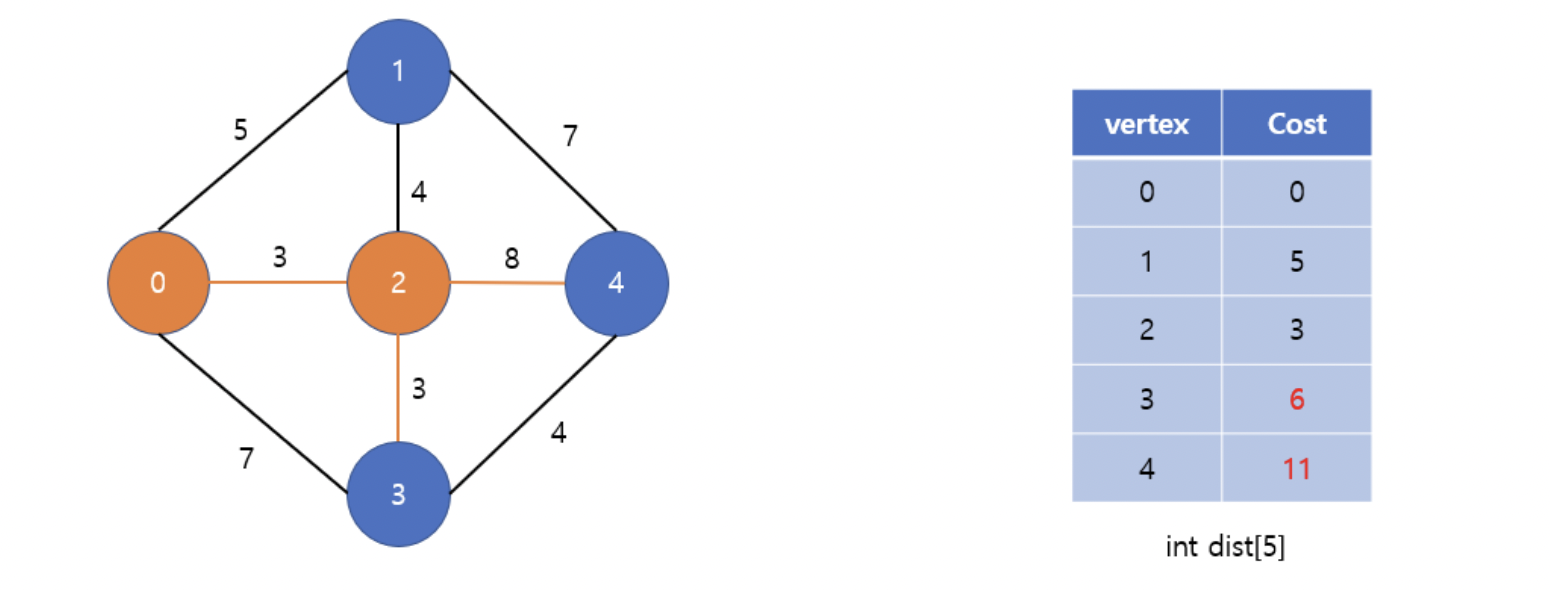
• 0번 정점에서 2번 정점을 거쳐서 4번 정점을 가면 기존 거리 보다 최단 거리이므로 갱신한다. ( INF > 11)
• 0번 정점에서 2번 정점을 거쳐서 3번 정점을 가면 기존 거리 보다 최단 거리이므로 갱신한다. ( 7 > 6 )
• 방문하지 않은 정점 중 가장 가중치가 작은 3번 정점을 방문한다.
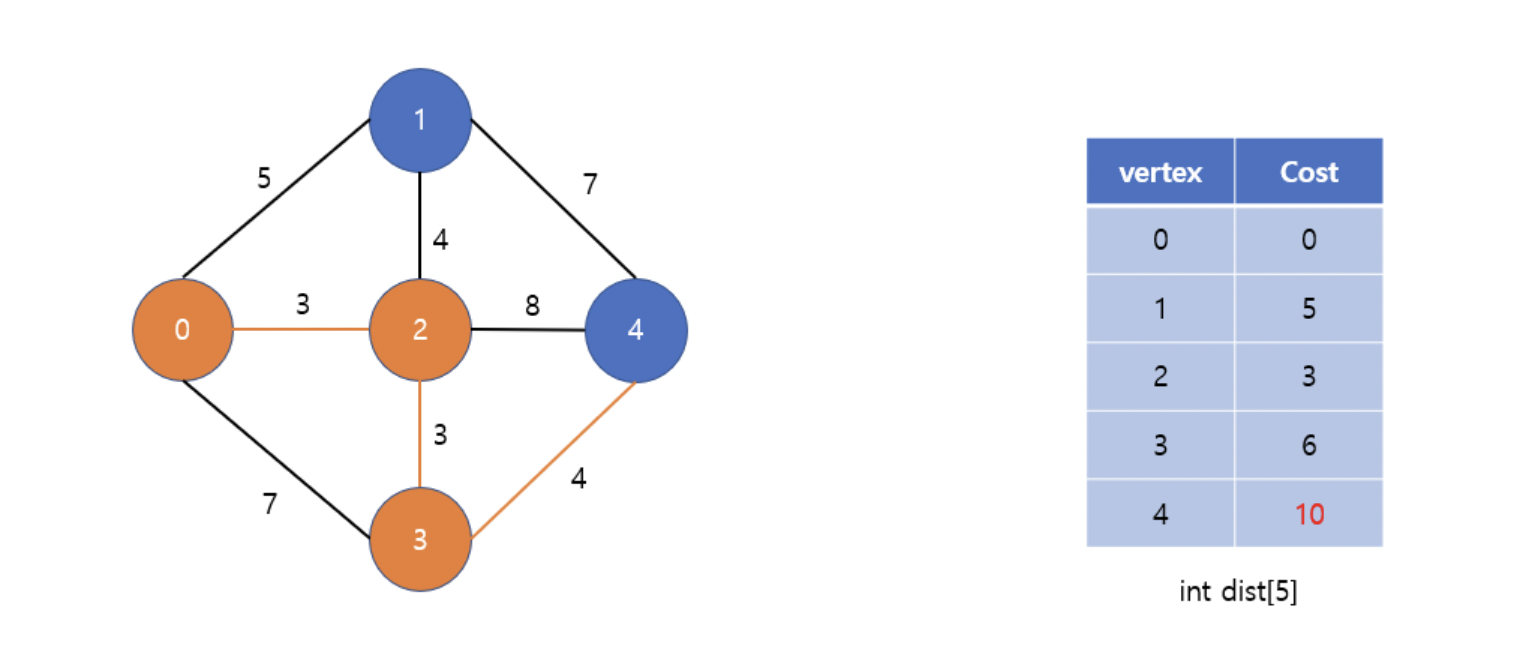
• 0번 정점-2번 정점-3번정점을 거쳐서 4번 정점을 가면 기존 거리보다 최단 거리이므로 갱신한다. ( 11> 10 )
• 방문하지 않은 정점 중 가장 가중치가 작은 4번 정점을 방문한다.
• 갱신할 거리가 없다.
• 방문하지 않은 정점 중 가장 가중치가 작은 1번 정점을 방문한다.
• 갱신할 거리가 없다.
• 모든 정점을 방문했으므로 종료한다.
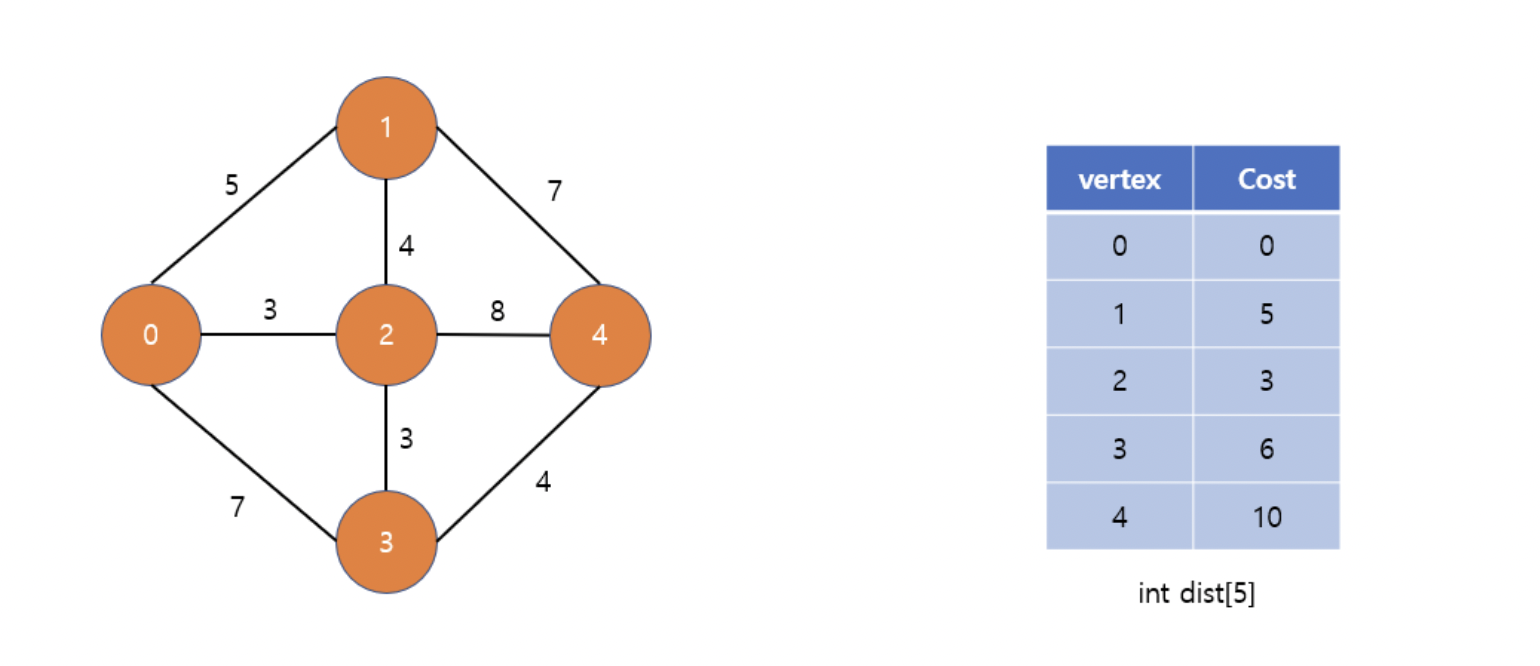
⭐️ 위와 같은 과정을 거치면 dist 배열에 0번정점부터 각 정점까지의 최단거리가 기록되게 된다.
💻 C++ 구현
1. 순차탐색
#include <vector> #include <queue> // 아직 방문하지 않은 노드 중 // 가장 거리값이 작은 노드의 인덱스 반환 int FindSmallestNode() { int min_dist = INF; int min_idx = -1; for (int i = 0; i<= N; i++) { if (visited[i] == true) continue; if (dist[i] < min_dist) { min_dist = dist[i]; min_idx = i; } } return min_idx; } // 다익스트라 void Dijkstra() { for (int i = 1; i <= N; i++) dist[i] = map[start][i]; // 시작 노드와 인접한 정점에 대해 거리 계산 dist[start] = 0; visited[start] = true; for (int i = 0; i < N - 1; i++) { int new_node = FindSmallestNode(); visited[new_node] = true; for(int j = 0; j <= N; j++) { if (visited[j] == true) continue; if (dist[j] > dist[new_node] + map[new_node][j]) dist[j] = dist[new_node] + map[new_node][j]; } } }
2. 우선순위 큐
#include <vector> #include <queue> #include <iostream> using namespace std; # define INF 99999999 // 시작 위치와 정점의 개수, 인접 행렬을 받아 // 최소 거리 행렬을 반환함 vector<int> dijkstra(int start, int N, vector<pair<int, int>> graph[]) { vector<int> dist(N, INF); // 거리를 저장할 리스트 초기화 priority_queue<pair<int, int>> pq; // 우선순위 큐 선언 dist[start] = 0; // 시작 노드 거리를 0으로 함 pq.push({ 0, start }); // 우선순위 큐에 넣기 while (!pq.empty()) { int cur_dist = -pq.top().first; // 큐에서 꺼내 방문하고 있는 정점의 거리 int cur_node = pq.top().second; // 정점의 인덱스(번호) pq.pop(); for (int i = 0; i < graph[cur_node].size(); i++) { int nxt_node = graph[cur_node][i].first; // 인접 정점 번호 int nxt_dist = cur_dist + graph[cur_node][i].second; // 인접 정점까지 거리 if (nxt_dist < dist[nxt_node]) // 지금 계산한 것이 기존 거리값보다 작다면 { dist[nxt_node] = nxt_dist; // 거리값 업데이트 pq.push({ -nxt_dist, nxt_node }); // 우선순위 큐에 넣기 } } } return dist; // start 노드로부터 각 노드까지 최단거리를 담은 벡터 리턴 } int main() { const int N = 10; // 노드의 개수가 10개라 가정. int E = 20; // 간선의 개수가 20개라 가정. vector<pair<int, int>> graph[N]; // 그래프 형태 선언 for (int i = 0; i < E; i++) { int from, to, cost; // 간선의 시작점, 끝점, 가중치 cin >> from >> to >> cost; graph[from].push_back({ to, cost }); // 무향 그래프라 가정하므로 시작점과 끝점 둘 다 벡터에 넣어야 함 graph[to].push_back({ from, cost }); } vector<int> dist = dijkstra(0, N, graph); cout << "끝점까지의 최단거리" << dist[N - 1] << endl; return 0; }
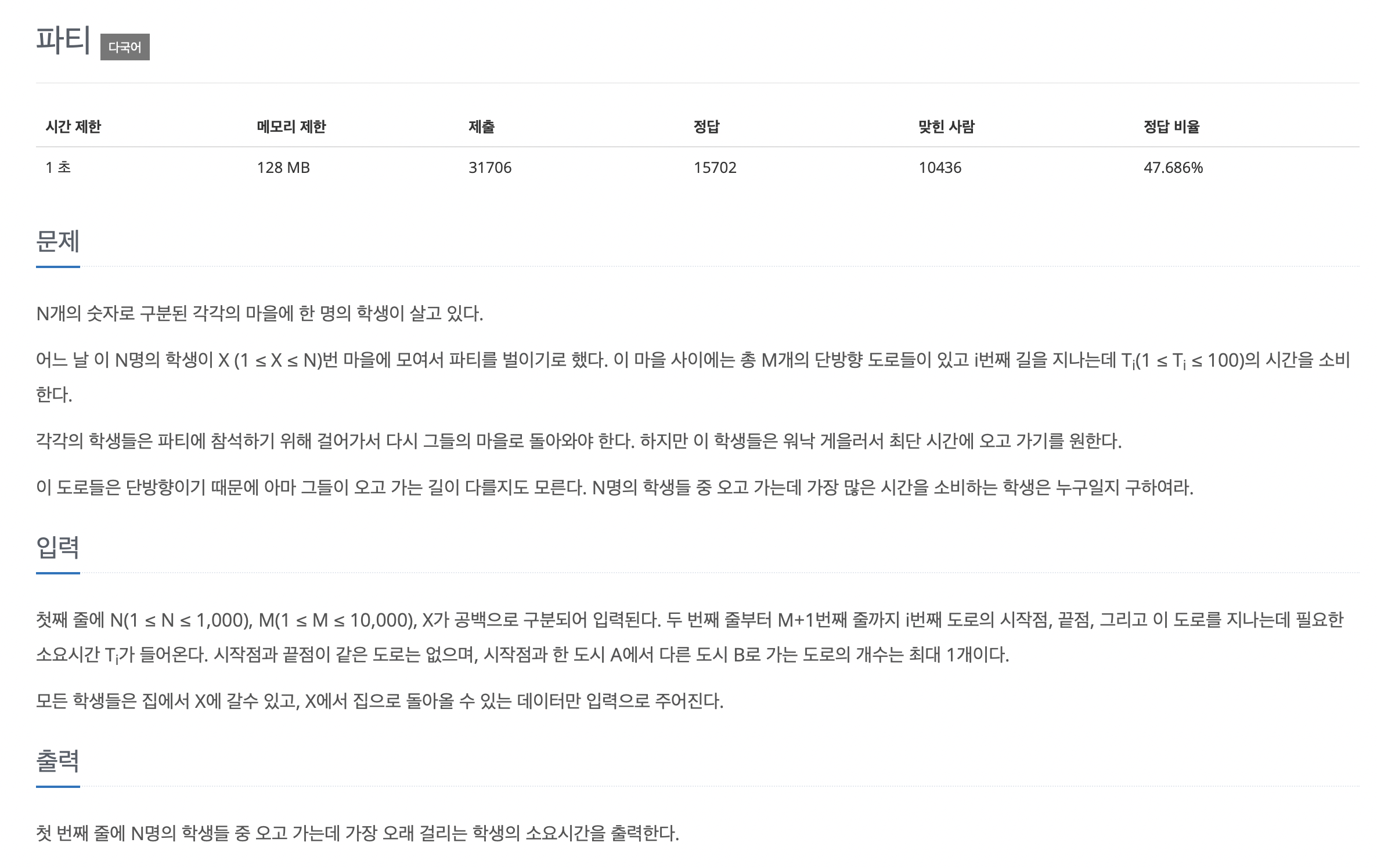
✏️ 백준 1238
#include <bits/stdc++.h> using namespace std; const int INF = 1e9 + 7; int dist_x_to_n[1001]; vector<int> dist[2]; vector<pair<int, int>> graph[2][1001]; int n, m, x; void dijkstra(int k) { dist[k][x] = 0; priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; q.push({0,x}); while (!q.empty()) { int d = q.top().first; int now = q.top().second; q.pop(); if (d > dist[k][now]) continue; for (int i = 0; i < graph[k][now].size(); i++) { int next = graph[k][now][i].second; int next_d = d + graph[k][now][i].first; if (next_d < dist[k][next]) { dist[k][next] = next_d; q.push({ next_d,next }); } } } } int main() { ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); fill_n(dist_x_to_n, 1001, INF); cin >> n >> m >> x; for (int i = 0; i < m; i++) { int a, b, t; cin >> a >> b >> t; graph[0][a].push_back({t,b}); graph[1][b].push_back({ t,a }); } dist[0].resize(n + 1, INF); dist[1].resize(n + 1, INF); dijkstra(0); dijkstra(1); int result = 0; for (int i = 1; i <= n; i++) { result = max(result, dist[0][i] + dist[1][i]); } cout << result << '\n'; return 0; }
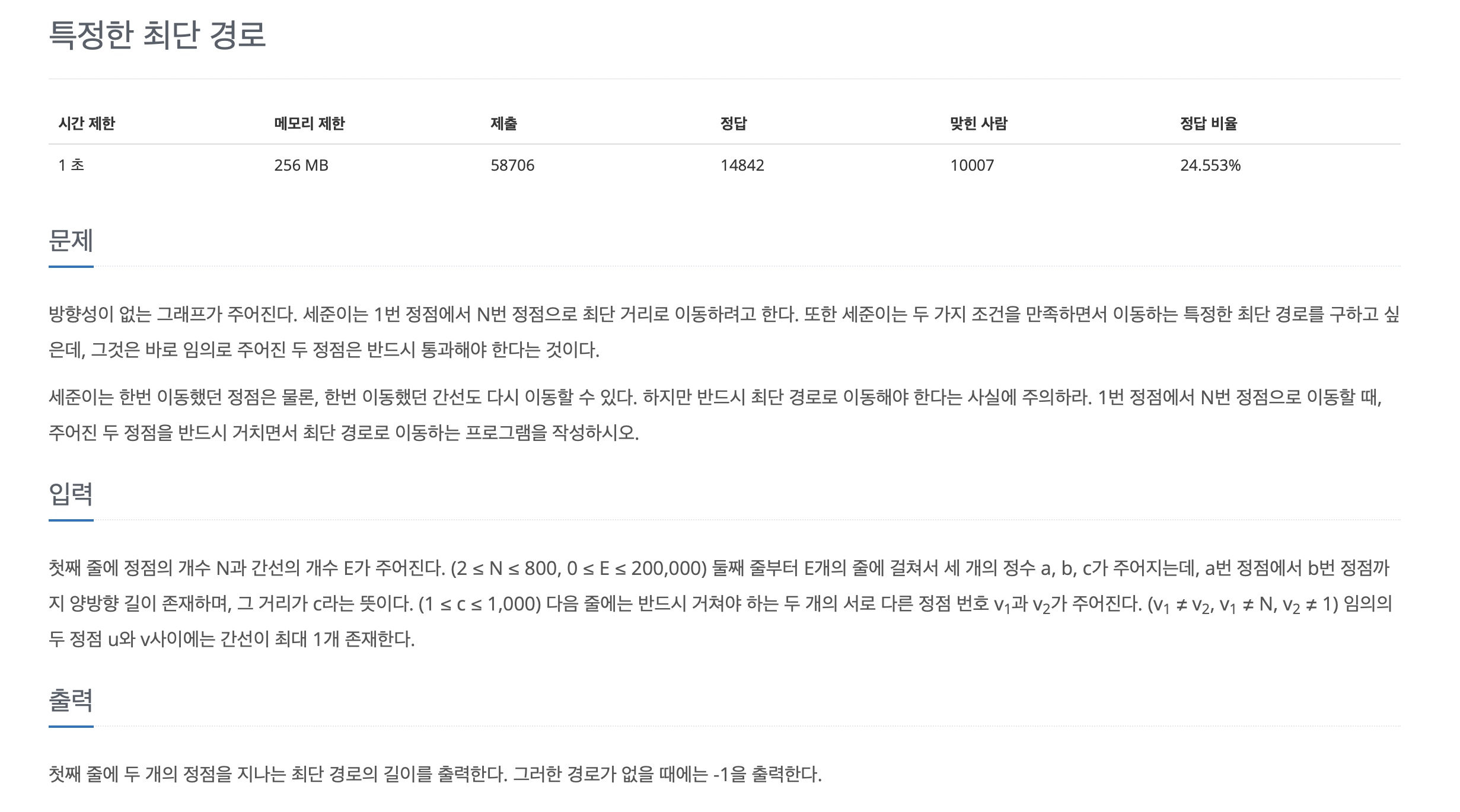
✏️ 백준 1504
#include <iostream> #include <vector> #include <queue> #include <algorithm> #include <cstring> using namespace std; const int INF = 987654321; int N, E, v1, v2, res = INF; int sToV1, sToV2, V1ToV2, V1ToN, V2ToN; vector<pair<int, int>> v[801]; // v[a] = (b,c) : a에서 b까지 c의 거리로 이동 가능 int dist[801]; void dijk(int start) { for (int i = 0; i <= N; i++) dist[i] = INF; dist[start] = 0; priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; q.push({ 0,start }); // 현재까지 거리, 현재 위치 while (!q.empty()) { int cur = q.top().second; int curDist = q.top().first; q.pop(); for (int i = 0; i < v[cur].size(); i++) { int next = v[cur][i].first; int nextDist = v[cur][i].second; if (dist[next] > curDist + nextDist) { dist[next] = curDist + nextDist; q.push({ dist[next],next }); } } } } int main() { cin >> N >> E; while (E--) { int a, b, c; cin >> a >> b >> c; v[a].push_back({ b,c }); v[b].push_back({ a,c }); } cin >> v1 >> v2; dijk(1); sToV1 = dist[v1]; sToV2 = dist[v2]; dijk(v1); V1ToV2 = dist[v2]; V1ToN = dist[N]; dijk(v2); V2ToN = dist[N]; res = min(res, sToV1 + V1ToV2 + V2ToN); res = min(res, sToV2 + V1ToV2 + V1ToN); if (V1ToV2 == INF || res == INF) cout << -1; else cout << res; }
✏️ 백준 1753
#include <iostream> #include <vector> #include <queue> #define INF 1000000 // 시작 노드에서 해당 노드까지의 경로가 없는 경우의 비용 #define MAX_VERTEX 20001 // 최대 vertex 개수 #define MAX_EDGE 300001 // 최대 edge 개수 using namespace std; // 최소 비용 배열 int d[MAX_VERTEX]; // 간선 정보를 담은 Vector 생성 // index : 시작 노드 // value : pair<비용, 도착 노드> 목록 vector<pair<int, int> > edge[MAX_EDGE]; void dijkstra(int start_node){ // 시작 노드에서 시작 노드로 가는 비용은 0 d[start_node] = 0; // 시작 노드부터 어떤 도착 노드까지의 최소 비용을 제시하는 간선 목록이며, // pair<비용, 도착 노드> 형식의 우선 순위 큐이다. priority_queue<pair<int, int> > pq; // 시작 노드에서 시작 노드로 가는 경로와 비용을 pq 에 삽입 pq.push(make_pair(0, start_node)); // pq 의 모든 경로들을 확인할 때까지 반복 while(!pq.empty()){ // 기존의 우선 순위 큐는, 첫 번째 값을 기준으로 큰 값이 top 에 오도록 정렬되어있다. // 하지만, 해당 알고리즘에선, 비용 값을 음수화 한 뒤 첫 번째 값으로 삽입하고, 도착 노드는 두 번째 값으로 삽입한다. // 따라서, 비용이 가장 작은 값이 top 에 오도록 정렬되어있다. // 즉, 가장 최소 비용을 주장하는 경로부터 확인하게 된다. // 시작 노드에서 어떤 도착 노드까지의 최소 경로를 주장하는 pq 의 top 에서, // 도착 노드를 현재 노드로 설정한다. int current = pq.top().second; // 시작 노드에서 현재 노드까지의 비용을 설정한다. // 비용은 음수화되어있는 상태이므로, 양수화해서 사용한다. int start_to_current_distance = -pq.top().first; // 현재 경로는 확인 되었으므로, 우선 순위 큐에서 제거한다. pq.pop(); // pq 의 top 에서 뽑은, 시작 노드부터 현재 노드까지의 비용과 // 최소 비용 배열에 있는, 시작 노드부터 현재 노드까지의 비용을 비교함으로써, // pq 의 top 에서 뽑은, 시작 노드부터 현재 노드까지의 비용이 더 크면 // 굳이 해당 경로를 통해 인접한 노드들을 확인할 필요가 없으므로, 더 이상 확인하지 않음 if (d[current] < start_to_current_distance){ continue; } // 상단 조건문에 걸리지 않고 통과하면, // 시작 노드부터 현재 노드까지는 최소 비용으로 이루어진 상태이므로, // 이제 현재 노드와 연결된 노드들을 모두 검사한다. for (int i=0; i<edge[current].size(); ++i){ // 다음 노드 설정 // 즉, 현재 노드와 i 번째로 인접한 노드 int next = edge[current][i].second; // 시작 노드에서 다음 노드까지의 비용 설정 // 즉, 시작 노드에서 현재 노드까지의 비용 + 현재 노드에서 i 번째로 인접한 노드까지의 비용 int start_to_next_distance = start_to_current_distance + edge[current][i].first; // 기존의, 시작 노드에서 다음 노드까지의 최소 비용보다 // 새롭게 계산한, 시작 노드에서 다음 노드까지의 비용이 더 작다면 // 최소 비용을 업데이트 if (d[next] > start_to_next_distance){ d[next] = start_to_next_distance; // 이제, 갱신된 경로가 최소 비용임을 주장하기 위해 // 우선 순위 큐에 해당 경로 삽입 pq.push(make_pair(-start_to_next_distance, next)); } } } } int main(){ // 노드의 개수와 간선의 개수 입력 int v, e; cin >> v >> e; // 시작 노드 입력 int start_node; cin >> start_node; // 최소 비용 배열 초기화 for (int i=1; i<v+1; ++i){ d[i] = INF; } // 간선 저장 for (int i=0; i<e; ++i){ // 시작 노드, 도착 노드, 비용 입력 int start, end, cost; cin >> start >> end >> cost; // 시작 노드에 따른 <비용, 도착 노드> 저장 edge[start].push_back(make_pair(cost, end)); } // 다익스트라 함수 실행 dijkstra(start_node); // 최소 비용 배열 출력 for (int i=1; i<v+1; ++i){ if (d[i] == INF){ cout << "INF" << " "; } else{ cout << d[i] << " "; } } return 0; }