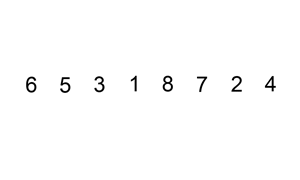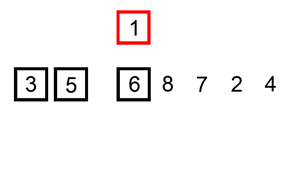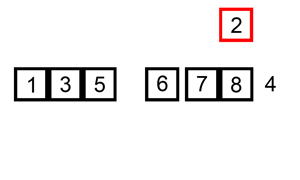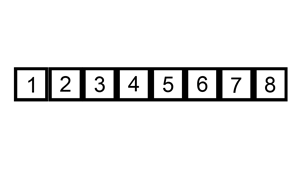
출처: Wikipedia
삽입 정렬은 두 번째 인자부터 시작하여 이전 요소들과 값을 비교한 후 적절한 위치를 찾아 삽입하는 방식으로 정렬을 진행합니다.
삽입 정렬도 이전에 다뤘던 버블, 선택 정렬과 마찬가지로 2중 반복문을 사용하지만 차이점이 있습니다.
바깥쪽 for문을 outer, 안쪽 for문을 inner라고 했을 때 버블정렬과 선택정렬은 outer 반복문의 반복시마다 최솟값 혹은 최댓값에 해당하는 요소의 최종위치가 확정되지만
삽입 정렬은 모든 정렬 과정이 끝나기 전까진 이동된 위치가 최종 위치라는 보장을 할 수 없습니다.
반복문이 돌면서 자신보다 이전에 위치한 값들을 기준으로만 위치가 결정되기 때문입니다.
구현
아래 로직은 오름차순 정렬을 기준으로 작성한 로직입니다.

function insertionSort(arr) {
// 비교할 대상이 있어야 하므로 두 번째 인자부터 반복을 진행합니다.
for(let i = 1; i < arr.length; i++) {
// key는 정렬 대상 요소, j는 비교 할 요소의 인덱스입니다.
let key = arr[i];
let j = i - 1;
// j가 요소의 끝인 0에 도달하거나, 현재 요소보다 작거나 같은 값을 만날때까지 반복합니다.
while(j >= 0 && arr[j] >= key) {
// 아직 타겟보다 작은 요소를 만나지 못했다면 이전 요소들을 뒤로 한칸씩 밀어줍니다.
arr[j+1] = arr[j];
j--;
}
// j가 이전 요소와의 비교를 위해 한칸 앞의 인덱스를 가르키고 있으므로
// j+1을 한 뒤 현재 값을 할당합니다.
arr[j+1] = key;
}
return arr;
}
console.log(insertionSort([5, 2, 4, 1, 3]));삽입 정렬은 최선은 Ω(n), 평균은 Θ(n^2), 최악은 O(n^2)의 시간복잡도를 가지며
정렬 과정에서 추가적인 공간을 요구하지 않으므로 공간복잡도는 O(1)입니다.
