문제

두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다.
정의를 확장해서, n개의 수의 최소공배수는 n 개의 수들의 배수 중 공통이 되는 가장 작은 숫자가 됩니다. n개의 숫자를 담은 배열 arr이 입력되었을 때 이 수들의 최소공배수를 반환하는 함수, solution을 완성해 주세요.

제한 사항

• arr은 길이 1이상, 15이하인 배열입니다.
• arr의 원소는 100 이하인 자연수입니다.

입출력 예

arr	result
[2,6,8,14]	168
[1,2,3]	6

정답

function solution(arr) {
    let answer = Math.max(...arr);

    while(true) {
        const isLCM = arr.every((n) => answer % n === 0);

        if (isLCM) return answer;

        answer++;
    }
}

풀이

제한사항이 타이트하지 않다고 느껴 최소공배수를 구하는 가장 간단한 방법으로 풀어보았습니다.

최소공배수를 구해야하므로 배열의 요소 중 가장 큰 값을 answer변수에 먼저 할당하고
반복시마다 answer의 값을 배열의 요소들로 나누었을 때 모두 나머지가 0이 나올 때까지 반복합니다.
만약 하나라도 나머지가 0이 아니라면 answer를 1씩 상승시키는 로직입니다.

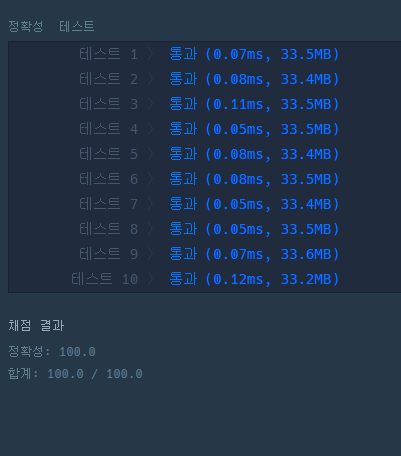
이 풀이는 코드가 간결하다는점은 좋았지만 성능 결과가 아래 사진과 같이 나와 몇몇 케이스에서 아쉬운 성능을 보여주었습니다.

리팩토링

위 풀이의 성능을 보완하기 위해 최대공약수를 구하는 알고리즘인 유클리드 호제법을 활용해보았습니다.
최소공배수는 두 수를 곱한값에 두 수의 최대공약수를 나누면 구할 수 있기 때문에 이를 활용하여 리팩토링을 진행해보았습니다.

function getGCD(a, b) {
    if (b === 0) return a;

    return getGCD(b , a % b);
}

function solution(arr) {
    let lcm = arr[0];
    
    for(let i = 1; i < arr.length; i++) {
        lcm = lcm * arr[i] / getGCD(lcm, arr[i]);
    }
    
    return lcm;
}

첫 번째 함수인 getGCD함수는 재귀적으로 b가 0이 될 때까지 호출되며 최종적으로 최대공약수를 반환합니다.

메인 함수인 solution함수에서는 for문을 통해 두 수를 차례로 비교하여 getGCD로 부터 반환받은 최대공약수를 활용해 최소공배수를 구하고 이를 lcm
변수에 할당합니다.

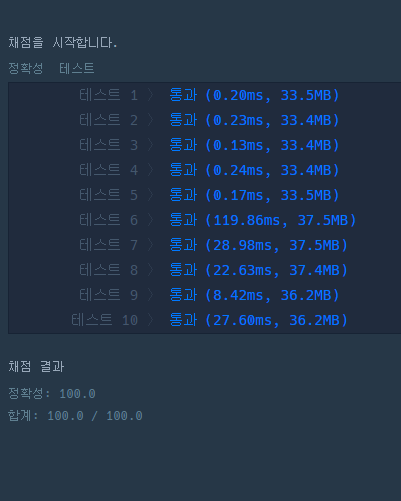
리팩토링 이후 아래 사진과 같이 개선된 성능 결과를 확인할 수 있었습니다.