시간복잡도
알고리즘이 문제를 해결하기 위한 연산의 횟수
버블 정렬(Bubble Sort)
0 ~ (N-1) 인접한 칸들을 비교하면서, 더 큰 수를 뒤로 보내는 방식입니다.
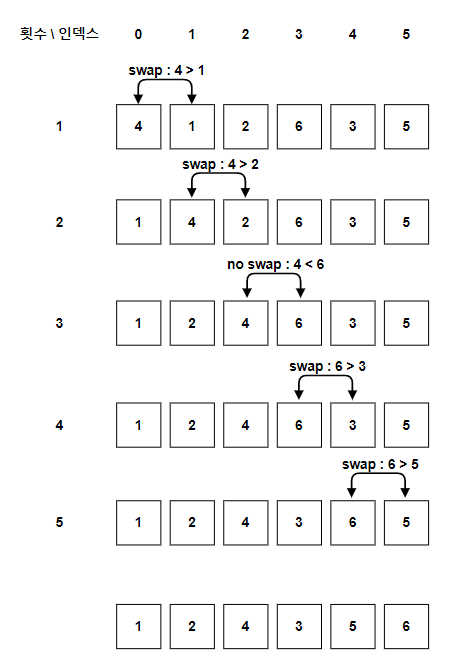
위의 그림은 [4, 1, 2, 6, 3, 5]을 버블 정렬하는 첫 번째 단계를 그림으로 표현한 것입니다.
버블 정렬은 인접한 수를 비교하면서 더 큰 수를 뒤로 보내는 방식이기 때문에 한 번 실행할 때마다, 가장 큰 수가 가장 뒤에 위치합니다.
따라서, 첫 번째 실행 후에는 가장 마지막 Index는 비교하지 않아도 됩니다.
시간 복잡도
총 실행 횟수 : N-1 + N-2 + N-3 ... + 1 = (N-1)N/2 = O(N^2)
N=6이라면, 5 + 4 + 3 + 2 + 1 = 15회 비교를 하게 됩니다.
버블 정렬은 최악/최선 모두 인접한 수를 처음부터 끝까지 비교해야하기 때문에 O(N^2)의 시간 복잡도를 가집니다.
선택 정렬(Selection Sort)
탐색을 시작하는 Index가 최소값을 가진다 가정하고, N-1까지 비교한 후에 0번째와 최소값의 위치와 swap하는 방식입니다. 탐색은 0번째 Index부터 시작합니다.
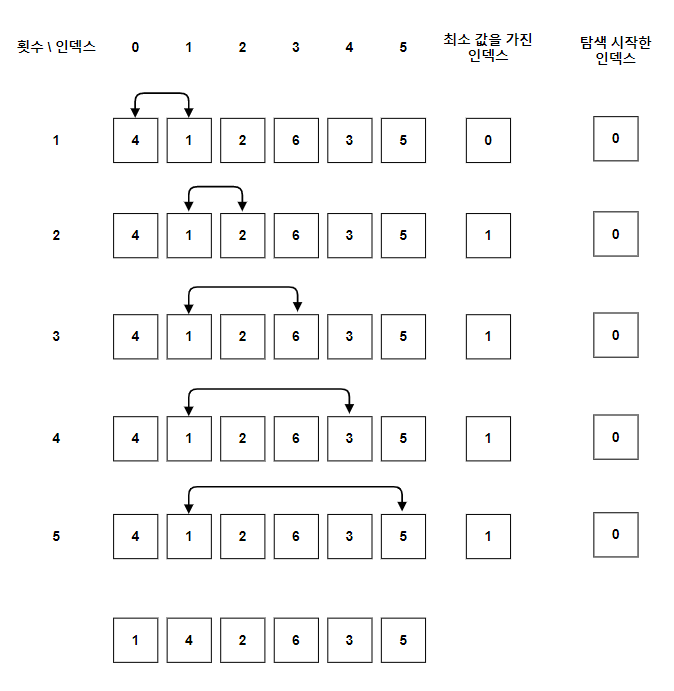
위의 그림은 [4, 1, 2, 6, 3, 5] 선택 정렬하는 첫 번째 단계를 그림으로 표현한 것입니다.
탐색을 시작하는 인덱스, 최소 값을 가진 인덱스를 저장할 공간이 필요합니다.
탐색은 0번째 Index부터 시작하고, 탐색을 시작하는 인덱스가 최소 값을 가진다. 가정하고 시작합니다.
선택 정렬은 최소값을 탐색을 시작했던, 가장 앞의 Index로 보내는 방식이기 때문에, 한 번 실행할 때마다, 가장 작은 수가 가장 앞에 위치합니다.
따라서, 첫 번째 실행 후에는 가장 앞의 Index는 비교하지 않아도 됩니다.
시간 복잡도
총 실행 횟수 : N-1 + N-2 + N-3 ... + 1 = (N-1)N/2 = O(N^2)
N=6이라면, 5 + 4 + 3 + 2 + 1 = 15회 비교를 하게 됩니다.
선택 정렬은 최악/최선 모두 가장 앞의 Index부터 끝까지 비교해야하기 때문에 O(N^2)의 시간 복잡도를 가집니다.
퀵 정렬(Quick Sort)
기준이 되는 Pivot의 위치를 찾아 Pivot보다 작은 수는 왼쪽, 큰 수는 오른쪽으로 분할해가며, 계속해서 좌/우의 Pivot위치를 찾아 정렬하는 방식입니다.

위의 그림은 [4, 1, 2, 6, 3, 5] 퀵 정렬 첫 번째 단계를 그림으로 표현한 것입니다.
- Low는 Pivot보다 큰 수를 찾을 때까지 Index를 1씩 증가시킵니다.
- High는 Pivot보다 작은 수를 찾을 때까지 Index를 1씩 감소시킵니다.
- 3번 처럼 Low는 Pivot보다 큰 수를, High는 Pivot보다 작은 수를 동시에 찾았으면, 둘의 값을 변경해줍니다.
- 4번 처럼 Low와 High가 엇갈리면, Pivot과 High의 위치를 swap해줍니다. Pivot이 swap된 위치(Index 3)는 고정입니다.
- 고정된 Pivot을 기준으로 왼쪽과 오른쪽으로 분할하여 위의 순서를 Left ~ Right의 길이가 0 또는 1이 될 때까지 반복해줍니다.
시간 복잡도
최선 : Pivot을 기준으로 정확하게 반으로 나눠진 경우 O(NlogN)
최악 : 이미 정렬된 리스트에 대하여 퀵 정렬하는 경우 O(N^2)
최선의 경우 설명
최악의 경우 설명
