[알고리즘] 최소 신장 트리(MST)

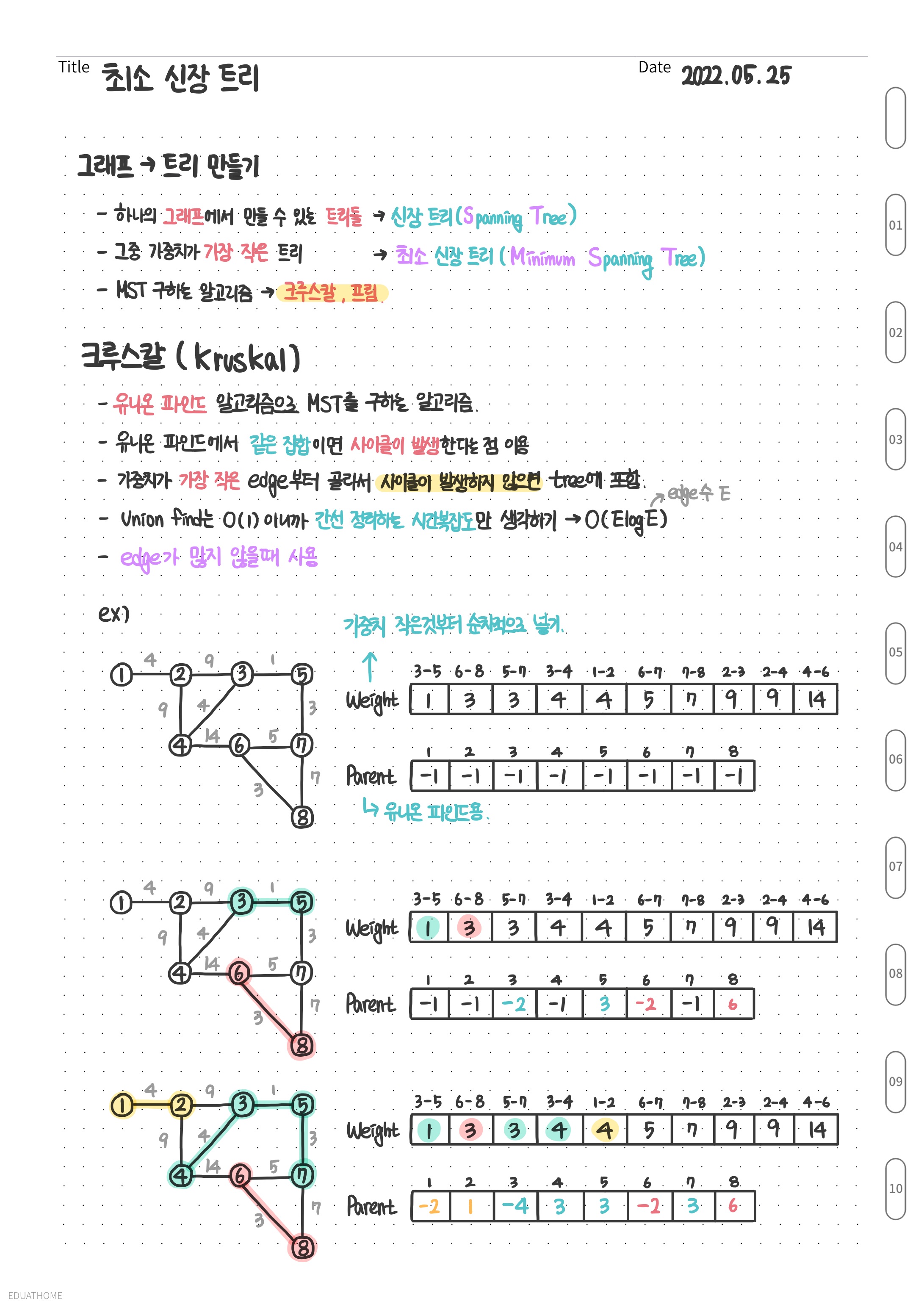
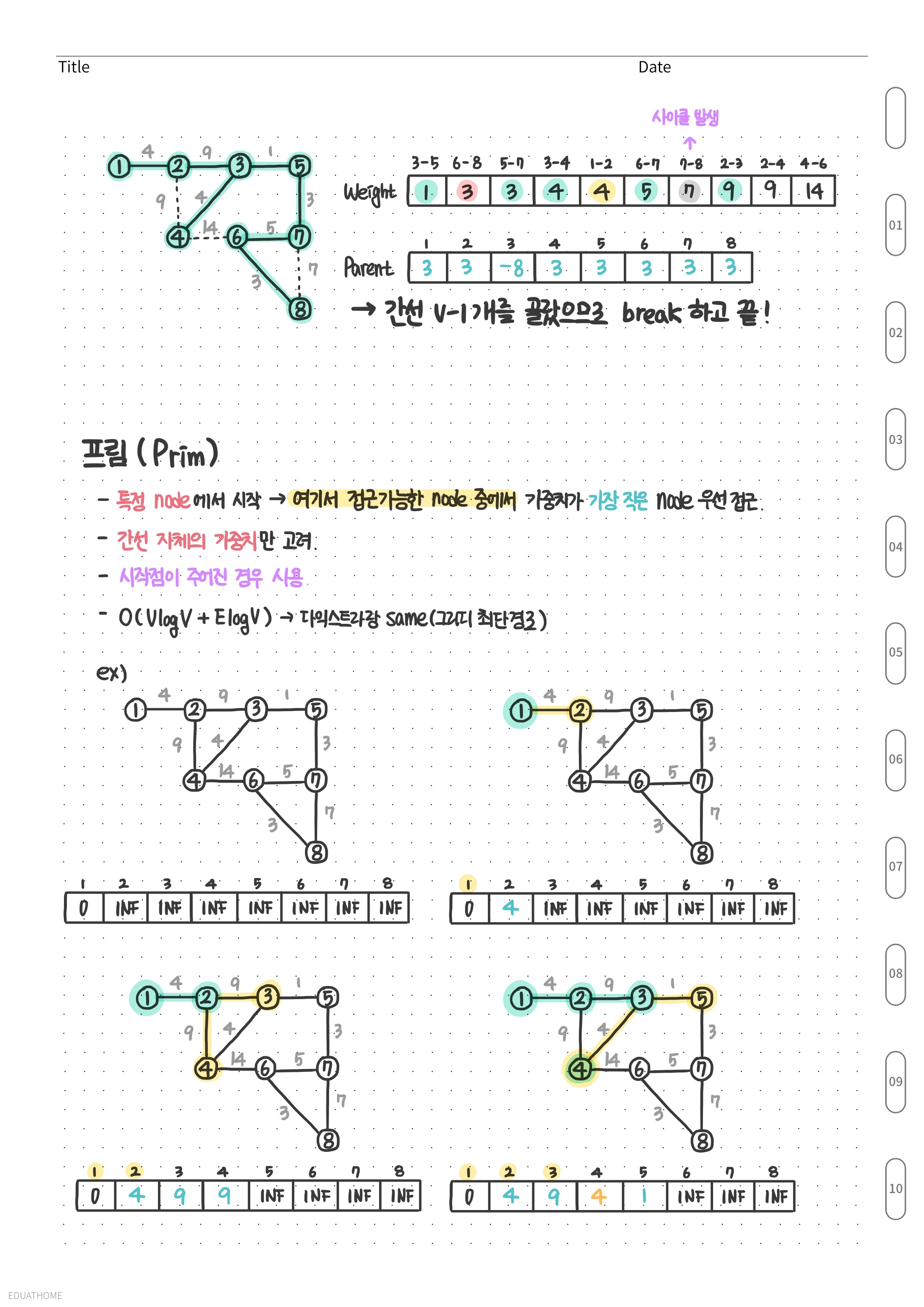
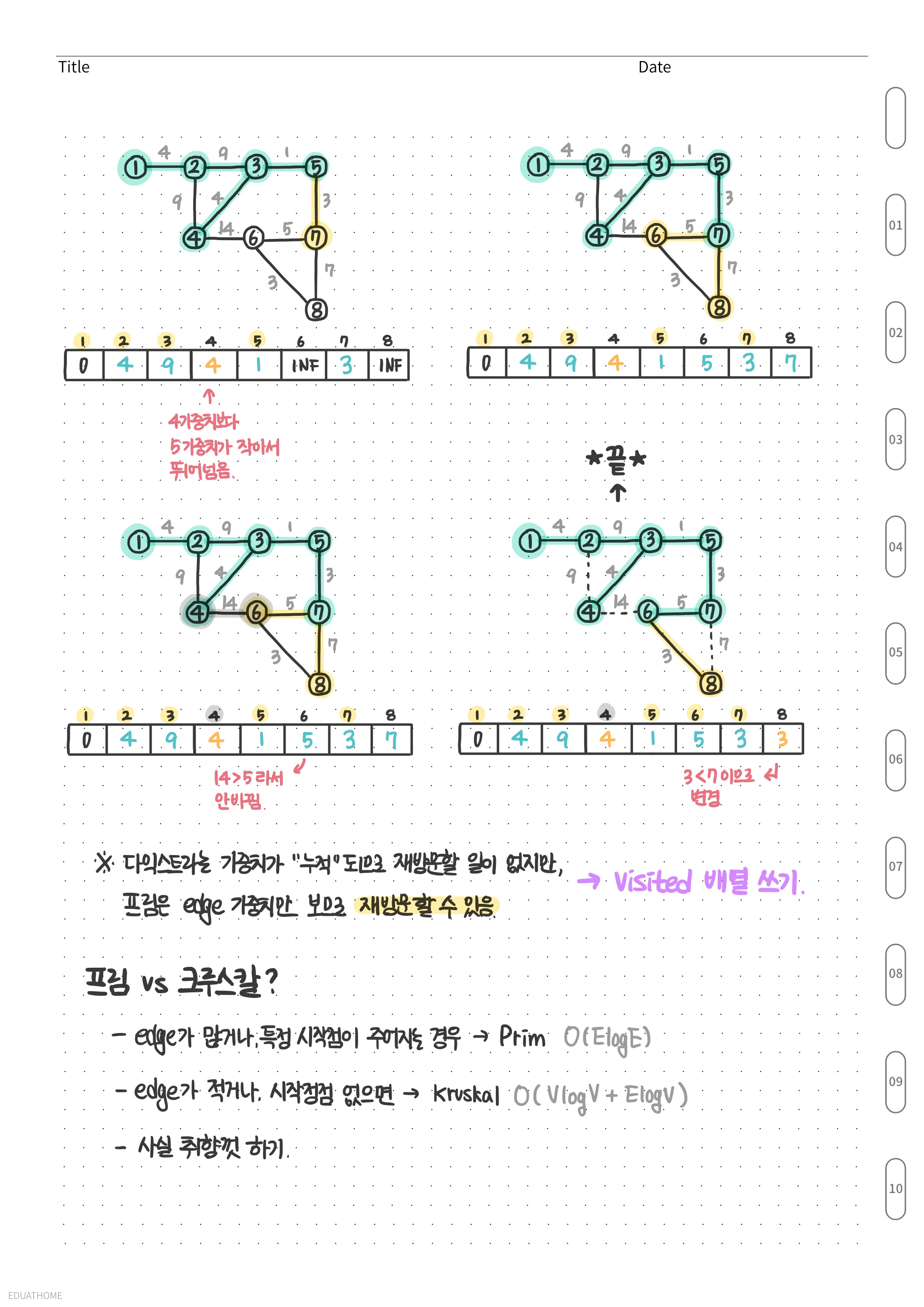
이론정리

문제풀이

#include <iostream>
#include <vector>
#include <tuple>
#include <queue>

//priority queue 사용해서 weight관리 - cmp파라미터에 greater<> 적으면 오름차순 정렬
using namespace std;
typedef tuple<int, int, int> tp;
vector<int> parent;

//유니온파인드 - find
int findParent(int node) {
    if(parent[node] < 0) {
        return node;
    }
    return parent[node] = findParent(parent[node]); //부모의 부모찾아서 root까지 찾았으면 그걸로 갱신해주기
}

//유니온파인드 - union
bool unionInput(int x, int y)
{
    int xp = findParent(x);
    int yp = findParent(y);

    if(xp == yp) return false;

    if(parent[xp] < parent[yp]) {
        parent[xp] += parent[yp]; //x쪽 트리에 y트리 노드들 갖다붙이기
        parent[yp] = xp; //x의 parent를 y부모의 parent로 붙여주기
    }
    else {
        parent[yp] += parent[xp];
        parent[xp] = yp;
    }
    return true;
}

//크루스칼(mst)
int kruskal (int v, priority_queue<tp, vector<tp>, greater<>> &pq) {
    int cnt = 0, sum = 0; //cnt는 사용한 간선 수

    while(cnt < v - 1) {
        int weight = get<0>(pq.top());
        int x = get<1>(pq.top());
        int y = get<2>(pq.top());
        pq.pop();

        //어차피 사이클이 생기는 경우에는 유니온 파인드가 알아서 false return할거임
        if(unionInput(x, y)) { //유니온파인드를 통해 한집단으로 합쳤다면
            cnt++;
            sum+=weight;
        }
    }
    return sum;
}

int main() {
    int v, e, a, b, c;
    priority_queue<tp, vector<tp>, greater<>> pq;

    cin >> v >> e;
    parent.assign(v+1, -1);
    while(e--) {
        cin >> a >> b >> c;
        pq.push({c, a, b}); //가중치를 맨앞에 둬서 그거 기준으로 오름차순 시키기
    }

    cout << kruskal(v, pq);
}