https://www.acmicpc.net/problem/15685

문제

드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다.
좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.

1. 시작 점
2. 시작 방향
3. 세대

0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다.
아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

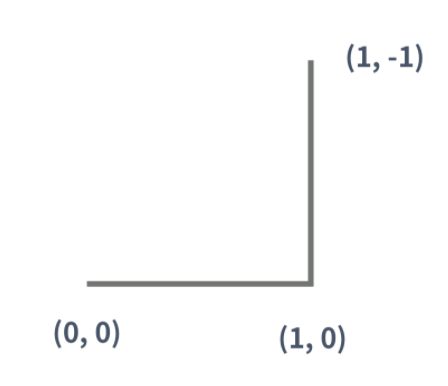
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

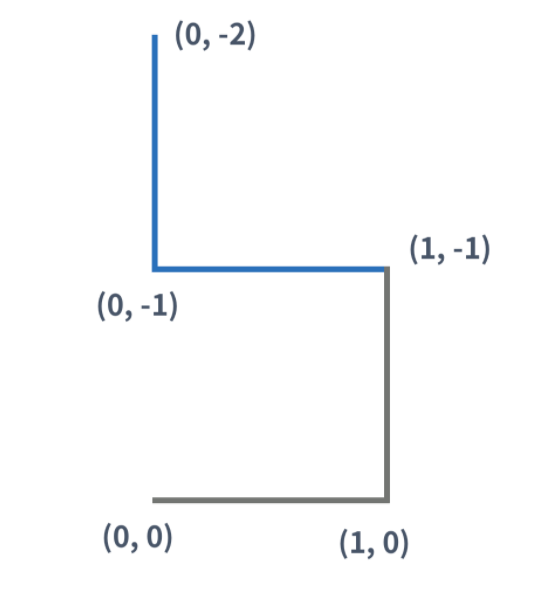
3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

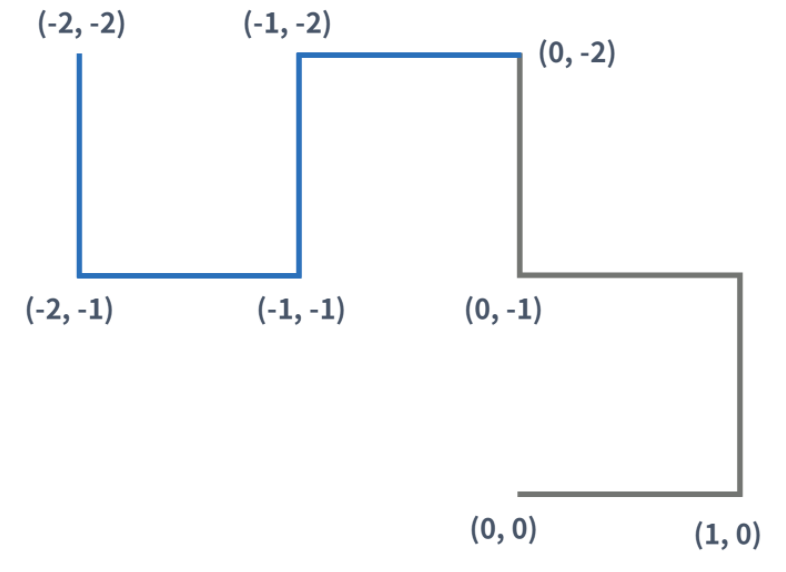
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.

크기가 100×100인 격자 위에 드래곤 커브가 N개 있다.
이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오.
격자의 좌표는 (x, y)로 나타내며,
0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.

---

입력

첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)

입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.

방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.

• 0: x좌표가 증가하는 방향 (→)
• 1: y좌표가 감소하는 방향 (↑)
• 2: x좌표가 감소하는 방향 (←)
• 3: y좌표가 증가하는 방향 (↓)

---

풀이

📍 풀이

• 드래곤 커브의 규칙을 찾는다.
  

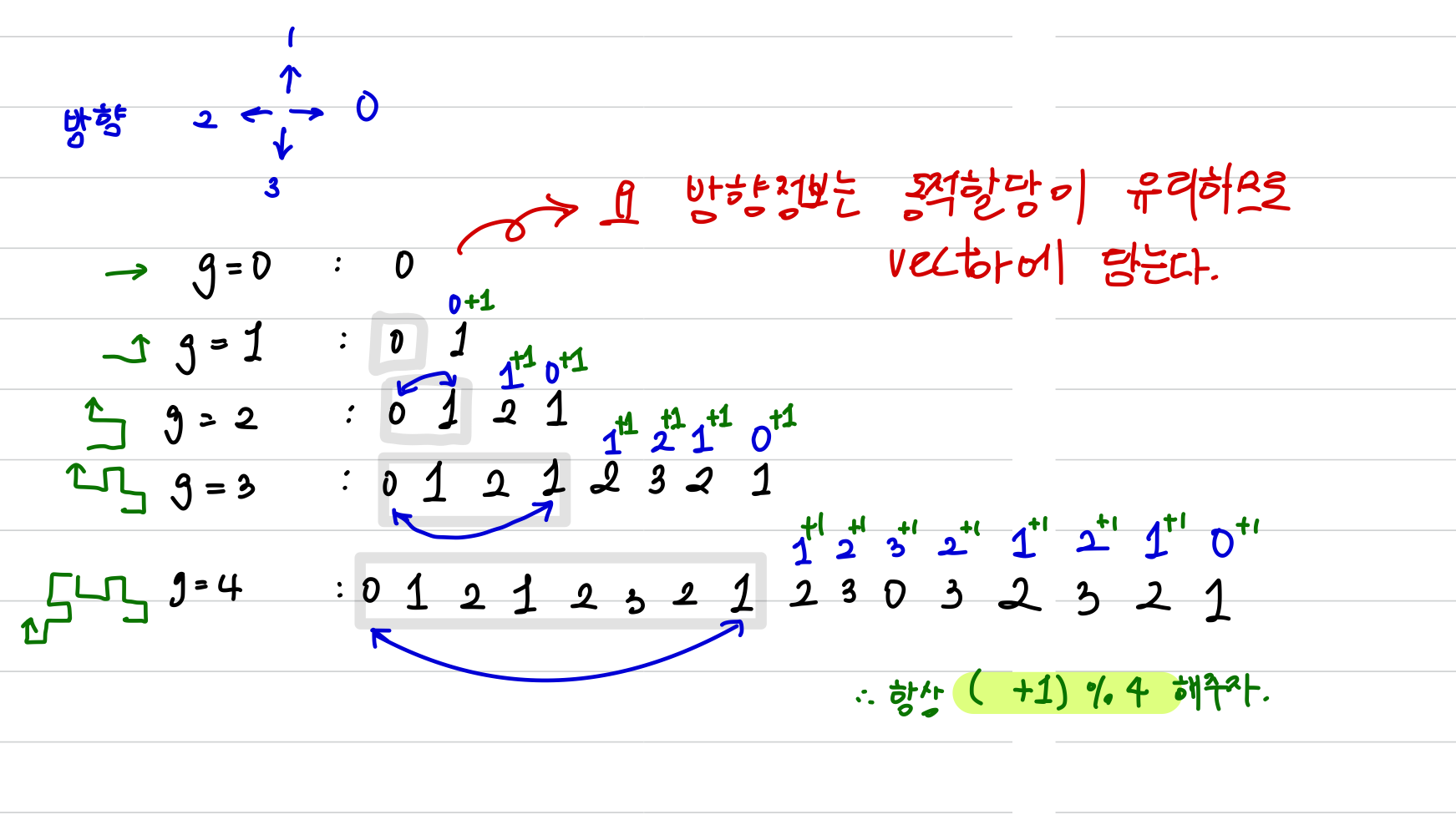
📍 코드

• 커브가 지나온 map은 1로 표시한다.
• 동적할당이 효율적인 상황이므로, 드래곤 커브를 array 대신 vector에 담는다.
• Make_Dragon_Curve()는 세대 수만큼 돌린다.

#include <iostream>
#include <vector>
using namespace std;
#define MAX 101

int N;
int x, y, d, g, cnt;
int map[MAX][MAX];
int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, -1, 0, 1 };
vector<int> direction;

void Make_Dragon_Curve()
{
    int size = direction.size();
    for (int i = size - 1; i >= 0; i--)
    {
        int temp = (direction.at(i) + 1) % 4;
        x += dx[temp];
        y += dy[temp];
        map[x][y] = 1;
        direction.push_back(temp);
    }
}

void Count_Square()
{
    for (int i = 0; i < MAX; i++)
    {
        for (int j = 0; j < MAX; j++)
        {
            if (map[i][j] == 1 && map[i][j + 1] == 1 && map[i + 1][j + 1] && map[i + 1][j] == 1)
                cnt++;
        }
    }
}

void Solution()
{
    cin >> N;

    while (N--)
    {
        direction.clear();
        cin >> x >> y >> d >> g;

        // initialize
        map[x][y] = 1;

        // generation 0
        x += dx[d];
        y += dy[d];
        map[x][y] = 1;
        direction.push_back(d);

        // next 'g' generations
        while (g--)
        {
            Make_Dragon_Curve();
        }
    }

    Count_Square();
    cout << cnt << endl;
}

int main()
{
    Solution();
}