👨‍💻 문제

---

✍️ 풀이

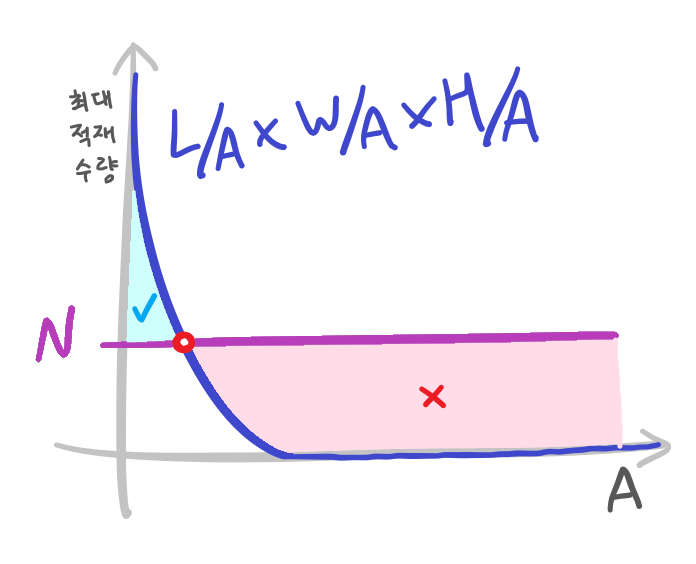
해당 문제를 좌표 평면에 표현하면 이렇다.
우리가 구해야하는 부분은 하늘색 부분 중 가장 오른쪽,
즉 교점에 가장 가까운 지점이다.

그럼 이제 여기서부터는 기본적인 이분탐색 문제다.

근데 엄청 많이 틀렸다.
원인은 실수에 있었다.

🔢 숫자 실수

    private static double bs(double left, double right) {

        if (right - left < 0.000000001) {
            return left;
        }

        double mid = (left + right) / 2;
        double midValue = getMaxPutAbleCount(mid);

        if (midValue < N) {
            return bs(left, mid);
        }
        else {
            return bs(mid, right);
        }

    }

값을 반환하는 조건에 좌우의 차이가 0.000000001보다 작다면이라는 조건을 걸었다.
이러한 조건을 걸었던 이유는 절대/상대 오차는 10^-9까지 허용한다.라는 내용 때문이었다.
최대한 오차가 적은 해답을 얻기 위함이었다.

하지만 안타깝게도 부동소수점의 한계로 해당 코드는 무한 루프를 돌게 되는 케이스가 존재한다.

그렇기에 무척이나 아쉽지만 그냥 최소한의 반복 횟수를 찾아 그만큼 반복시키기로 하였다.

A의 최대값은 L, W, H의 최대값, 즉 1,000,000,000이다.
절대/상대 오차는 10^-9까지 허용하므로 해당 숫자를 반으로 계속 쪼개서 0.000000001을 만들어보자.

public class Main {

    public static void main(String[] args) {
        double n = 1000000000;
        for (int i=1; n > 0.000000001f; i++) {
            n/=2;
            System.out.println(i+" : "+n);
        }
    }

}

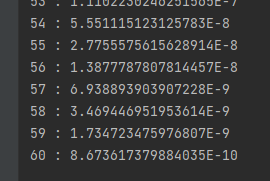
60번 도니까 0.000000001보다 같거나 작은 수가 만들어졌다.

그럼 어떤 수가 오든 최소 60번 이분탐색 돌리면 오차의 조건은 만들어진다.

    private static double bs(double left, double right) {
        for (int i=0; i<60; i++) {
            double mid = (left + right) / 2;
            double midValue = getMaxPutAbleCount(mid);

            if (midValue < N) {
                right = mid;
            }
            else {
                left = mid;
            }
        }
        return (left + right) / 2;
    }

😨 내 실수

근데도 틀렸다.

        System.out.println(bs(1, 1000000000));

그냥 어처구니가 없다.
무슨 생각으로 1로 시작을 했을까

이걸 발견 못 하고 혹시 이분탐색이 틀렸을까 몇 번이나 허우적거렸다.

        double maxA = Math.min(L, Math.min(W, H));
        System.out.println(bs(0, maxA));

고치니 맞았다.

추가로 최대 범위에 대한 제한을 주었다.
근데 지금 다시 생각해보니, 이거 고친다 한들 이분탐색 60번 도는 건 똑같다.
최적화가 되질 않는다.
그냥 1000000000으로 두어도 될 것 같다.

그게 아니라면 위에서 했던 것처럼 maxA를 0.000000001f보다 같거나 작은 값이 나올 때까지 반으로 쪼갠 다음, 해당 횟수를 사용하면 될 것 같다.

이는 장단점이 존재한다.
근데 그걸 또 만들어버리면 최적의 케이스에선 횟수가 감소하지만,
최악 케이스에서는 시간이 추가적으로 더 걸리게 된다.

또 다른 장점이라면 문제에서 제한하는 L, W, H의 최대값이 변하더라도 유동적으로 작동될 것이다.

---

📄 전체 소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class _1166 {

    private static int N;
    private static double L, W, H;

    public static void main(String[] args) throws IOException {
        StringTokenizer st = new StringTokenizer(new BufferedReader(new InputStreamReader(System.in)).readLine());
        N = Integer.parseInt(st.nextToken());
        L = Integer.parseInt(st.nextToken());
        W = Integer.parseInt(st.nextToken());
        H = Integer.parseInt(st.nextToken());

        System.out.println(bs(0, 1000000000));
    }

    private static double bs(double left, double right) {
        for (int i=0; i<60; i++) {
            double mid = (left + right) / 2;
            double midValue = getMaxPutAbleCount(mid);

//            System.out.println(left +"  ~  "+right);
            if (midValue < N) {
                right = mid;
            }
            else { // midValue >= N  :  mid가 답일수도 있음
                left = mid;
            }
        }
        return (left + right) / 2;
    }

    private static double getMaxPutAbleCount(double a) {
        return Math.floor(L/a) * Math.floor(W/a) * Math.floor(H/a);
    }
}

부동소수점은 괴롭다.