👨‍💻 문제

월드피자 원주 지점에서 N개의 피자 반죽을 오븐에 넣고 구우려고 한다.

그런데, 월드피자에서 만드는 피자 반죽은 지름이 제각각이다.

그런가하면, 월드피자에서 사용하는 오븐의 모양도 몹시 오묘하다.

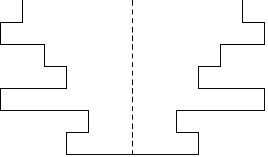
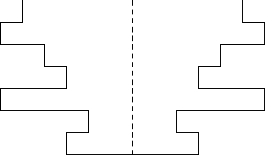
이 오븐은 깊은 관처럼 생겼는데, 관의 지름이 깊이에 따라 들쭉날쭉하게 변한다.

아래는 오븐의 단면 예시이다.

피자 반죽은 완성되는 순서대로 오븐에 들어간다.

이렇게 N개의 피자가 오븐에 모두 들어가고 나면, 맨 위의 피자가 얼마나 깊이 들어가 있는지가 궁금하다.

이를 알아내는 프로그램을 작성하시오.

⌨️ 입력

첫째 줄에 오븐의 깊이 D와 피자 반죽의 개수 N이 공백을 사이에 두고 주어진다. (1 ≤ D, N ≤ 300,000)

둘째 줄에는 오븐의 최상단부터 시작하여 깊이에 따른 오븐의 지름이 차례대로 주어진다.

셋째 줄에는 피자 반죽이 완성되는 순서대로, 그 각각의 지름이 주어진다.

오븐의 지름이나 피자 반죽의 지름은 10억 이하의 자연수이다.

🖨️ 출력

첫째 줄에, 마지막 피자 반죽의 위치를 출력한다.

오븐의 최상단이 1이고, 최하단 가장 깊은 곳이 D이 된다.

만약 피자가 모두 오븐에 들어가지 않는다면, 0을 출력한다.

📖 예제

입력

7 3
5 6 4 3 6 2 3
3 2 5

출력

2

---

✍️ 풀이

⌨️ 데이터 입력

	static int OvenDepth, PizzaCnt;
    static int[] Oven;
    static StringTokenizer Pizza;

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static void input() throws IOException {
        StringTokenizer st;

        st= new StringTokenizer(br.readLine());
        OvenDepth = Integer.parseInt(st.nextToken());
        PizzaCnt = Integer.parseInt(st.nextToken());

        Oven = new int[OvenDepth];
        st= new StringTokenizer(br.readLine());
        for(int i=0; i<OvenDepth; i++){
            Oven[i] = Integer.parseInt(st.nextToken());
        }

        Pizza = new StringTokenizer(br.readLine());
    }

    public static void resizeOven(){
        for(int i=1; i<OvenDepth; i++){
            Oven[i] = Math.min(Oven[i], Oven[i-1]);
        }
//        for(int i=0; i<OvenDepth; i++)
//            System.out.printf("%3d",Oven[i]);
//        System.out.println();
    }

단순히 입력받는다.
오븐의 지름들은 그대로 배열에 저장한다.
피자들의 문자열 은 StringTokenizer에 저장하여 이후 큐와 같이 작동하며 결과값을 도출해낼 것이다.

---

🎛️ 오븐 지름 바꾸기

    public static void resizeOven(){
        for(int i=1; i<OvenDepth; i++){
            Oven[i] = Math.min(Oven[i], Oven[i-1]);
        }
//        for(int i=0; i<OvenDepth; i++)
//            System.out.printf("%3d",Oven[i]);
//        System.out.println();
    }

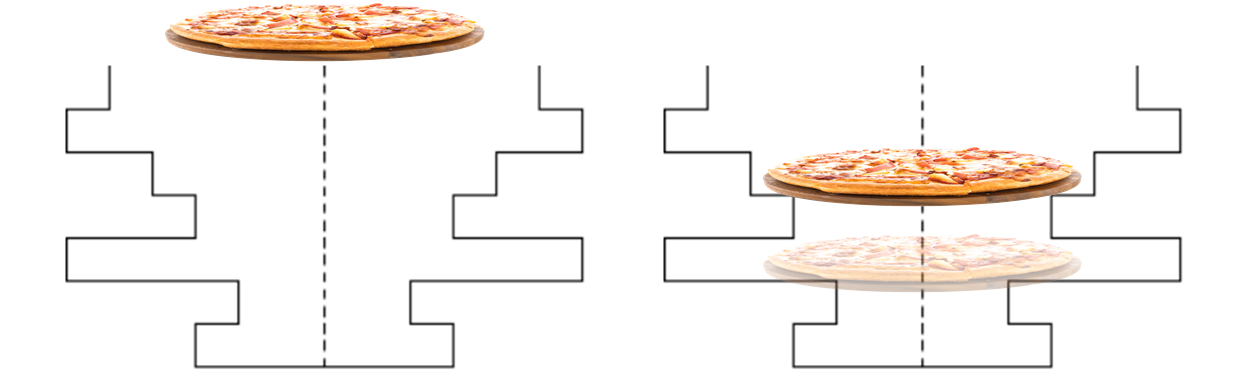
피자는 위에서 밑으로 떨어진다.

피자는 지름이 충분한 공간이 있다고 하더라도
그 공간 위에 지름이 좁은 공간이 있다면 지름이 충분한 공간을 차지할 수 없다.

그러므로 오븐의 지름들의 값을 이래과 같이 저장한다.

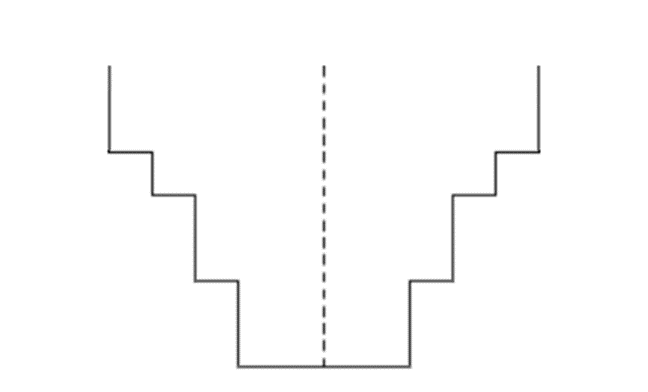
5 6 4 3 6 2 3 👉 5 5 4 3 3 2 2

---

🍕 피자 떨어뜨리기

큐에 담긴 피자들을 떨어뜨리며 결과값을 도출해낸다.

1. 피자는 오븐의 빈 공간 중 가장 낮은 피자의 크기 이상의 공간에 놓인다.

2. 피자가 놓여진 공간 이하의 공간들은 전부 놓을 수 없는 공간이 된다.
   그 위에 있는 공간만을 빈 공간이라고 생각한다.

위 과정을 피자가 놓일 수 없을 때 혹은 피자를 모두 놓을 때까지 반복한다.

이 과정에서 투포인터를 사용하여도 좋고 이분탐색을 사용하여도 좋다.
필자는 이분탐색을 활용하였다.

    public static int getResult(){
        int lastOvenFloor = OvenDepth;

        for(int i=0; i<PizzaCnt; i++){
            int pizza = Integer.parseInt(Pizza.nextToken());
            lastOvenFloor = searchPlaceableDepth( pizza, 0, lastOvenFloor-1 );
//            System.out.println(lastOvenFloor+'\n');
            if(lastOvenFloor == -1) break;
        }

        return lastOvenFloor + 1;
    }

    public static int searchPlaceableDepth(int pizza, int high, int low){
//        System.out.printf("%d -> %d~%d\n",pizza,high,low);
        if( low<0 ) return -1;
        if( pizza>Oven[high] ) return -1;
        if( pizza<=Oven[low] ) return low;

        int mid = (high+low)/2;
        if( Oven[mid]>=pizza && Oven[mid+1]<pizza ) return mid;
        else if( pizza > Oven[mid] ) return searchPlaceableDepth(pizza, high, mid-1);
        else return searchPlaceableDepth(pizza, mid, low);
    }

lastOvenFloor의 초기값은 오븐의 밑바닥이며, 피자를 놓을 때마다 피자가 놓인 높이로 갱신된다.
해당 변수를 기준으로 이하는 놓을 수 없는 공간, 그 위는 빈 공간으로 판단한다.
결과값 역할 또한 수행한다.

---

📄 전체 소스코드

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) throws IOException {
        input();
        resizeOven();
        System.out.println(getResult());
    }

    static int OvenDepth, PizzaCnt;
    static int[] Oven;
    static StringTokenizer Pizza;

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static void input() throws IOException {
        StringTokenizer st;

        st= new StringTokenizer(br.readLine());
        OvenDepth = Integer.parseInt(st.nextToken());
        PizzaCnt = Integer.parseInt(st.nextToken());

        Oven = new int[OvenDepth];
        st= new StringTokenizer(br.readLine());
        for(int i=0; i<OvenDepth; i++){
            Oven[i] = Integer.parseInt(st.nextToken());
        }

        Pizza = new StringTokenizer(br.readLine());
    }

    public static void resizeOven(){
        for(int i=1; i<OvenDepth; i++){
            Oven[i] = Math.min(Oven[i], Oven[i-1]);
        }
//        for(int i=0; i<OvenDepth; i++)
//            System.out.printf("%3d",Oven[i]);
//        System.out.println();
    }

    public static int getResult(){
        int lastOvenFloor = OvenDepth;

        for(int i=0; i<PizzaCnt; i++){
            int pizza = Integer.parseInt(Pizza.nextToken());
            lastOvenFloor = searchPlaceableDepth( pizza, 0, lastOvenFloor-1 );
//            System.out.println(lastOvenFloor+'\n');
            if(lastOvenFloor == -1) break;
        }

        return lastOvenFloor + 1;
    }

    public static int searchPlaceableDepth(int pizza, int high, int low){
//        System.out.printf("%d -> %d~%d\n",pizza,high,low);
        if( low<0 ) return -1;
        if( pizza>Oven[high] ) return -1;
        if( pizza<=Oven[low] ) return low;

        int mid = (high+low)/2;
        if( Oven[mid]>=pizza && Oven[mid+1]<pizza ) return mid;
        else if( pizza > Oven[mid] ) return searchPlaceableDepth(pizza, high, mid-1);
        else return searchPlaceableDepth(pizza, mid, low);
    }
}

---

💡 최적화

서술한 방식은 오븐의 지름들을 단순한 int배열로 저장한다.
7 7 7 7 7 7 7 6 6 6 6 6 6 5 5 5 5 5 4 4 4 4 3 3 3 3 3 2 2 2 2 2 2 1 1 1 1 1 1 1

배열이 아닌 객체 리스트로 저장하면 탐색 시간을 조금 더 줄일 수 있게 된다.

객체

index	지름	갯수
0	7	7
1	6	6
2	5	5
3	4	4
4	3	5
5	2	6
6	1	7

지름과 해당 지름의 갯수를 저장한 객체로 리스트를 구현하면 이분탐색의 탐색 횟수를 줄일 수 있다.

피자가 놓일 때마다 해당하는 지름의 갯수를 1씩 뺀다.

결과값인 피자가 놓인 마지막 위치는 남아있는 빈 공간을 선형으로 탐색하며 더하면 구해낼 수 있다.

위치값 저장

결과값을 구하는 시간마저 아깝다면 객체에 실제 위치를 저장한다.

index	지름	갯수	가장 높은 위치
0	7	7	1
1	6	6	8
2	5	5	14
3	4	4	19
4	3	5	23
5	2	6	28
6	1	7	34

피자가 놓인 마지막 위치는 해당 지름의 가장 높은 위치 + 갯수를 통해 구해낼 수 있다.