👨‍💻 문제

---

✍️ 풀이

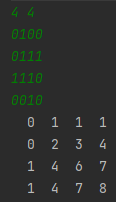
📈 누적합

2차원 배열에서 (a,b)부터 (c,d)까지의 총합은 누적합을 활용하면 빠르게 구할 수 있다.

    private static void prefixSum() {
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                arr[r][c] += arr[r-1][c];
            }
        }
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                arr[r][c] += arr[r][c-1];
            }
        }
    }

🧮 사각형의 넓이

누적합은 (0,0)에서부터 (x,y)까지의 총합을 빠르게 구해낼 수 있다.

(3,3)에서부터 (4,4)까지의 총합을 구하고 싶다면,
위 그림과 같이 파란 구역에서 필요없는 부분인 노란 구역과 빨간 구역을 뺀 후에,
중복으로 뺀 부분인 녹색 구역을 한 번 더해준다.
8 - 4 - 4 + 2

    private static int getSize(int r, int c, int length) {
        return arr[r-1+length][c-1+length] - arr[r-1][c-1+length] - arr[r-1+length][c-1] + arr[r-1][c-1];
    }

해당 문제에서 구하는 형태는 무조건 정사각형이기에,
2개의 좌표가 아닌 시작 좌표와 한 변의 길이를 매개변수로 사용하였다.

💪 최댓값

각 좌표를 선형으로 돌며, 최댓값을 찾아 반환한다.

이때, 불필요한 연산은 최대한 줄여야 한다.
모든 좌표에서 모든 넓이를 확인한다면 대참사다.

첫째로, 해당 좌표에서 임의의 크기가 정사각형이 아니라면, 더 큰 크기는 정사각형일 수 없다.

1 1 1 1
1 1 1 1 
1 1 0 1
1 1 1 1

위 형태에서 3*3이 정사각형이 아니라면 4*4 또한 정사각형이 될 수 없다.
아래 코드에서는 break가 그 역할을 한다.

둘째로, 최대값을 저장한다.
만약 다른 좌표에서 정사각형의 최대값을 3이라고 측정했다면,
또 다른 좌표들에서는 굳이 3이하의 정사각형은 확인할 필요가 없다.
아래 코드에서는 length가 그 역할을 한다.

    private static int getMaxSize() {
        int length = 0;
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                for (int l=length; r+l<=R && c+l<=C; l++) {
                    if (isSquare(r, c, l + 1)) {
                        length++;
                    }
                    else {
                        break;
                    }
                }
            }
        }
        return length * length;
    }

---

📄 전체 소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class _1915 {

    private static int R, C;
    private static int[][] arr;

    public static void main(String[] args) throws IOException {
        input();
        prefixSum();
        System.out.println(getMaxSize());
    }

    private static void input() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        R = Integer.parseInt(st.nextToken());
        C = Integer.parseInt(st.nextToken());

        arr = new int[R+1][C+1];
        for (int r=1; r<=R; r++) {
            String str = br.readLine();
            for (int c=1; c<=C; c++) {
                arr[r][c] = str.charAt(c-1) - '0';
            }
        }
    }

    private static void prefixSum() {
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                arr[r][c] += arr[r-1][c];
            }
        }
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                arr[r][c] += arr[r][c-1];
//                System.out.printf("%3d", arr[r][c]);
            }
//            System.out.println();
        }
    }

    private static int getMaxSize() {
        int length = 0;
        for (int r=1; r<=R; r++) {
            for (int c=1; c<=C; c++) {
                for (int l=length; r+l<=R && c+l<=C; l++) {
                    if (isSquare(r, c, l + 1)) {
                        length++;
                    }
                    else {
                        break;
                    }
                }
            }
        }
        return length * length;
    }

    private static boolean isSquare(int r, int c, int length) {
        return getSize(r, c, length) == length * length;
    }

    private static int getSize(int r, int c, int length) {
        return arr[r-1+length][c-1+length] - arr[r-1][c-1+length] - arr[r-1+length][c-1] + arr[r-1][c-1];
    }

}