[백준] 2133. 타일 채우기 (Java)

서재·2024년 2월 27일

Java 다이나믹 프로그래밍 백준 알고리즘

백준 JAVA 풀이

목록 보기

22/36

👨‍💻 문제

✍️ 풀이

높이가 3이었기에 풀기에 조금 원활했던 문제였다.

🤔 생각

우선 2*1 타일로 만들 수 있는 직사각형들을 구상했다.

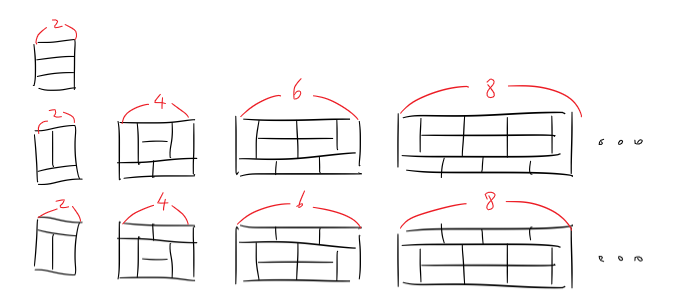
그 결과 위와 같이,
너비가 2인 직사각형 1개와,
너비가 2씩 증가하는 직사각형들의 집합 2개가 있음을 알아내었다.

이제 2*1 타일은 갖다 버리고 위 조각들로 퍼즐을 맞춘다고 생각한다.

📈 DP

현재 너비까지 만들 수 있는 경우의 수를
위 직사각형들이 도달하는 곳에 더해준다.

        for (int i = 0; i + 2 <= N; i += 2) {
            arr[i + 2] += arr[i];                 // 너비가 2인 직사각형 1개
            for (int j = i + 2; j <= N; j += 2) {
                arr[j] += 2 * arr[i];             // 너비가 2씩 증가하는 직사각형들의 집합 2개
            }
        }

📄 전체 소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N + 1];
        arr[0] = 1;

        for (int i = 0; i + 2 <= N; i += 2) {
            arr[i + 2] += arr[i];
            for (int j = i + 2; j <= N; j += 2) {
                arr[j] += 2 * arr[i];
            }
        }

        System.out.println(arr[N]);
    }

}