본 게시글은 [링크] 해당 강의를 정리한 글입니다.
📕 동적 계획법이란
- 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법
- 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다.
- 다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(탑 다운과 보텀 업)으로 구성
- 이름엔 별 의미가 없다.
🔽 해당 조건을 만족할 때 (효율적으로)사용할 수 있다.
1 최적 부분 구조 (Oprimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
2 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야 한다.
💻 예제 - 피보나치 수열
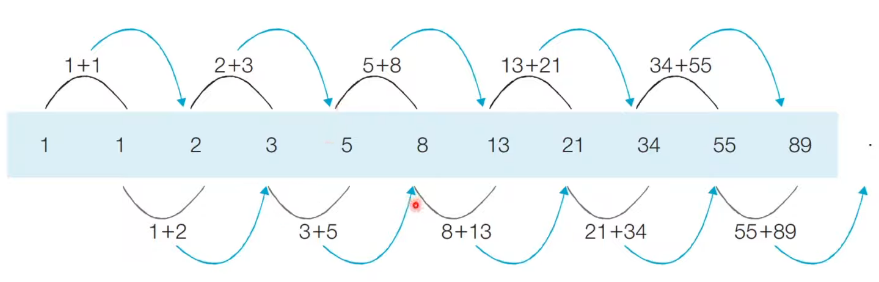
1 재귀만 사용한 code ➡️ 계산의 중복 실행
public static int recur(int num) {
if ( num <= 2) return 1;
return recur(num - 1) + recur(num - 2);
}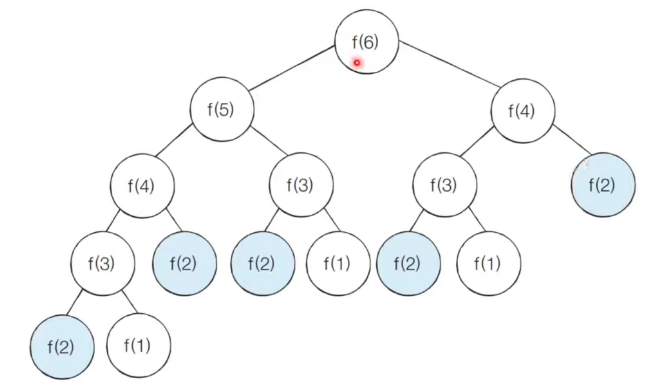
- f(6)을 구하는데 여러 함수가 중복적으로 실행되고 있다.
- ex) f(2)가 5번이나 중복되는 것을 볼 수 있다
- O() 의 복잡도를 가진다.
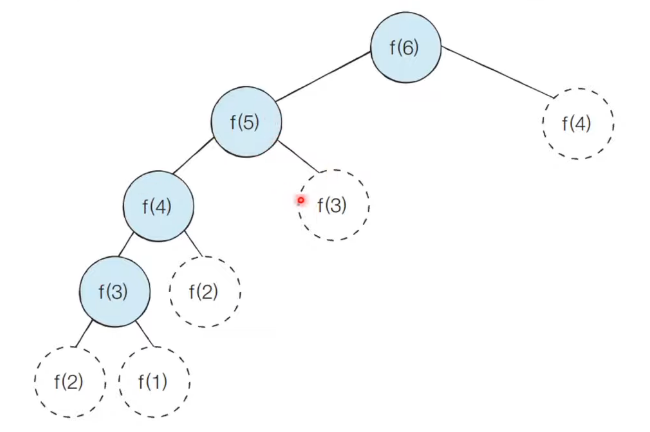
2 동적 계획법으로 구현 했을 때의 함수 호출
// 바텀업 동적계획법으로 구현
public static long dinamicFibo(int n) {
long [] table = new long [n + 1];
table[0] = 0;
table[1] = 1;
for (int i = 2; i <= n; i++) {
table[i] = table[i-1] + table[i-2];
}
return table[n];
}
// 탑다운 동적계획법으로 구현
public static long dp(int n, long [] memo) {
if (n <= 1) {
return n;
} else if (memo[n] != 0) {
return memo[n];
} else {
return memo[n] = dp( n -1, memo) + dp(n -2, memo);
}
}
3 코드 실행 시 , 각 방법의 속도 비교
n = 50;
1. 재귀
실행시간 : 74.403초
2. DP (바텀업)
실행시간 : 0.0초
3. DP (탑다운)
실행시간 : 0.0초
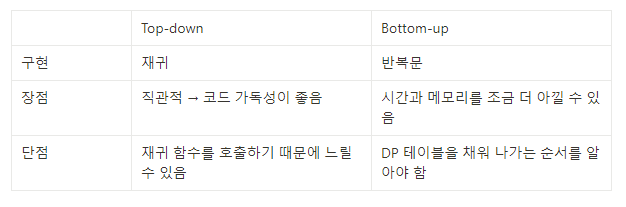
📕 동적계획법의 두가지 방법
⬛ 탑-다운 (하향식)
- 구현에서 재귀를 이용한다.
- 작은 문제들을 재귀적으로 호출하여 그 작은 문제들이 해결되면 큰 문제가 해결되는 과정이다.
- 작은 문제를 기록하기 위해 메모이제이션기법을 이용한다.
* 메모이제이션 (Memoization)
: 한 번 계산한 결과를 메모리 공간에 메모하는 기법
⬛ 보텀-업 (상향식)
- 아래서 부터 작은 문제들을 풀고, 큰 문제를 차근히 푼다.
- for문을 이용한다.
- 동적 계획법의 전형적인 형태는 이 보텀업 방식이다.
- 결과 저장용 리스트는 DP 테이블이라고 부른다.
📕 동적 계획법 vs 분할 정복
공통점
- 최적 부분 구조를 가질 때 사용한다.
차이점
- 부분 문제의 중복
- DP 문제는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복된다.
- 분할 정복문제는 동일한 부분 문제가 반복적으로 계산되지 않는다 ex) 퀵정렬
💡 코테 Tip - DP 문제에 접근하는 방법
1 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 검토한다.
2 아이디어가 없다면 DP로 풀것을 고려한다.
3 재귀함수로 비효율적인 완전 탐색 프로그램을 작성한다. 탑다운(하향식)
4 작은문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 쓴다.
➡️ 익숙하지 않으면 어렵다. 많이 풀어봐야한다.
