[python] 백준 1735번

안녕하세요 !

오늘은 백준 - 분수 합 문제를 가지고 왔습니다.

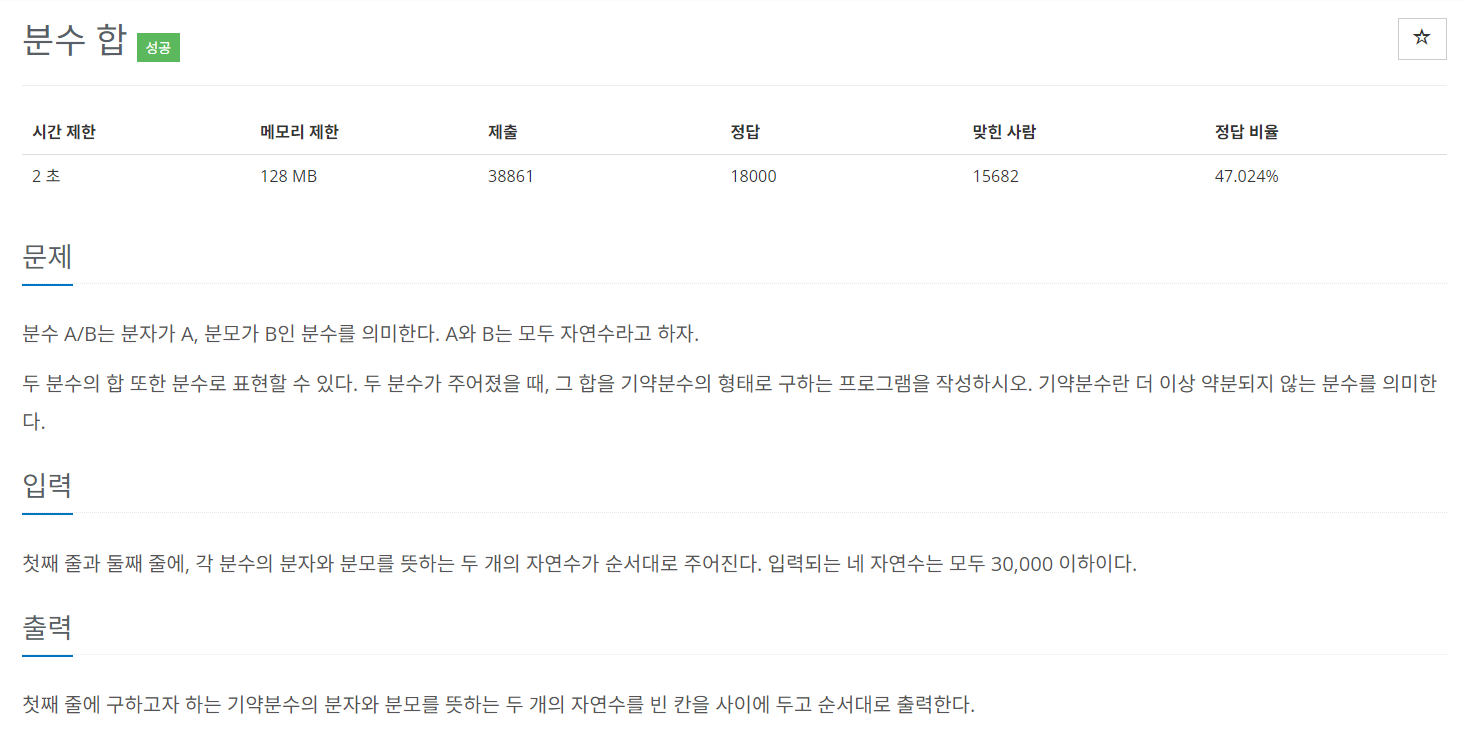
문제 설명

해결 방법

문제를 해결할 때 최대공약수를 구하는 유클리드 호제법을 사용했습니다. 아래는 최대공약수를 구하는 함수입니다.

def gcd(a, b):
    c = -1
    while 1:
        c = a % b
        if not c:
            return b
        a = b
        b = c

두 수 a, b의 최대공약수로 최소공배수를 구하는 방법은 아래와 같습니다.

최소공배수 = a * b / 최대공약수

문제를 해결한 방법을 아래에 정리해보겠습니다.

1. 입력을 받습니다.
2. 두 분모의 최대공약수를 구합니다.
3. 두 분수 합의 분모와 분자를 구해줍니다.
4. 두 분수 합의 분모와 분자 사이의 최대공약수를 구해줍니다.
5. 기약분수를 구해줍니다.

1. 입력을 받습니다.

arr = list(map(int, sys.stdin.readline().strip().split()))
arr2 = list(map(int, sys.stdin.readline().strip().split()))

2. 두 분모의 최대공약수를 구합니다.

number = 0
if arr2[1] >= arr[1]:
    number = gcd(arr2[1], arr[1])
else:
    number = gcd(arr[1], arr2[1])

3. 두 분수 합의 분모와 분자를 구해줍니다.

denom = arr[1] * arr2[1] // number
num = (denom // arr[1]) * arr[0] + (denom // arr2[1]) * arr2[0]

4. 두 분수 합의 분모와 분자 사이의 최대공약수를 구해줍니다.

number2 = gcd(denom, num)

5. 기약분수를 구해줍니다.

print(f"{num//number2} {denom//number2}")

전체 코드

import sys

def gcd(a, b):
    c = -1
    while 1:
        c = a % b
        if not c:
            return b
        a = b
        b = c

arr = list(map(int, sys.stdin.readline().strip().split()))
arr2 = list(map(int, sys.stdin.readline().strip().split()))

number = 0
if arr2[1] >= arr[1]:
    number = gcd(arr2[1], arr[1])
else:
    number = gcd(arr[1], arr2[1])

denom = arr[1] * arr2[1] // number
num = (denom // arr[1]) * arr[0] + (denom // arr2[1]) * arr2[0]

number2 = gcd(denom, num)

print(f"{num//number2} {denom//number2}")