[강의 정리] Deep Metric Learning

고려대학교 DMQA Youtube "Deep Metric Learning" 영상을 보고 정리한 글입니다.

정의

• Deep Metric Learning에서
  Metric이란 Distance(거리)로 생각하면 됨
  Deep = Deep Neural Network
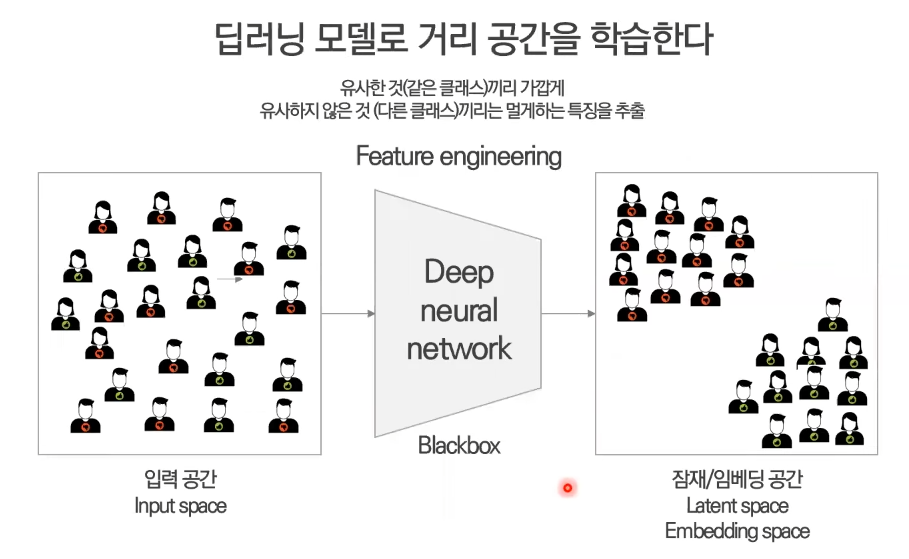
  = 딥러닝 모델로 거리 공간을 학습한다

• 거리는 다음 조건을 만족하는 함수를 의미 (D라고 표현)
  - D(x,y) = 0 : 자기 자신과의 거리는 0이다.
  - D(x,y) = D(y,x) : 거리는 상호 대칭성을 가진다.
  - D(x,y) $\le$ D(x,z) + D(z,y) : 거리는 삼각부등식을 만족한다.
  

• 자주 쓰이는 거리 함수의 종류
  

• 거리 공간 (metric space)는 두 개체 사이의 거리가 정의된 공간
  = 유사한 개체는 가까이, 유사하지 않은 개체는 멀리 위치한 공간

예시

• KNN
  "X가 유사하면 y도 유사하다"라고 가정
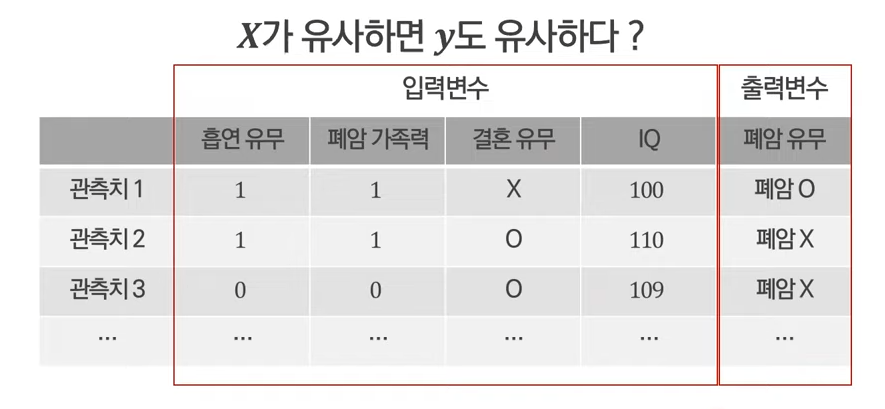  X로 유사도가 계산돼서 y가 결정됨
  하지만 결혼 유무, IQ는 폐암과 관련없는 변수!! => 이러한 변수까지도 포함되어 거리가 계산됨
  
  
  → "X가 유사하면 y도 유사하다"는 옳지 않음!
  → 모든 변수(X)들이 동일한 중요도로 거리가 계산됨

그렇다면?

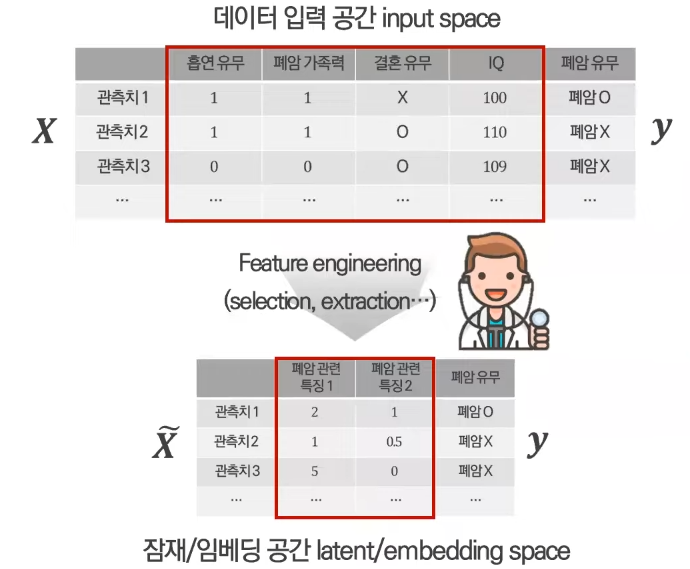
y에 대한 잠재적인 의미를 포함하고 있을만한 feature들을 뽑음
하지만 최근 데이터들의 형태 = 변수의 수가 많은 정형데이터, 이미지나 신호같은 비정형 데이터
→ 특징 추출하기가 어려움 → DNN으로 해결

Deep Metric Learning

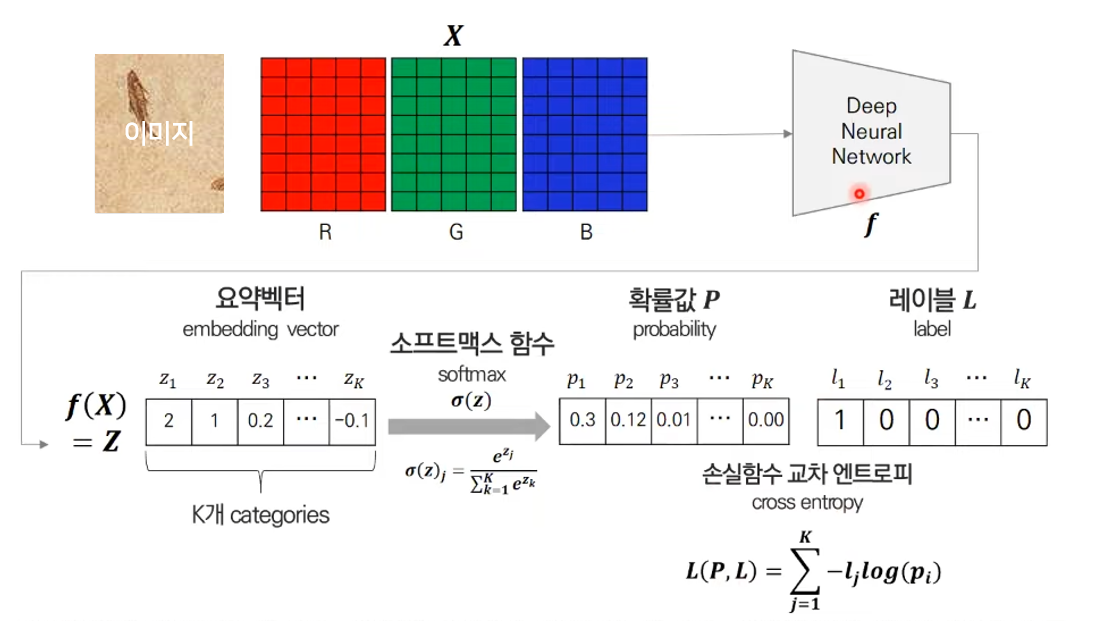
• 어떤 손실함수를 써야할까?

1) Face Recogntion 분야에서 Softmax classifier로 학습된 feature의 한계
아래와 같이 학습이 되고,

Softmax Classifier를 통해 학습된 feature는 다음과 같다.

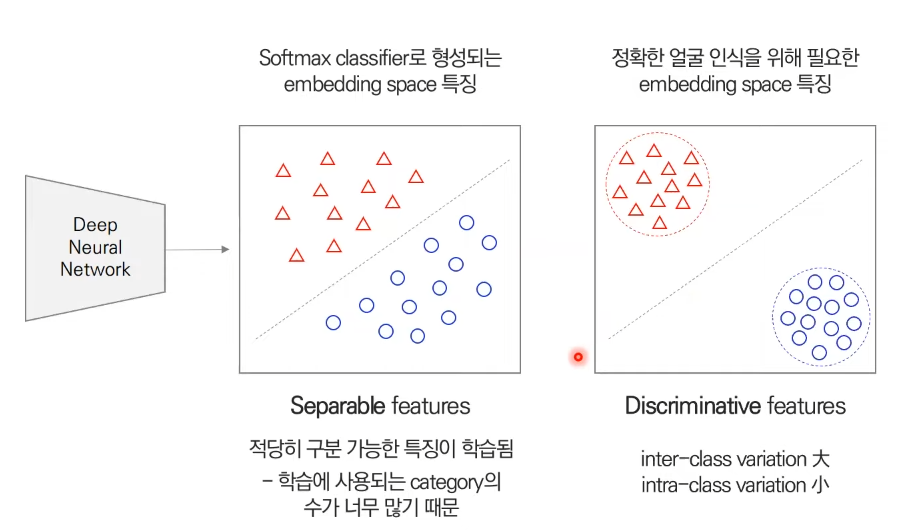
단점 1) 제대로된 특징이 학습되지 않고 얼굴인식 성능이 낮아짐 (inter-class간(빨간 세모와 파란 동그라미)의 분산은 커야되고, intra-class(빨간 세모들)간의 분산은 작아야된다.)
단점 2) 새로운 인물이 들어오면 제대로 된 특징을 학습하지 못함 → 우리가 가진 k개로만 학습이 되었기 때문에

2) Deep Metric Learning 손실함수 종류
- Contrastive loss (2005 CVPR)
- Triplet loss (2015 CVPR)
- Center loss (2016 ECCV)
- Additive angular margin loss (2019 CVPR)

---

[1] Contrastive Loss

• 가장 간단하고 직관적

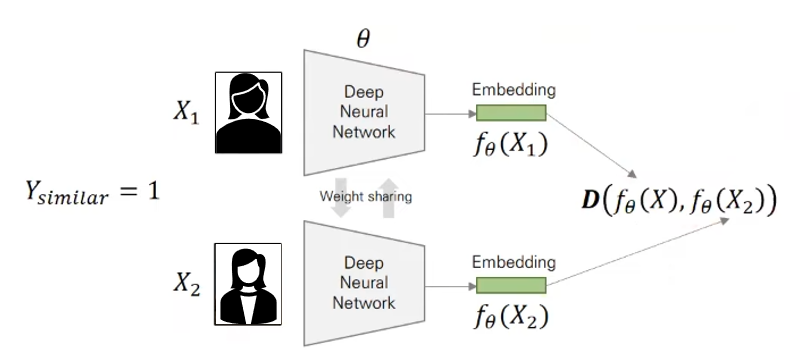
• 두 개의 데이터가 유사하다면 거리가 작아지도록 두 개의 데이터가 유사하지 않다면 거리가 멀어지도록 고안된 손실함수

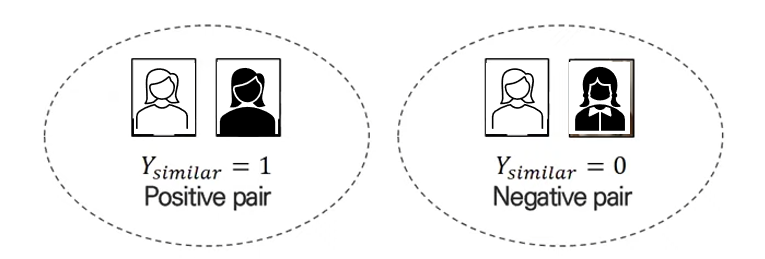
• 두 개의 이미지의 label이 같으면 $Y_{similar}=1$, 다르면 $Y_{similar}=0$

  $L_{contrastive}(\theta, X_1, X_2, Y_{similar})$

  $= Y_{similar}(D^2(f_\theta(X_1), f_\theta(X_2))) + (1-Y_{similar}) max(0, m-D^2(f_\theta(X_1), f_\theta(X_2)))$

• 왼쪽 term : 유사한 이미지가 들어오면 loss를 줄이기 위해 단순히 $Y_{similar}$에 거리(=0) 를 곱해줌
  

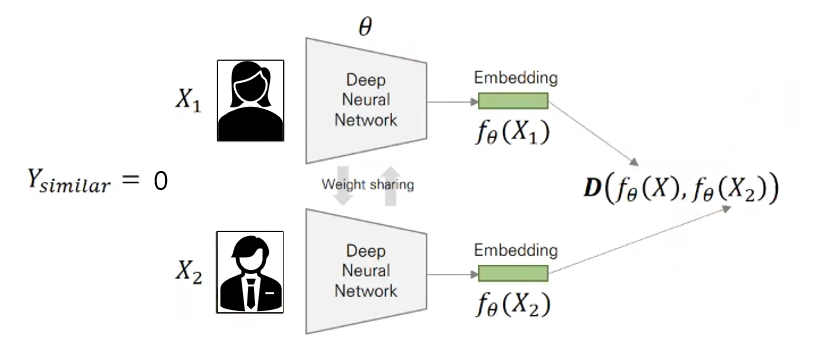
• 오른쪽 term : 유사하지 않은 이미지가 들어오면 $(1-Y_{similar})$은 1이 되고, 뒷부분은 하이퍼파라미터 m을 고려.
  

• 하이퍼파라미터 m
  

• 최종적으로 잠재/임베딩 공간에서 기준이 되는 이미지가 있을 때, 유사한 이미지는 기준이 되는 이미지를 중심으로 margin m 거리 안에 존재하고, 유사하지 않은 이미지는 m보다 멀리 위치한다.

---

[2] Triplet Loss

• 가장 유명하고 널리 활용되는 손실함수
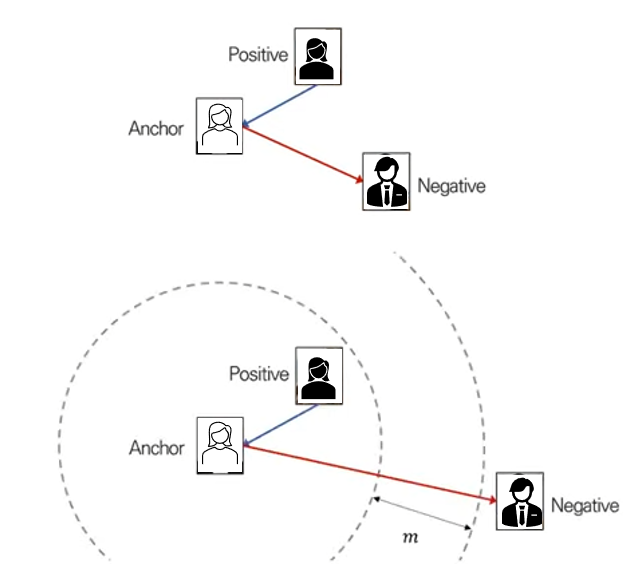
• 세 개의 데이터(anchor, positive, negative) 사용
• positive pair보다 negative pair의 거리가 더 멀어지도록 고안된 손실함수

여기서는 2가지 이미지가 아닌 3가지 이미지를 사용

Anchor(기준이 되는 이미지)에 가까운 이미지를 positive, 유사하지 않은 이미지를 negative로 하여 총 3가지의 이미지를 학습한다.

• positive의 embedding vector = $f_\theta(X_p)$
• anchor의 embedding vector = $f_\theta(X_a)$
• negative의 embedding vector = $f_\theta(X_n)$ 라고 하면

$D(f_\theta(X_a), f_\theta(X_p)) < D(f_\theta(X_a), f_\theta(X_n))$ 여야됨

여기서 확실히 먼 것은 더 멀어지도록 $D(f_\theta(X_a), f_\theta(X_p))$에 m(margin)을 더해준다.

$D(f_\theta(X_a), f_\theta(X_p)) + m < D(f_\theta(X_a), f_\theta(X_n))$
→ $D(f_\theta(X_a), f_\theta(X_p)) + m - D(f_\theta(X_a), f_\theta(X_n)) <0$ (좌변으로 넘김)
→ $L_{triplet}(\theta,X_1,X_2) = max(0, D^2(f_\theta(X_a), f_\theta(X_p)) - D^2(f_\theta(X_a), f_\theta(X_n)) +m)$

위 loss에서 $D^2(f_\theta(X_a), f_\theta(X_p))$(=anchor와 positive 거리)는 줄어드는 방향으로 학습되고, $D^2(f_\theta(X_a), f_\theta(X_n))$(=anchor와 negative 거리)는 앞에 - 부호때문에 증가하는 방향으로 학습이 된다.

---

Contrastive loss, Triplet loss의 경우, 유사한지 유사하지 않은지 = 같은 class에 속하는지 아닌지의 의미이고 결국 class label이 필요하다. 즉, supervised learning인 것이다.

class label이 필요없는 self-supervised learning에서 손실함수로 활용하려면 아래와 같이 pair를 형성해야 된다.

같은 이미지에서 변형된 이미지를 positive pair로 두고, 그렇지 않은 이미지를 negative pair로 둔다.

---

Triplet mining이 성능에 영향을 많이 준다고 한다.

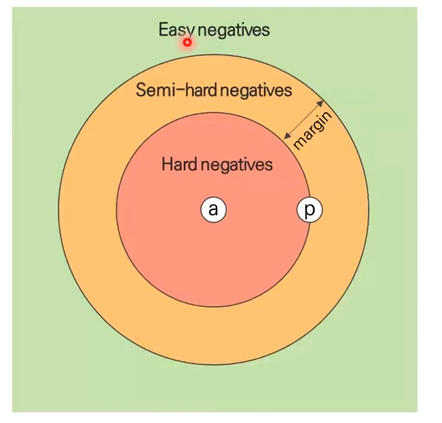
위 그림과 같이 어떤 negative인지에 따라 성능/계산량 차이가 크게 난다. Hard negative도 뽑아서 학습해야지 성능이 높아진다.

---

[3] Center loss
위의 문제를 해결하기 위해서 나온 loss가 center loss이다. class내의 variation은 낮춰주고 class간의 variation의 높여야된다는 idea를 반영하였다.

Softmax(inter-class variation 크게)에 정규식(intra-class variation 작게)을 추가

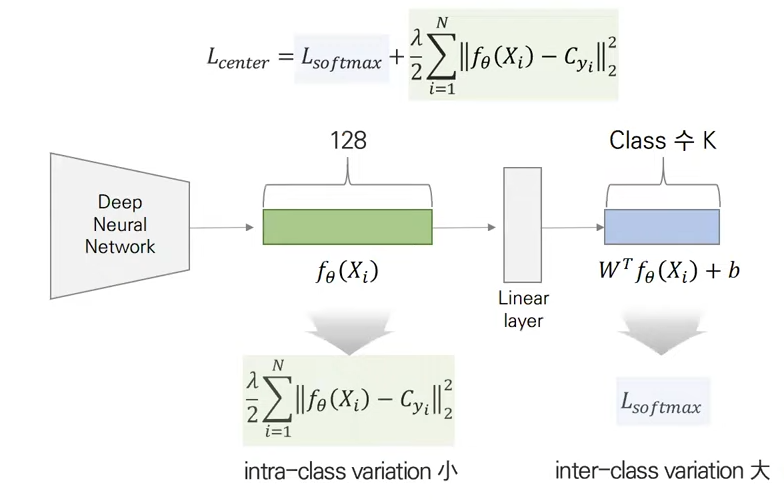
이를 시각화하면 아래와 같다.

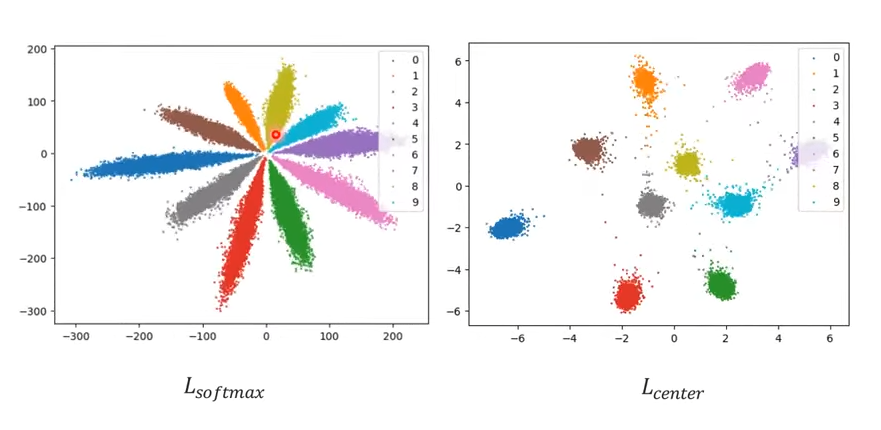
class 내의 variation이 center loss를 사용하였을 때 훨씬 더 작아진 것을 볼 수 있다.

---

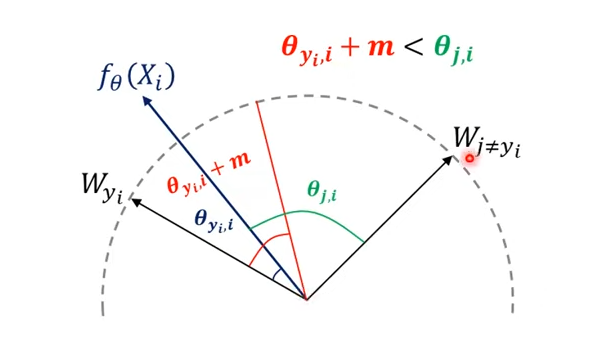
[4] Additive angular margin loss

• softmax 함수를 변형
  

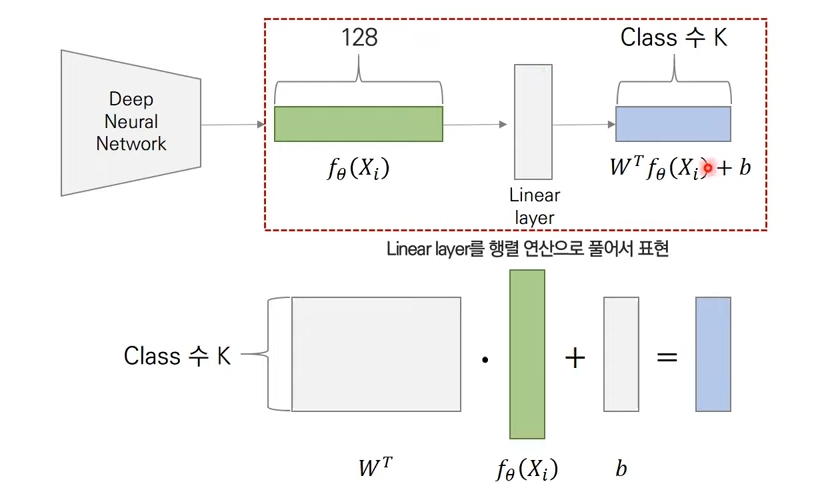
아래과 같이 class 1 대표벡터부터 class 3 대표벡터까지 계산이 되어 최종적인 softmax가 구해진다.

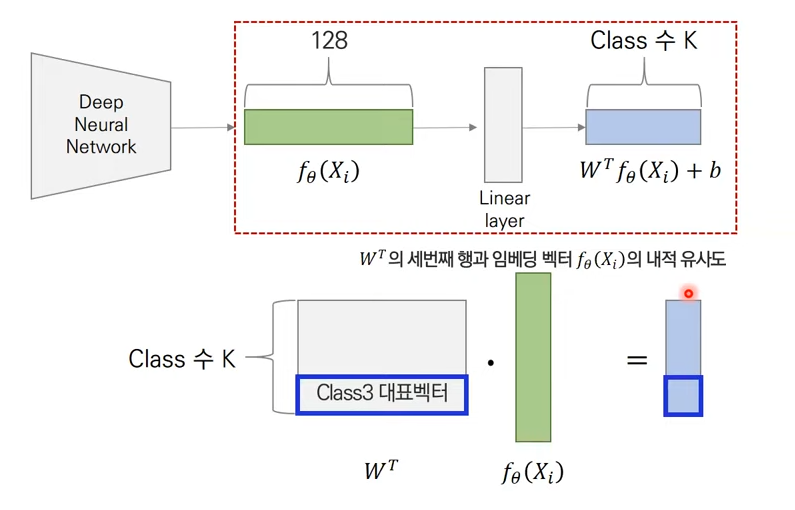
bias가 0이라고 하면, 실제 class 대표 벡터와 들어온 embedding vector의 유사도가 다른 embedding vector와의 유사도에 비해 커질 수 있는 방향으로 해석한다.

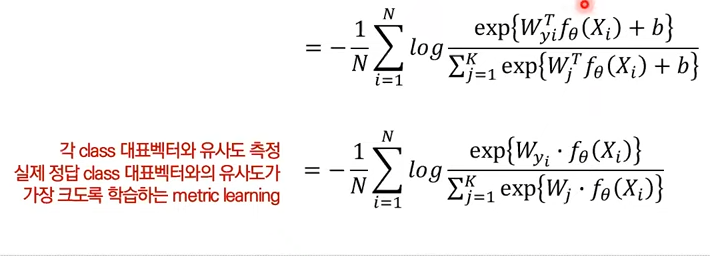
이를 정리하면 아래와 같고 최종적으로는 각도로 embedding vector를 구분하는 것이다.

이렇게 하면 intra class끼리는 작아지고, inter class끼리는 멀어지게 된다.