Big O에 대해서 멋쟁이사자처럼 교육 때 배운 적 있다. 그때는 실습을 더 열심히 해서 그랬는지 이론적인 내용이 잘 기억이 나지 않아서 이번 강의가 알고리즘 개념을 배울 수 있는 좋은 기회인 것 같다. 오늘은 <알고리즘 표기법>이라는 것에 대해서 배우는 시간이었다.
0. 전 시간에 배운 것
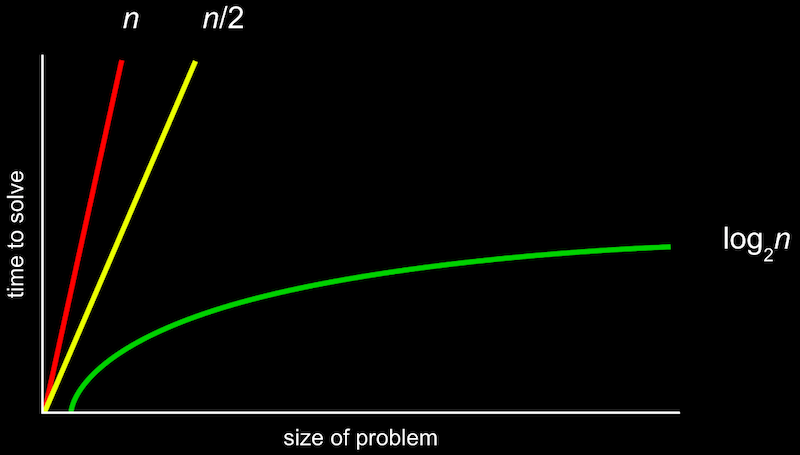
알고리즘은 직선으로 그려지는 선형의 형태이거나 로그 형태일 수 있다. 이 형태는 각 알고리즘이 '최악의 경우(나중에 최상의 경우도 배움)'에 필요한 계산 수를 나타낸다.
여태까지 강의에서 예시로 들었던 전화번호부 페이지 수나 캐비닛의 개수를 n으로 가정한다면, 왼쪽부터 오른쪽까지 n번 확인하여 Mike Smith와 숫자 50을 찾을 수 있다(더 빠른 방법으로 문제를 푼다면 n → n/2처럼 기울기가 줄어든다). 로그함수는 훨씬 더 완만한 형태를 보인다. 로그 너무 오랜만이야...
1. Big O 표기법 👌
컴퓨터 과학자들은 알고리즘을 설명하기 위한 용어를 만든다. 이 용어들은 알고리즘이 얼마나 잘 설계되어 있는지를 말해준다. 가장 대표적으로 Big O 표기법이 있다.
Big O 표기법은 'on the order of'의 약자이다. '대략, ~의 순서로, ~의 방식으로'라는 의미인데, 여기서는 '~만큼 커지면서'라는 의미 정도가 적당한 것 같다.
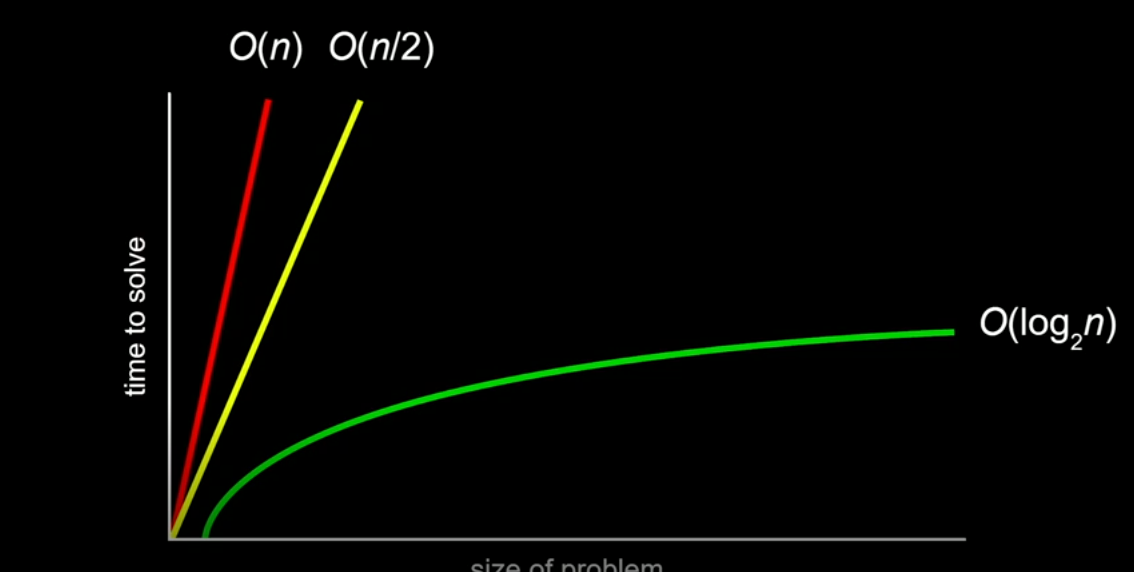
우리가 푸는 문제(size of problem)가 충분히 크다면 O(n), O(n/2)는 비슷하므로 같은 것으로 쳐도 된다. 그래서 컴퓨터 과학자는 알고리즘의 효율성을 설명할 때 정확히는 O(n/2)일지라도 그냥 O(n)이라고 말한다.
예를 들어 알고리즘이 얼마나 효율적인지, 즉 코드의 효율성을 묻는다면 손을 사용해 직관적으로 코드의 속도를 알려줄 수도 있을 거다. 이처럼 n번, n/2번, log n번이라 하지 않고 더 단순하게 표기하기 위해 O(n), O(n/2), O(log n)를 사용한다.
주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용된다.
| Big O notation | 내용 |
|---|---|
| O(n^2) | |
| O(n log n) | |
| O(n) | 선형 검색 |
| O(log n) | 이진 검색 |
| O(1) |
💡 러닝타임(실행 시간): 프로그램이나 알고리즘이 동작하는 데 걸리는 시간을 의미한다.
ex) 몇 초가 걸리는지 혹은 몇 번의 계산 과정이 필요한지
2. Big Ω
Big Ω('빅 오메가'라고 읽음)는 Big O의 반대 표기법이다.
Big O는 알고리즘을 수행하는 데 필요한 시간의 상한선을 의미한다. 즉, 최악의 경우 몇번을 탐색해야 하는지를 나타낸다. 반대로 Omega를 사용하면 최상의 경우를 나타낼 수 있다. 예를 들어 입력값이 특정 순서로 들어온다면 러닝타임이 예상보다 짧아질 수 있다(최상의 경우 한번에 찾을 수도 있다).
그래서 Omega에서는 선형 검색과 이진 검색을 Ω(1)로 표현할 수 있다.
| Big Ω notation | 내용 |
|---|---|
| Ω(n^2) | |
| Ω(n log n) | |
| Ω(n) | 배열 안에 존재하는 값의 개수 세기 |
| Ω(log n) | |
| Ω(1) | 선형 검색, 이진 검색 |
