211116 - 가장 큰 정사각형 찾기

◾ 가장 큰 정사각형 찾기 : 프로그래머스 LEVEL 2

• https://programmers.co.kr/learn/courses/30/lessons/12905

문제

1와 0로 채워진 표(board)가 있습니다. 표 1칸은 1 x 1 의 정사각형으로 이루어져 있습니다. 표에서 1로 이루어진 가장 큰 정사각형을 찾아 넓이를 return 하는 solution 함수를 완성해 주세요. (단, 정사각형이란 축에 평행한 정사각형을 말합니다.)

1	2	3	4
0	1	1	1
1	1	1	1
1	1	1	1
0	0	1	0

가 있다면 가장 큰 정사각형은

1	2	3	4
0	1	1	1
1	1	1	1
1	1	1	1
0	0	1	0

가 되며 넓이는 9가 되므로 9를 반환해 주면 됩니다.

---

입력

• 표(board)는 2차원 배열로 주어집니다.
• 표(board)의 행(row)의 크기 : 1,000 이하의 자연수
• 표(board)의 열(column)의 크기 : 1,000 이하의 자연수
• 표(board)의 값은 1또는 0으로만 이루어져 있습니다.

출력

• 가장 큰 정사각형의 넓이

입출력 예

board	answer
[[0,1,1,1],[1,1,1,1],[1,1,1,1],[0,0,1,0]]	9
[[0,0,1,1],[1,1,1,1]]	4

---

◾ 풀이

1. 해설

• 동적 프로그래밍을 활용하여 해결할 수 있다.
• 현재 위치의 최대 길이는 (왼쪽 위), (왼쪽), (위) 중 최소 길이 + 1로 정의된다.
  
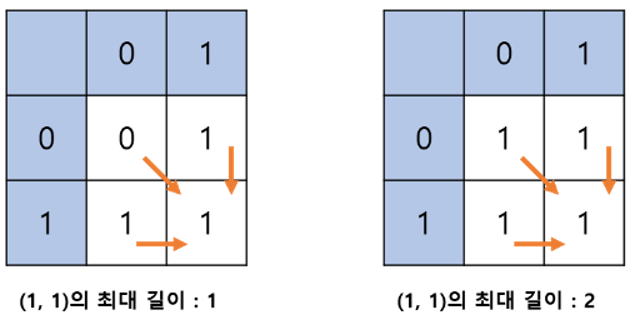
• 가능한 모든 위치에 대해 최대 길이를 계산해나가며 최대값을 선택한다.

---

2. 프로그램

1. 인덱스 시작을 (1, 1)로 하기 위해 new_board 선언
2. new_board의 각 위치의 최대 길이 검사(현재 인덱스 i, j)
3. new_board[i][j] == 1인 경우 최대 길이 검사
4. ([i-1][j-1], [i-1][j], [i][j-1] 중 최소 길이) + 1로 설정
   • answer과 현재 위치의 길이 중 최대값 선택

# 코드
'''
def solution(board):
    answer = board[0][0]    # row 크기    : 1
                            # column 크기 : 1
                            # 위의 경우도 가능하기 때문에 표의 첫 값으로 초기화

    r_len = len(board)      # 표의 행 크기
    c_len = len(board[0])   # 표의 열 크기
    # 인덱스를 [1][1]로 시작하기위해 새로운 행렬 구성
    new_board = [[0] * (c_len+1) for i in range(r_len+1)]
    for idx, r in enumerate(board, start=1):
        new_board[idx][1:] = r
    
    # 행 인덱스: 1, 열 인덱스: 1 부터 가능한 정사각형의 크기 검사
    for i in range(1, r_len+1):
        for j in range(1, c_len+1):
            # 현재 인덱스가 0이 아닌 경우 가능한 최대 크기 검사
            if new_board[i][j] != 0:
                # 현재 인덱스의 (왼쪽 위), (왼쪽), (위) 3개의 값 중 최소값 선택
                # 최소값 + 1을 현재 인덱스에서 가능한 최대 정사각형의 길이로 설정
                new_board[i][j] = min(new_board[i-1][j-1], new_board[i-1][j], new_board[i][j-1]) + 1
                answer = max(answer, new_board[i][j])   # 최대값으로 변경

    return answer ** 2  # 넓이를 구해야하므로 제곱하여 반환