◾ 지형 이동 : 프로그래머스 LEVEL 4
문제
N x N 크기인 정사각 격자 형태의 지형이 있습니다. 각 격자 칸은 1 x 1 크기이며, 숫자가 하나씩 적혀있습니다. 격자 칸에 적힌 숫자는 그 칸의 높이를 나타냅니다.
이 지형의 아무 칸에서나 출발해 모든 칸을 방문하는 탐험을 떠나려 합니다. 칸을 이동할 때는 상, 하, 좌, 우로 한 칸씩 이동할 수 있는데, 현재 칸과 이동하려는 칸의 높이 차가 height 이하여야 합니다. 높이 차가 height 보다 많이 나는 경우에는 사다리를 설치해서 이동할 수 있습니다. 이때, 사다리를 설치하는데 두 격자 칸의 높이차만큼 비용이 듭니다. 따라서, 최대한 적은 비용이 들도록 사다리를 설치해서 모든 칸으로 이동 가능하도록 해야 합니다. 설치할 수 있는 사다리 개수에 제한은 없으며, 설치한 사다리는 철거하지 않습니다.
각 격자칸의 높이가 담긴 2차원 배열 land와 이동 가능한 최대 높이차 height가 매개변수로 주어질 때, 모든 칸을 방문하기 위해 필요한 사다리 설치 비용의 최솟값을 return 하도록 solution 함수를 완성해주세요.
입력
- land는 N x N크기인 2차원 배열입니다.
- land의 최소 크기는 4 x 4, 최대 크기는 300 x 300입니다.
- land의 원소는 각 격자 칸의 높이를 나타냅니다.
- 격자 칸의 높이는 1 이상 10,000 이하인 자연수입니다.
- height는 1 이상 10,000 이하인 자연수입니다.
출력
- 사다리 설치 최소 비용
입출력 예
| land | height | answer |
|---|---|---|
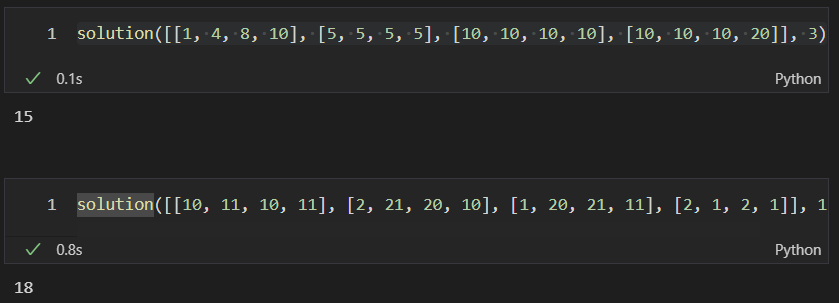
| [[1, 4, 8, 10], [5, 5, 5, 5], [10, 10, 10, 10], [10, 10, 10, 20]] | 3 | 15 |
| [[10, 11, 10, 11], [2, 21, 20, 10], [1, 20, 21, 11], [2, 1, 2, 1]] | 1 | 18 |
◾ 풀이
1. 해설
- 힙을 이용해 이동 비용(설치 비용)이 가장 작은 경로로 이동하며 설치 비용을 구하면 된다.
- [비용, 행 좌표, 열 좌표]
- 최소힙을 이용해 비용 기준으로 작은 곳부터 이동한다.
- BFS(또는 DFS)를 통해 최단 거리를 찾는 일반적인 문제의 변형으로 이동 방향과는 상관없이 설치 비용만 확인하며 진행한다.
2. 프로그램
- n, visit_point, heap_point 초기화
- n : land의 크기
- visit_point : 방문 좌표 표시
- heap_point : 현재 이동 가능한 좌표를 담은 최소힙
- 전체를 방문할 때까지 반복하며 설치 비용이 최소인 구간 확인
- [cost, r, c] : [비용, 행 좌표, 열 좌표]
- 이미 방문한 좌표라면 패스, 방문하지 않은 좌표라면 비용 추가
- 상, 하, 좌, 우 중 이동가능한 좌표 확인
- 높이 차가 height 이하라면 비용은 0, 초과라면 차이만큼의 비용
# 코드
import heapq
def solution(land, height):
answer = 0
n = len(land)
visit_point = [[False] * n for _ in range(n)]
heap_point = [[0, 0, 0]]
while heap_point:
cost, r, c = heapq.heappop(heap_point)
if visit_point[r][c] == True:
continue
visit_point[r][c] = True
answer += cost
for d_r, d_c in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
new_r, new_c = r+d_r, c+d_c
if new_r < 0 or new_r >= n or new_c < 0 or new_c >= n or visit_point[new_r][new_c] == True:
continue
new_cost = abs(land[r][c] - land[new_r][new_c])
if new_cost <= height:
new_cost = 0
heapq.heappush(heap_point, [new_cost, new_r, new_c])
return answer