◾약수와 소수
1. 약수
약수: 어떤 수를 나누어 떨어지게 하는 수- 2 : 1, 2
- 3 : 1, 3
- 8 : 1, 2, 4, 8
# 입력 : 숫자
# 출력 : 입력 숫자의 약수
inputNumber = int(input("0보다 큰 정수 입력 : "))
print('{}의 약수 : '.format(inputNumber), end='')
for number in range(1, inputNumber+1):
# 나머지가 0인 경우 약수 이므로 출력
if inputNumber % number == 0 :
print('{} '.format(number), end=' ')2. 소수
소수: 1과 자기만을 약수로 가지는 수(단, 1은 제외)- 2 : 1, 2
- 3 : 1, 3
- 5 : 1, 5
- 11 : 1, 11
# 입력 : 숫자
# 출력 : 입력 숫자까지의 소수
inputNumber = int(input('0보다 큰 정수 : '))
for number in range(2, (inputNumber + 1)):
flag = True
# 2보다 크고 자신보다 작은 수 중 나누어 떨어지는 수가 있다면
# 소수가 아니므로 flag를 False로 변경한다.
for n in range(2, number):
if number % n == 0:
flag = False
break
if flag:
print('{}\t: 소수!!'.format(number))
else:
print('{}\t: \t합성수!!'.format(number))◾소인수와 소인수분해
- 소인수 : 약수(인수) 중에서 소수인 숫자
- 20의 약수 : 1, 2, 4, 5, 10, 20
- 소인수 : 2, 5
- 36의 약수 : 1, 2, 3, 4, 9, 12, 18, 36
- 소인수 : 2, 3
- 20의 약수 : 1, 2, 4, 5, 10, 20
- 소인수분해 : 1보다 큰 정수를 소인수의 곱으로 나타낸 것
- 20의 소인수 분해 : 2 X 10
- 10의 소인수 분해 : 2 X 5
- 20 = 2 X 2 X 5 = 2^2 X 5
- 소인수분해와 약수 : 소인수 분해를 통해 약수를 정확하고 쉽게 찾을 수 있다.
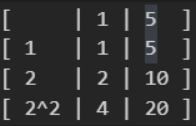
- 20의 소인수 분해 : 2^2 X 5
- 행(1, 2, 2^2), 열(1, 5)와 같이 행렬로 표현 가능
# 입력 : 정수
# 출력 : 소인수분해
inputNumber = int(input('1보다 큰 정수 : '))
n = 2
while n <= inputNumber:
# 소인수만을 출력한다.
if inputNumber % n == 0:
print('소인수 : {}'.format(n))
inputNumber /= n
# 소인수가 아니라면 n을 1 증가시킨다.
else:
n += 1◾최대공약수, 최소공배수
1. 최대공약수
공약수: 두 개 이상의 수에서 공통된 약수- 12의 약수 : 1, 2, 3, 4, 6, 12
- 20의 약수 : 1, 2, 4, 5, 10, 20
- 공약수 : 1, 2, 4
최대공약수: 공약수 중 가장 큰 수- 12와 20의 최대공약수 : 4
- 소인수분해를 이용하여 최대공약수 및 공약수를 구할 수 있다.
- 공통된 소인수의 거듭제곱에서 지수가 작은 수를 모두 곱한다.
- 12의 소인수분해 : 2^2 * 3
- 20의 소인수분해 : 2^2 * 5
- 최대공약수 : 2^2 = 4
- 공약수 : 4의 약수 => 1, 2, 4
- 소수로 나눗셈을 진행하는 방법도 있다.
- (12 20) / 2 = (6 10)
- (6 10) / 2 = (3 5)
- (3 5) => 2 * 2 =4
- 일반적인 방법
# 입력 : 두 수
# 출력 : 최대공약수
num1 = int(input('1보다 큰 정수 : '))
num2 = int(input('1보다 큰 정수 : '))
maxNum = 0
for i in range(1, (num1 + 1)):
# 두 수 모두 나누어 떨어뜨리는 수만 출력
if num1 % i == 0 and num2 % i ==0:
print('공약수 : {}'.format(i))
# 값을 증가시키며 비교하기 때문에
# 새로운 공약수가 최대공약수가 된다.
maxNum = i
print('최대 공약수 : {}'.format(maxNum))- 유클리드 호제법 : x, y의 최대공약수는 y, r(x%y)의 최대공약수와 같다.
- 12 % 36 = 12
- 36 % 12 = 0
- 12와 36의 최대공약수 : 12
- 12 % 20 = 12
- 20 % 12 = 8
- 12 % 8 = 4
- 8 % 4 = 0
- 12와 20의 최대공약수 : 4
# 입력 : 두 수
# 출력 : 최대공약수
num1 = int(input('1보다 큰 정수 : '))
num2 = int(input('1보다 큰 정수 : '))
# temp1 : x, temp2 : y
temp1 = num1; temp2 = num2
# 유클리드 호제법 사용
while temp2 > 0:
temp = temp2
temp2 = temp1 % temp2
temp1 = temp
print("{}, {}의 최대공약수 : {}".format(num1, num2, temp1))
# 두 수의 공약수는 최대고약수의 공약수와 같다.
for n in range(1, temp1+1):
if temp1 % n == 0:
print('{}, {}의 공약수 : {}'.format(num1, num2, n))2. 최소공배수
공배수: 두 개 이상의 수에서 공통된 배수최소공배수: 공배수 중 가장 작은 수- 3의 배수 : 3, 6, 9, 12, 15...
- 5의 배수 : 5, 10, 15, 20, 25...
- 공배수 : 15, 30...
- 최소공배수 : 15
- 최소공배수 구하기
- 소인수분해를 이용해 최소공배수 및 공배수를 구할 수 있다.
- 공통인 소인수의 거듭제곱에서 지수가 ㅋ고 공통아닌 수를 모두 곱한다.
- 4의 소인수분해 : 2^2
- 12의 소인수분해 : 2^2 * 3
- 최소공배수 : 2^2 * 3 = 12
- 공배수 : 12의 배수
- 좀 더 편리하게 구하는 방법
- 소수로 나눗셈하여 구할 수 있다.
- (6 12) % 2 = (3 6)
- (3 6) % 3 = (1 2)
- (1 2)
- 2 3 1 2 = 2^2 3 = 12
- 소수로 나눗셈하여 구할 수 있다.
# 입력 : 두 수
# 출력 : 최소공배수
num1 = int(input('1보다 큰 정수 : '))
num2 = int(input('1보다 큰 정수 : '))
maxNum = 0
for i in range(1, (num1 + 1)):
if ship1 % i == 0 and num2 % i ==0:
print('공약수 : {}'.format(i))
maxNum = i
print('최대 공약수 : {}'.format(maxNum))
# 최소공배수
# 두 수를 곱하여 최대공약수로 나누면 최소공배수가 된다.
minNum = (num1 * num2) // maxNum
print('최소공배수 : {}'.format(minNum))◾진법
- 진법 : 특정 숫자 몇 개를 사용하여 수를 표시하는 방법
2진법: 0과 1로 표현8진법: 0 ~ 8로 표현10진법: 0 ~ 9로 표현16진법: 0 ~ 9, A ~ F 로 표현
- 10진수 X진수 변환
- 2진수 변환 : 더이상 나눌 수 없을 때까지 2로 나누고 각 수를 묶어 표현한다.
- 8 / 2 = 4..0
- 4 / 2 = 2..0
- 2 / 2 = 1..0
- 2진수 : 1000
- 8진수 변환 : 더이상 나눌 수 없을 때까지 8로 나누고 각 수를 묶어 표현한다.
- 25 / 8 = 3..1
- 8진수 : 31
- 16진수 변환 : 더이상 나눌 수 없을 때까지 16으로 나누고 각 수를 묶어 표현한다.
- 25 / 16 = 1..9
- 16진수 : 19
- 2진수 변환 : 더이상 나눌 수 없을 때까지 2로 나누고 각 수를 묶어 표현한다.
- X진수 10진수 변환
- 2진수 변환 : 자리수가 n 이라면 각 자리수에 2^n-1 ~ 2^0을 차례로 곱하여 더해준다.
- 1000 = 1 2^3 + 0 2^2 + 0 2^1 + 0 2^0 = 8
- 8진수 변환 : 자리수가 n 이라면 각 자리수에 8^n-1 ~ 8^0을 차례로 곱하여 더해준다.
- 31 = 3 8^1 + 1 8^0 = 25
- 16진수 변환 : 자리수가 n 이라면 각 자리수에 16^n-1 ~ 16^0을 차례로 곱하여 더해준다.
- 19 = 1 16^1 + 9 16^0 = 25
- 2진수 변환 : 자리수가 n 이라면 각 자리수에 2^n-1 ~ 2^0을 차례로 곱하여 더해준다.
- 2진수 -> 8진수 변환
- 뒤에서 부터 3자리씩 구분하고 빈 자리는 0으로 채운다
- 각 자리수에 2^2 ~ 2^0을 곱하여 더한다.
- 2진수 : 1010100
- 001 | 010 | 100 = 124
- 0(2^2) + 0(2^1) + 1*(2^0) = 1
- 0(2^2) + 1(2^1) + 0*(2^0) = 2
- 1(2^2) + 0(2^1) + 0*(2^0) = 4
- 2진수 ->16진수 변환
- 뒤에서 부터 4자리씩 구분하고 빈 자리는 0으로 채운다
- 각 자리수에 2^3 ~ 2^0을 곱하여 더한다.
- 2진수 : 1010100
- 0101 | 0100 = 54
- 0(2^3) + 1(2^2) + 0(2^1) + 1(2^0) = 5
- 0(2^3) + 1(2^2) + 0(2^1) + 0(2^0) = 4
# 10진수 X진수 변환
# binary : bin() - 0b숫자로 표현
# octal : oct() - 0o숫자로 표현
# Hexadecimal : hex() - 0x숫자로 표현
dNum = 150
print('2진수 : {}'.format(bin(dNum)))
print('8진수 : {}'.format(oct(dNum)))
print('16진수 : {}'.format(hex(dNum)))
# 변환 결과는 문자열
print('Type of bin(dNum) : {}'.format(type(bin(dNum))))
print('Type of oct(dNum) : {}'.format(type(oct(dNum))))
print('Type of hex(dNum) : {}'.format(type(hex(dNum))))
# format 함수 활용 : #생략도 가능
print('2진수 : {}'.format(format(dNum,'#b')))
print('8진수 : {}'.format(format(dNum,'#o')))
print('16진수 : {}'.format(format(dNum, '#x')))
# format 활용
print('{0:#b}\t{1:#o}\t{2:#x}'.format(dNum, dNum, dNum))
# X진수 10진수 변환
# int형변환
print('2진수(0b11110) -> 10진수({})'.format(int('0b11110', 2)))
print('8진수(0o36) -> 10진수({})'.format(int('0o36',8)))
print('16진수(0x1e) -> 10진수({})'.format(int('0x1e', 16)))
# X진수 X진수 변환
# bin, oct, hex, int 활용
print('2진수(0b11110) -> 8진수({})'.format(oct(0b11110)))
print('8진수(0o36) -> 16진수({})'.format(hex(0o36)))
print('8진수(0o36) -> 10진수({})'.format(int(0o36)))
후라이드 치킨