알고리즘 - 그래프 심화(1)

✔ 서로소 집합(Disjoint-Set / Union Find)

• 서로소 혹은 상호 배타 집합
  • 서로 중복으로 포함하는 원소(공통 원소)가 없는 집합
  • 집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분하고 이를 대표자(representative)라고 함

◾서로소 집합을 표현하는 방법

• 집합 구성 요소(원소) 표현
  • 연결 리스트
  • 트리

◾서로소 집합 연산

• Make-Set(x): 집합 생성(x를 원소로 갖는 집합)
  • x만 속한 집합이기 때문에 x가 대표자가 됨
• Find-Set(x): x가 속한 집합을 찾는 것
  • x가 속한 집합의 대표자를 return
• Union(x, y): x와 y 원소를 하나의 집합으로 만들기
  • 우선 두 원소가 포함된 집합이 서로소 집합인지(대표자가 다른지) 확인 필요
  • 서로소 집합이 아닌 경우(대표자가 같은 경우) union 할 수 없음.
    • 이미 같은 집합임을 의미.
  • 내부적으로 find-set을 호출해서 대표자를 비교.

◾서로소 집합 예

• 원소 크기가 1인 배열은 이미 정렬되어 있다는 특징이 있음
• 서로 다른 원소를 가진, 크기가 1인 집합은 이미 서로소 집합임

1. 서로소 집합 표현 : 연결 리스트

• 같은 집합의 원소들은 하나의 연결 리스트로 관리.
• 연결 리스트의 맨 앞 원소 : 집합의 대표 원소
  • 각 원소는 집합의 대표 원소를 가리키는 링크를 가짐
  • 두 개의 link pointer를 가짐 (tail : 다음 원소, rep: 대표자)
  • 두 개의 집합 A, B를 Union 시 B의 대표자를 A의 tail에 연결하고, B 원소들의 대표자 링크 포인터에 A의 대표자를 할당

2. 서로소 집합 표현 : 트리

• 같은 집합의 원소들을 하나의 트리로 표현 : 자식 노드가 부모 노드를 가리킴.
• 트리의 루트 노드 : 집합의 대표 원소
  • 두 개의 집합을 Union 시 대표자끼리 합쳐야 집합이 온전하게 합쳐짐
    • 집합을 합치기 위해.
  • 트리 형태의 서로소 집합은 부모를 거듭해서 루트까지 찾아가야 대표자를 찾을 수 있음 → <재귀>
• 서로소 집합을 표현한 트리의 배열을 이용한 저장된 모습 예시 : 부모 인덱스가 자기 자신인 경우 루트 노드.
  

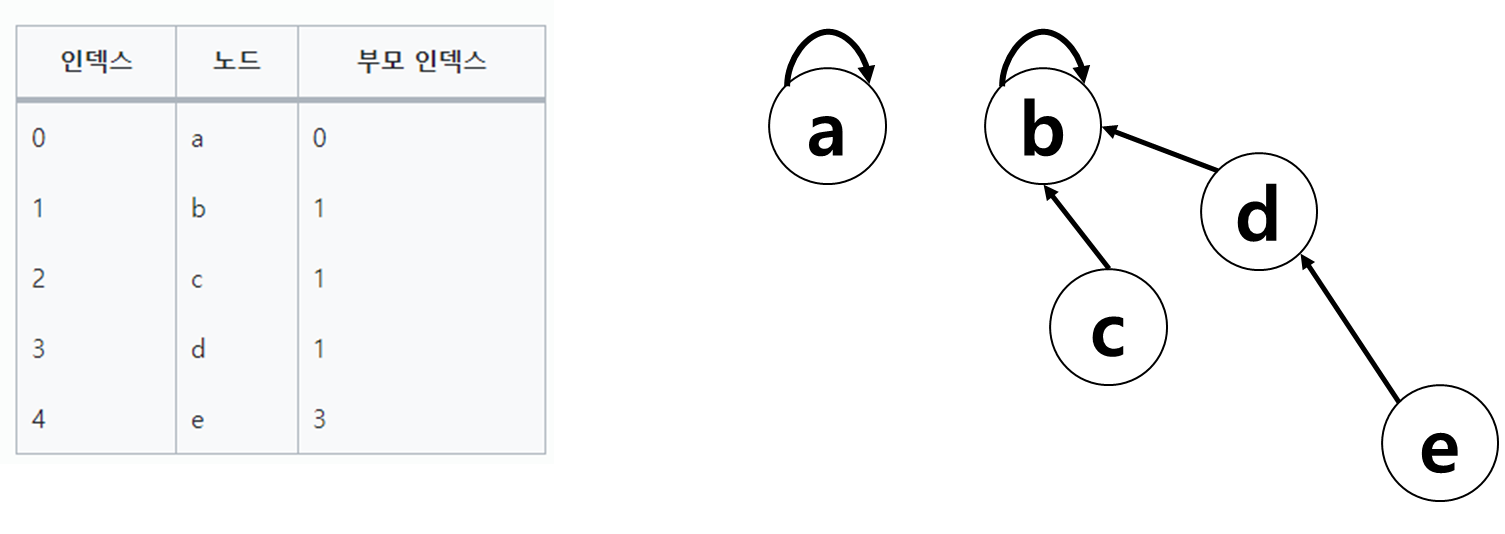
◾서로소 집합에 대한 연산.

• Make-Set(x) : 유일한 멤버 x를 포함하는 새로운 집합 생성.

Make-Set(x){
	p[x] = x;
}

• Find_Set(x) : x를 포함하는 집합을 찾는 연산.

Find-Set(x){
	if (x == p[x]) return x;
    else return Find-Set(p[x]);
}

• Union(x, y) : x와 y를 포함하는 두 짛바을 통합하는 연산.

Union(x){
	// 만약 동일 집합이라면 종료.
	if (Find-Set(x) == Find-Set(y)) return;
    p[Find-Set(y)] = Find-Set(x);
}

• 문제점 : Union 연산 진행 순서에 따라 편향된 트리가 될 수 있음.
  • Rank를 이용한 Union
    • 각 노드는 자신을 루트로 하는 subtree의 높이 rank로 저장.
    • 두 집합을 합칠 때 rank가 낮은 집합을 rank가 높은 집합에 연결.
  • Path Compression
    • Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 root를 가리키도록 포인터를 갱신.

◾Path Compression

• Find-Set 함수를 수정하여 간단하게 Path Compression을 구현할 수 있음.

Find-Set(x){
	if (x == p[x]) return x;
    // p[x]를 갱신하는 코드 추가.
    else return p[x] = Find-Set(p[x]);
}

---

✔ 최소 신장 트리(MST)

• 그래프에서 최소 비용 문제
  • 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리.
  • 두 정점 사이의 최소 비용의 경로 찾기.
• 신장 트리 : n 개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리.
  • 모든 정점이 다른 정점들과의 유일한 경로가 존재함을 보이기 위해 사용.
  • 간선에 방향성이 있는 경우 모든 정점을 탐색할 수 있는 경로가 만들어지지 않을 수 있으므로 무향 그래프에서만 사용.
• 최소 신장 트리(Minimum Spanning Tree) : 무향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리.

---

✔ Kruskal 알고리즘

• 간선을 하나씩 선택해 MST를 찾는 알고리즘 : 시간 복잡도 O(ElogE).
  1. 최초, 모든 간선을 가중치에 따라 오름차순 정렬.
  2. 가중치가 가장 낮은 간선부터 선택하며 트리 증가.
     • 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택.
  3. n-1개의 간선이 선택될 때까지 2 반복

// Union Find를 적용해 Kruskal 알고리즘 구현.
// G.V : 그래프의 정점 집합.
// G.E : 그래프의 간선 집합.

MST-KRUSKAL(G, w){
	for (vertex v : G.v){
    	Make-Set(v);
    }
    
    // G.E에 포함된 간선 가중치 w를 이용한 오름차순 정렬.
    
    for (edge e : G.E){
    	// 싸이클 체크.
    	IF(Find-Set(u) != Find-Set(v){
        	Union(u, v);
        }
    }
    
}

---

✔ Prim 알고리즘

• 정점을 하나씩 선택하며 MST를 찾는 알고리즘 : 시간 복잡도 O(VlogV + ElogV), 최소힙을 사용하지 않는 경우 O(V^2).
  1. 임의 정점 하나 선택하여 시작.
  2. 선택한 정점과 인접한 정점들 중 최소 비용의 간선이 존재하는 정점 선택.
     • 사이클이 존재하면 다음으로 가중치가 낮은 간선이 존재하는 정점 선택.
  3. n개의 정점이 선택될 때까지 2 반복
• 서로소인 2개의 집합(2 disjoint-sets) 정보 유지.
  • 트리 정점들(Tree Vertices) : MST를 만들기 위해 선택된 정점들.
  • 비트리 정점들(non-tree vertices) : 선택되지 않은 정점들.

// Prim 알고리즘 구현.
// G : 그래프
// r : 시작 정점
// minEdge[] : 각 정점 기준 타 정점과의 최소 간선 비용
// G.V : 그래프의 정점 집합.
// G.E : 그래프의 간선 집합.

MST-PRIM(G, r){
	result = 0, cnt = 0;
    for (vertex u : G.V){
    	minEdge[u] = INF;
    }
    minEdge[r] = 0;
    
    While (true){
    	u = Extract-Min()	// 방문하지 않은 최소 비용 정점 찾기.
        visited[u] = true;
        result = result + minEdge[u];
        if(++cnt == N) break;
        for(Vertex v : G.Adj[u]){
        	// u -> v 비용이 v의 최소 비용보다 작다면 갱신.
        	if(visited[v] == false && w(u, v) < minEdge[v]{
            	minEdge[v] = w(u, v)
            }
        }
    }
    
    return result
}