알고리즘 - 분할 정복

✔분할 정복(Divide and Conquer)

• 유래

  • 전력이 우세한 연합군을 공격하기 위해 나폴레옹은 연합군의 중앙부로 쳐들어가 연합군을 둘로 나눔.
  • 둘로 나뉜 연합군을 한 부분씩 격파.

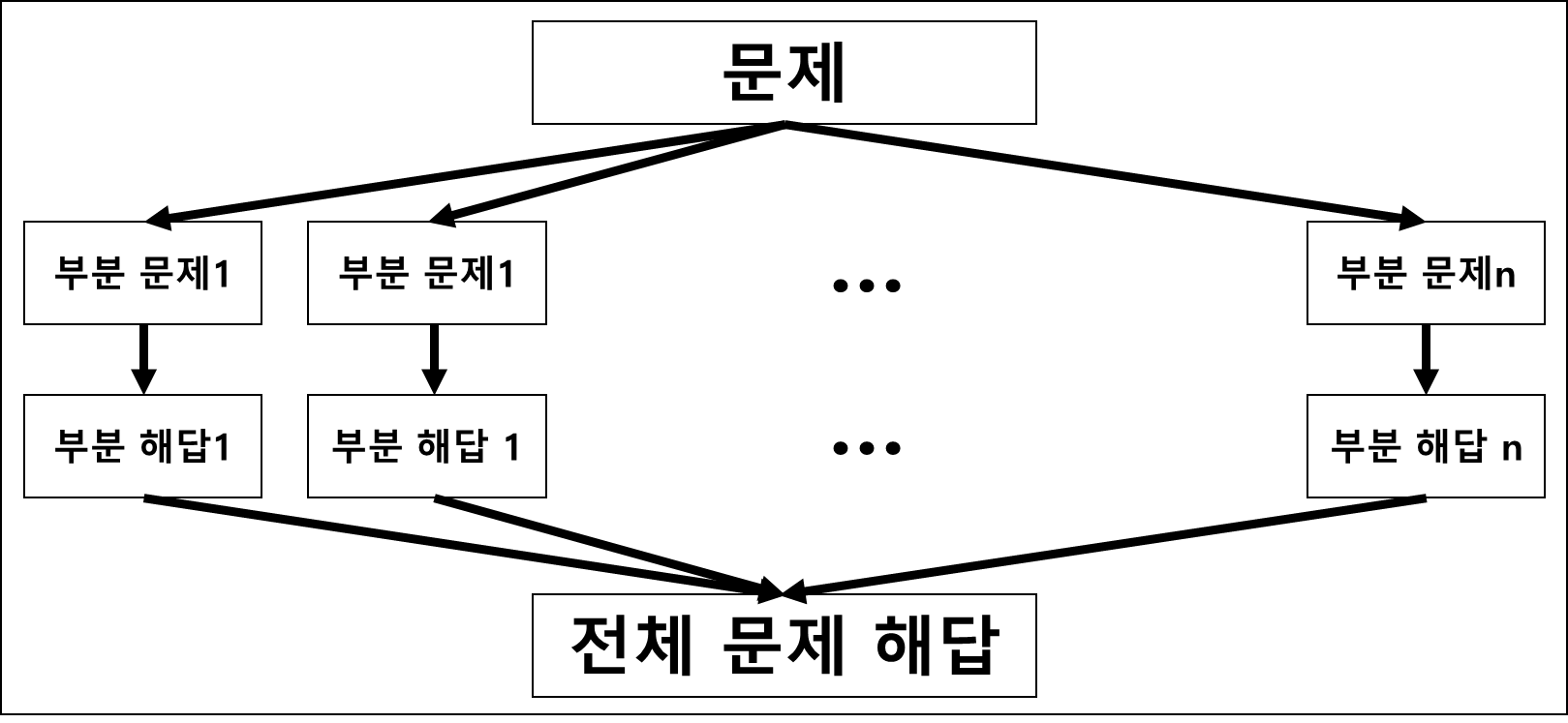
• 설계 전략

  • 분할(Divide) : 해결할 문제를 여러 개의 작은 부분으로 나눔.
  • 정복(Conquer) : 나눈 작은 문제를 각각 해결.
  • 통합(Combine) : (필요하다면) 해결된 답 모음.

• Top-Down Approach
  

1. 거듭 제곱

• 반복(Iterative) 알고리즘 : O(n)
  • Cn = C X C X C X ... X C
• 분할 정복 기반의 알고리즘 : O(logN)
  • Cn = $\begin{cases} C^{n/2} \times C^{n/2} (n은 짝수)\\ C^{(n-1)/2} \times C^{(n-1)/2} \times C (n은 홀수) \end{cases}$

// 분할 정복 거듭 제곱
Recursive_power(T x, int n){
	if (n == 1) return x;
    if (n % 2 == 0){
    	T y = Recursive_power(x, n/2);
        return y * y
    }else{
    	T y = Recursive_power(x, (n-1)/2);
        return y * y * x
    }
}

2. 이진 검색(Binary Search)

• 자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색 진행.
  • 필수 : 정렬된 자료
  • 시간 복잡도 : O(logN) (순차 탐색 : O(N))
• 검색 과정 (자료는 오름차순 정렬되어 있다고 가정.)
  1. 자료의 중앙에 있는 원소 선택.
  2. 중앙 원소 값과 목표 값 비교.
  3. 일치하면 탐색 종료.
  4. 중앙 원소 값이 작을 경우 오른쪽 반에 대해서 새로 검색 수행. 중앙 원소 값이 큰 경우 왼쪽 반에 대해서 새로 검색 수행.
  5. 목표 값을 찾을 때까지 반복.

// 반복을 통한 이진 검색
int binaerySearch(S[], n, key){
	start = 0;
    end = n-1;
    
    while (start <= end){
    	mid = (start+end) / 2;
        if(S[mid] == key){
        	return mid;
        }else if(S[mid] < key){
        	start = mid + 1;
        }else if(S[mid] > key){
        	end = mid - 1;
        }
    }
    return -1;
}

// 재귀를 통한 이진 검색
int binaerySearch(S[], start, end, key){
	if (start > end)
    	return -1;
    else{
    	mid = (start + end) / 2;
        if(S[mid] == key){
        	return mid;
        }else if(S[mid] < key){
        	return binarySearch(S[], mid+1, end, key);
        }else if(S[mid] > key){
        	return binarySearch(S[], start, mid-1, key);
        }
    }
}

• java.util.Arrays.binarySearch : 이진탐색 API
  • 필수 : 정렬된 배열 전달
  • int binarySearch(T[] a, T key)
  • int binarySearch(T[] a, int fromIndex, int toIndex, T key)
  • 결과 반환
    • 원소를 찾을 경우 : [찾은 원소의 Index] 반환.
    • 원소를 못찾을 경우 : [-(있어야하는 Index) - 1] 반환.