알고리즘 - 재귀 알고리즘

◾재귀 알고리즘

• 재귀 알고리즘 : 자신을 다시 호출하는 것
  • 재귀 종료 조건을 준비하지 않으면 무한 루프가 발생한다.
  • 아래 예시에서는 num <= 0일 경우 종료되는 조건을 추가해주었다.

# 재귀 알고리즘
def recursion(num):
    if num > 0 :
        print('*'*num)
        return recursion(num-1)
    else:
        return 1

---

◾하노이 탑

• 하노이 탑 : 퍼즐 게임의 일종으로 세 개의 기둥을 이용해 원판을 다른 기둥으로 옮긴다.
  • 한 번에 한 개의 원판만 옮길 수 있다.
  • 큰 원판이 작은 원판 위에 있어서는 안된다.

# 하노이 탑 이동 순서 출력
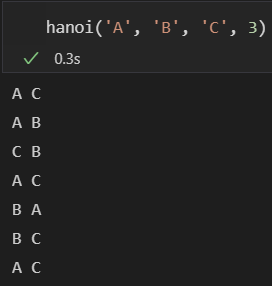
def hanoi(start, to, end, n):
    if n == 1:
        print(start, end)
    else:
        hanoi(start, end, to, n-1)
        print(start, end)
        hanoi(to, start, end, n-1)

---

◾정렬

1. 합병 정렬

• 병합 정렬 : 자료구조를 분할하고 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬
  • [8, 1, 4, 3, 2, 5, 10, 6]
  • [8, 1, 4, 3][2, 5, 10, 6]
  • [8, 1][4, 3] [2, 5][10, 6]
  • [8, 1][4, 3] [2, 5][10, 6]
  • [8][1] [4][3] [2][5] [10][6]
  • [1, 8][3, 4] [2, 5][6, 10]
  • [1, 3, 4, 8][2, 5, 6, 10]
  • [1, 2, 3, 4, 5, 6, 8, 10]

# 병합 정렬
def mSort(ns):
    if len(ns) < 2:
        return ns
    midIdx = len(ns) // 2
    leftNums = mSort(ns[:midIdx])
    rightNums = mSort(ns[midIdx:])

    mergeNums = []
    leftIdx = 0; rightIdx = 0

    while leftIdx < len(leftNums) and rightIdx < len(rightNums):
        if leftNums[leftIdx] < rightNums[rightIdx]:
            mergeNums.append(leftNums[leftIdx])
            leftIdx += 1
        else:
            mergeNums.append(rightNums[rightIdx])
            rightIdx += 1
    
    mergeNums = mergeNums + leftNums[leftIdx:]
    mergeNums = mergeNums + rightNums[rightIdx:]

    return mergeNums

nums = [8, 1, 4, 3 ,2, 5, 10, 6]
print('mSort(nums) : {}'.format(mSort(nums)))

2. 퀵 정렬

• 퀵 정렬 : 기준 값보다 작은 값과 큰 값으로 분리한 후 다시 합친다.
  • [8, 1, 4, 3, 2, 5, 10, 6]
  • [1, 4, 3, 2, 4] | [5] | [8, 10, 6, 8]
  • [1, 2] | [3] | [4, 4] | [5] | [6] | [8, 8, 10]
  • [1] | [2] | [3] | [4] | [4] | [5] | [6] | [8] | [8][10]

# 퀵 정렬
def qSort(ns):
    if len(ns) < 2 :
        return ns

    midIdx = len(ns) // 2
    midVal = ns[midIdx]

    smallNums = []
    sameNums = []
    bigNums = []

    for n in ns:
        if n < midVal:
            smallNums.append(n)
        elif n == midVal:
            sameNums.append(n)
        else:
            bigNums.append(n)
        
    return qSort(smallNums) + sameNums + qSort(bigNums)

nums = [8, 1, 4, 3, 2, 5, 10, 6]
print('not sorted nums : {}'.format(nums))
print('sorted nums : {}'.format(qSort(nums)))