알고리즘 - 힙

✔ 힙

• 힙(Heap) : 완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해 만든 자료구조
  • 각 힙의 조건은 트리의 모든 노드에 적용

◾최대 힙(Max Heap)

• 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
• 부모 노드의 키 값 >= 자식 노드의 키 값
• 루트 노드 : 키 값이 가장 큰 노드

◾최소 힙(Min Heap)

• 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
• 부모 노드의 키 값 <= 자식 노드의 키 값
• 루트 노드 : 키 값이 가장 작은 노드

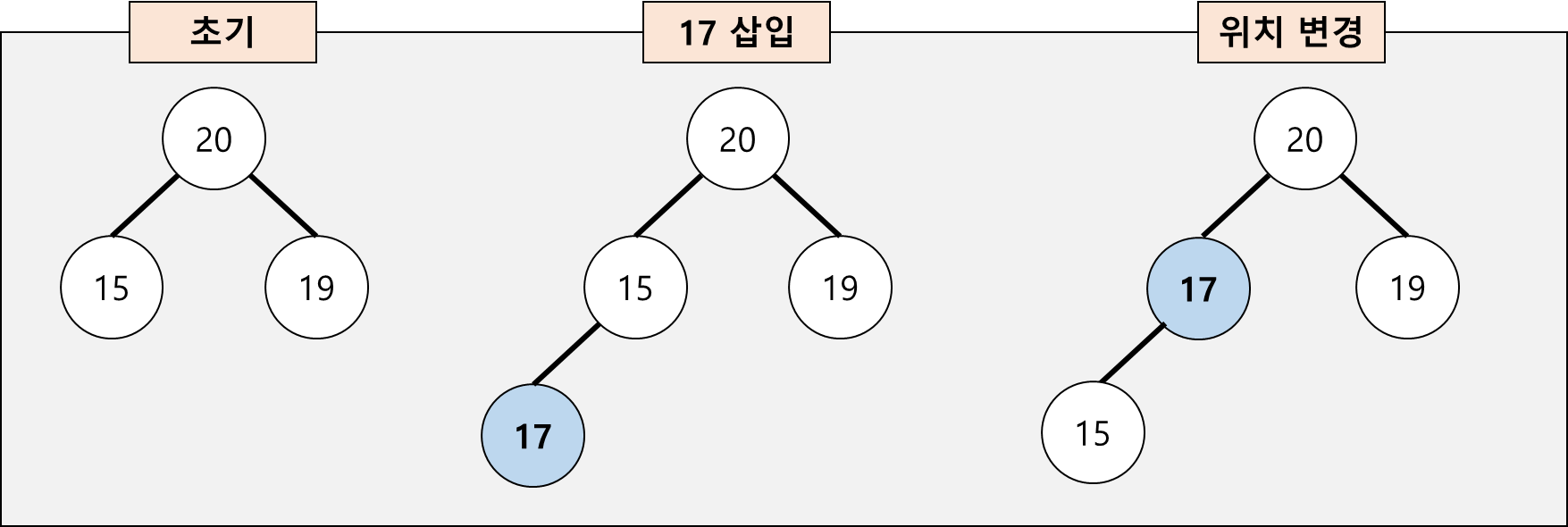
◾힙 연산 - 삽입

• 시간 복잡도 : O(logN)
• 필수 : 완전 이진 트리 조건 유지
  1. 마지막 인덱스 뒤에 추가
  2. 부모와 비교를 통해 위치 변경.

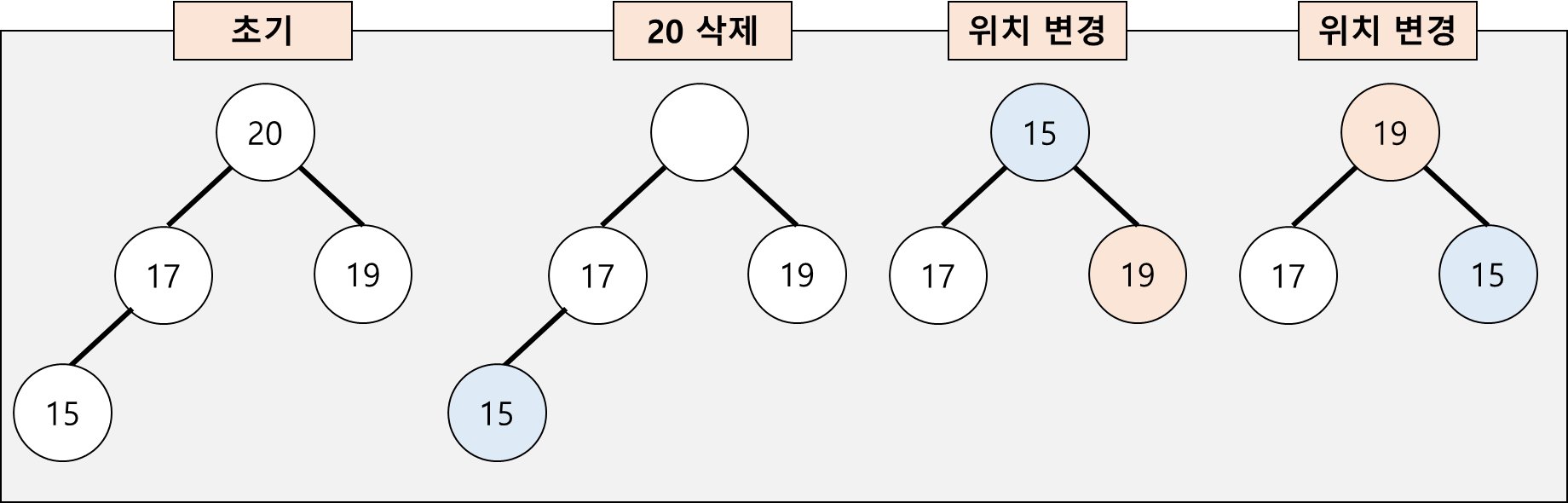
◾힙 연산 - 삭제

• 시간 복잡도 : O(logN)
• 필수 : 완전 이진 트리 조건 유지
  1. 루트 삭제. (힙에서는 루트 노드의 원소만 삭제 가능)
  2. 마지막 인덱스의 값 루트로 이동.
  3. 자식과 비교를 통해 위치 변경.

◾우선순위 큐

• 우선순위 큐(Priority Queue) : 우선순위를 가진 항목들을 저장하는 큐.
  • FIFO가 아닌 우선순위가 높은 순서대로 출력.
    • 원소 비교를 위해 Comparable 구현.
    • 또는 Comparator를 사용해 비교 기준 제공.
  • 노드 하나의 추가/삭제 시간 복잡도 O(logN)
  • 최대값/최소값 O(1)
  • 완전 정렬보다 관리 비용이 적음.
• 배열을 통해 트리 형태 쉽게 구현
  • 부모나 자식 노드 접근 O(1)
  • n위치에 있는 노드의 자식은 2n, 2n+1
  • 완전 이진 트리의 특성에 의해 추가/삭제의 위치는 자료의 시작과 끝 인덱스로 판단 가능.
• java.util.PriorityQueue
  • Heap 자료구조
  • 최대 Heap : 가장 큰 값을 기준으로 출력.
  • 최소 Heap : 가장 작은 값을 기준으로 출력.