정말 잘 정리해주신 "Diffusion Model 수학이 포함된 tutorial" 을 보며 정리한 내용입니다.

Diffusion Model : 이미지에 단계적으로 노이즈를 추가하고, 이를 학습된 신경망으로 노이즈를 제거

1. DDPM

---

Forward Process

• 매우 작은 영역에서의 지속적인 가우시안 커널을 통과하는 과정
• $\beta_t$를 통해 전의 이미지 값인 $\mathbf{x_{t-1}}$을 감소시키면서 $\beta_t$만큼의 노이즈를 조금 더함
  - $\beta_t$ : step size (매우 작은 값) (사전에 정하는 하이퍼 파라미터)
• 아래와 같이 최종적으로 가우시안 분포를 갖는 이미지가 될 때까지 더하는 과정
  

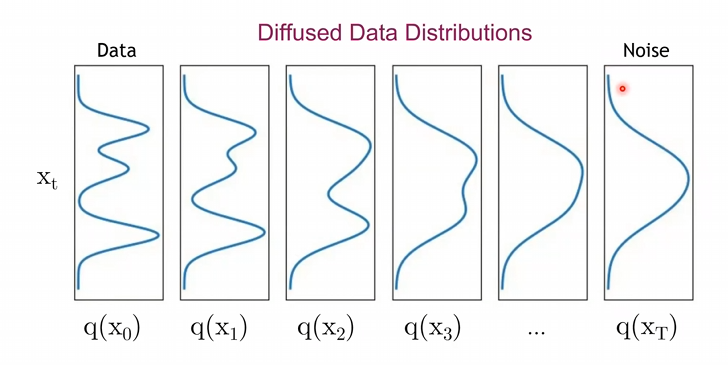
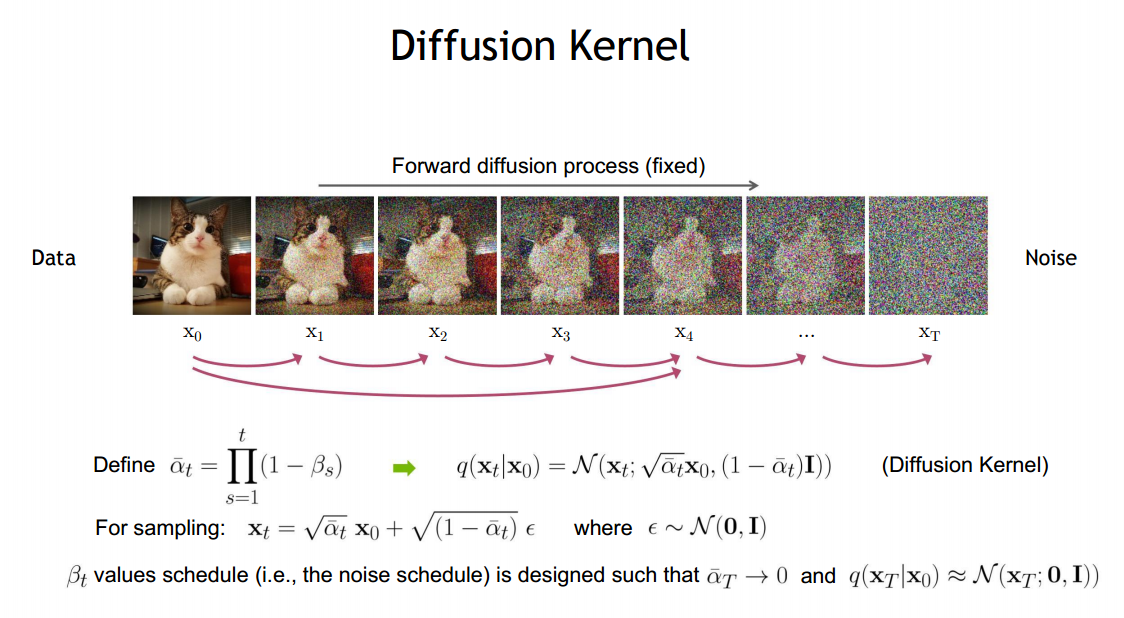
• DDPM의 이론 : TimeStep마다 약간의 노이즈를 추가한다면, 특정 TimeStep으로 한번에 노이즈를 추가한다면 $\mathbf{x_t}$를 얻을 수 있음 [$x_t$->$x_0$]
• 해당 방법으로 $x_t$를 $\mathbf{x_0}$에 따라 $\beta_t$가 아닌 $\alpha_t$로 표현 가능해짐
  

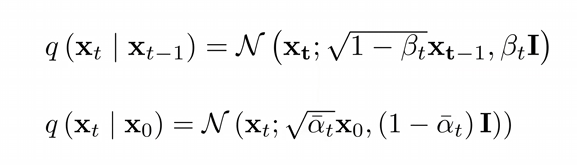
Reverse Process

• 가정 : Step이 매우 작기 때문에, Forward가 아닌 Reverse 또한 가우시안일 것임
  
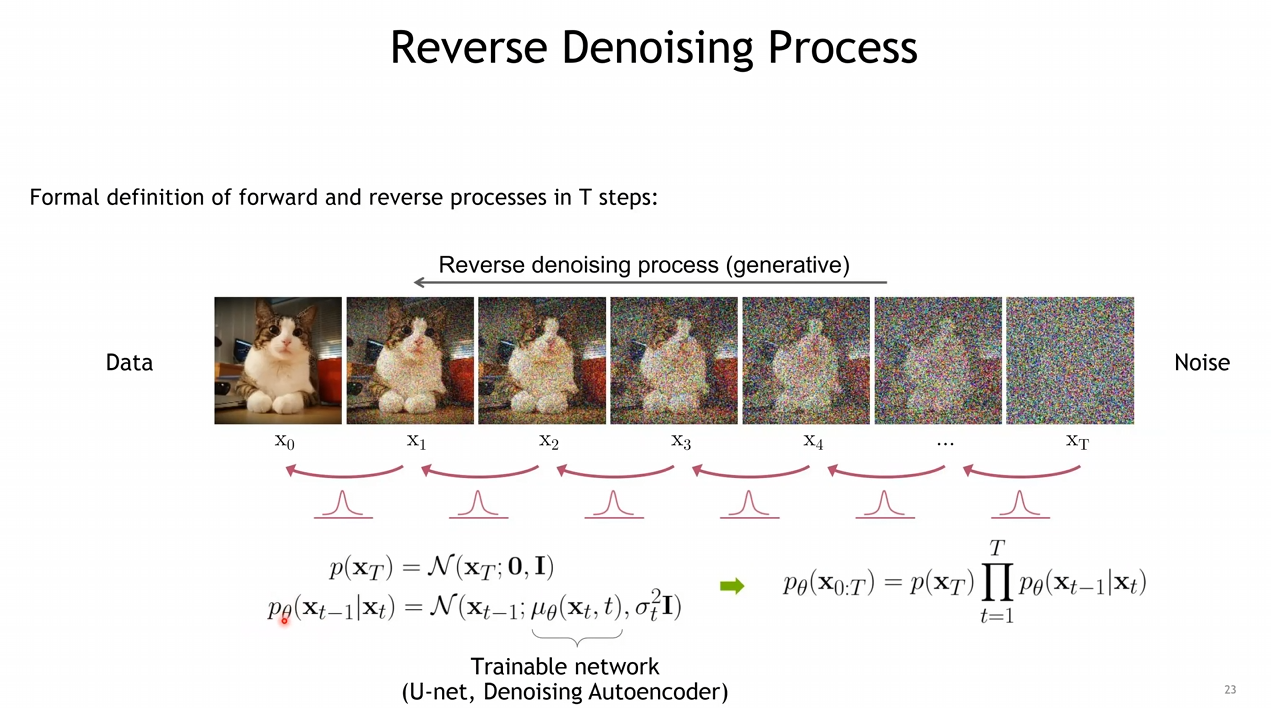
• Reverse를 하는 과정 또한 가우시안이라면, "평균과 분산은 어떻게 학습할 것인가"가 중요함

"평균과 분산은 어떻게 학습할 것인가"

• VAE에서 사용되었던 Variational upper bound를 이용하여 학습을 진행
  
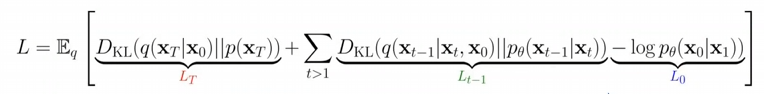
• $L_T$ : $q(\mathbf{x_T})$와 $p(\mathbf{x_T})$는 결국 둘 다 가우시안 노이즈로 둘 사이의 KL을 구하는 것은 의미가 없기에 사용되지 않음
• $L_{t-1}$ : $q(\mathbf{x_{t-1}}|\mathbf{x_t}, \mathbf{x_0})$과 $p_{\theta}(\mathbf{x_{t-1}}|\mathbf{x_t})$를 가우시안 분포로 가정하고 둘 사이의 KL을 구함

• 1번으로부터 별 모양의 수식(한 번에 여러 스텝의 노이즈를 계산한)을 통해 2번 수식으로 유도할 수 있음
• Reverse Process가 가우시안 모델이라 가정했을 때, 해당 가우시안 모델의 평균을 구하는 것을 목표로 하기에 3번과 같은 모델링이 가능함 -> Noise-Prediction이 가능

• 가우시안 모델의 평균을 예측하기 위해 식을 세우던 도중, 각 스텝 사이의 노이즈를 예측하면 된다는 결론이 도출

Training

• 매 스텝마다 가우시안 노이즈 $\epsilon$를 샘플링하여 이미지에 time step $t$에 맞춰 노이즈를 더함
• 네트워크는 어떤 노이즈가 더해졌는지 예측하도록 학습됨

Sampling

• 샘플링은 평균을 기반으로 샘플링을 진행함

Reverse Denoising Process

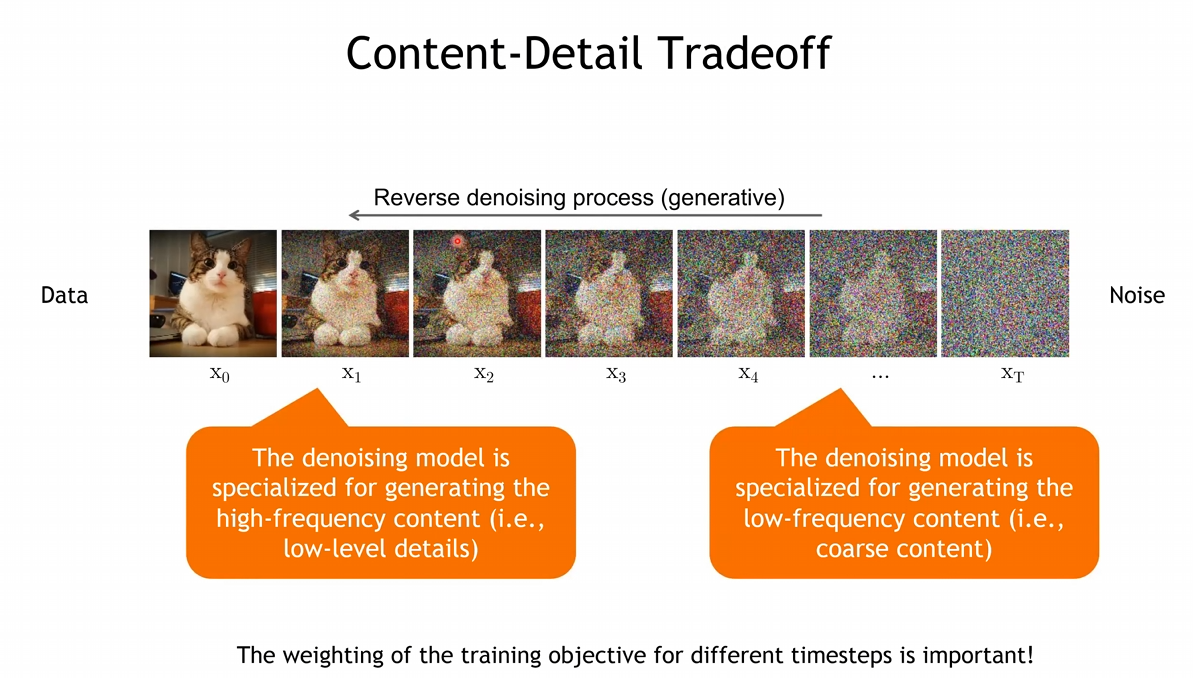
• 어떠한 Contents를 생성할 것인지는, $\mathbf{x_t}$에 근접한 과정에서 이루어짐
• 반대로 $\mathbf{x_0}$에 가까워 질 수록 Denoising에 근접한 Task를 수행함

DDPM(Denoising Diffusion Probailistic Models)

• Network Architectures : U-Net
• Objective weighting : Loss 앞의 값들 (1로 고정)
• Diffusion parameters(noise schedule)
  
• Reverse Process를 모델에게 학습을 통해, 각 Time step $t$의 가우시안 커널의 평균과 분산을 예측하도록 학습
• $\mu_{\theta}(\mathbf{x_t}, t)$ : Reverse Process의 가우시안 커널의 평균
• $L_{simple}$ : $\mu_{\theta}(\mathbf{x_t}, t)$를 통해 Noise를 예측하는 Loss 함수

2. DDIM

---

Non-Markovian Diffusion Process로, Loss는 Original Diffusion과 똑같이 사용하되, Sampling만 DDIM의 방식으로 진행한다는 장점을 갖는 방법

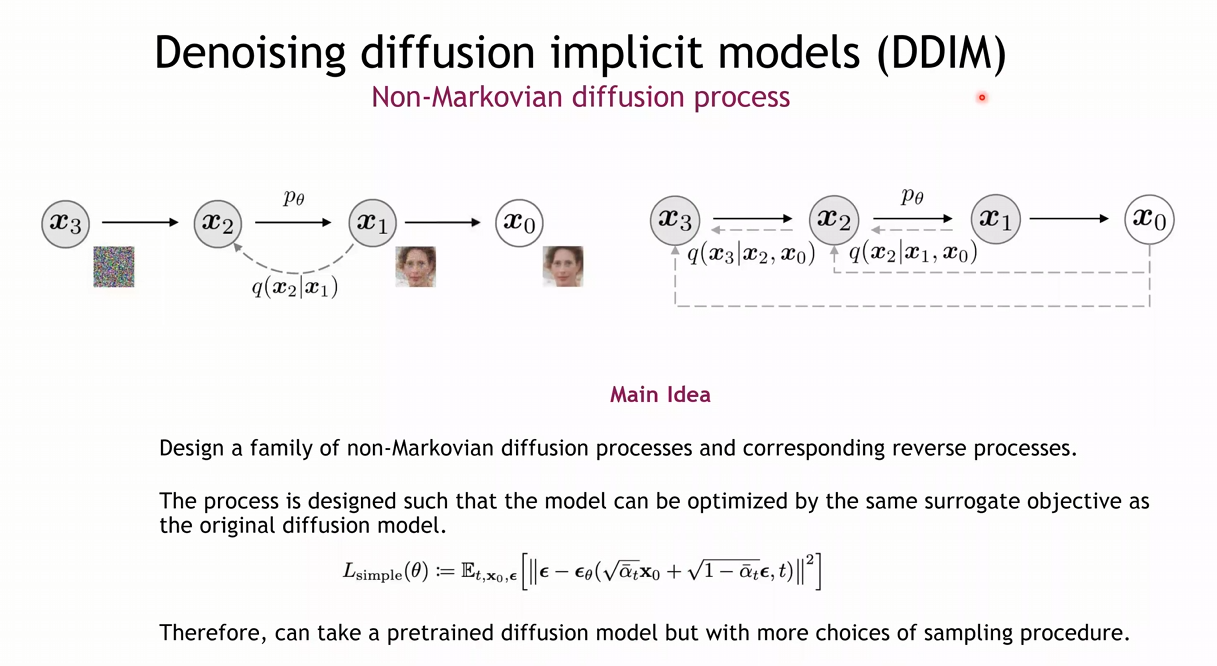
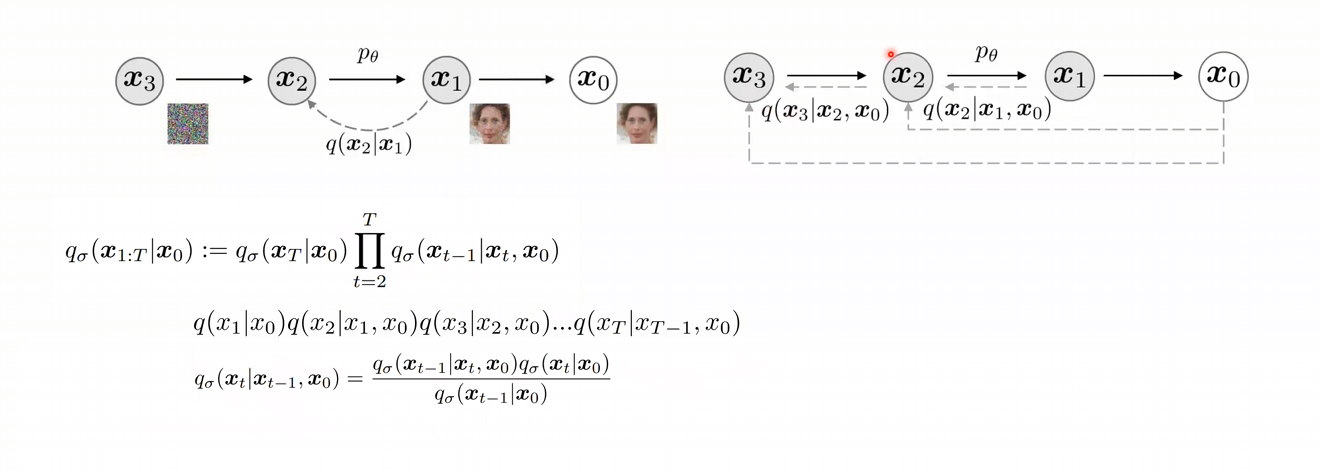
• DDPM에서는 $q_{\sigma}$를 베이즈룰과 마르코프 법칙을 사용하여 평균과 분산을 구한 뒤, 정의를 내렸음
• DDIM에서는 $q_{\sigma}$를 바로 이전 Step과 $\mathbf{x_0}$의 $q$만을 사용하여 정의를 내릴 수 있음

DDIM Sampler

• Random Noise가 $\sigma_t$와의 곱으로 이루어져 있는데, 이는 확률적인 변수이다보니 이전에 이미지를 생성하는 과정에서 deterministic하지 못한 모습을 보인듯 함
• 따라서 $\sigma_t$를 0으로 보냄으로써, 노이즈와 이미지가 1대1 맵핑이 되는 듯한 효과를 줌
• 그에 따라서 노이즈로부터 여러 Step을 건너뛸 수 있는 Sampling을 할 수 있다는 장점이 있음
  -> Deterministic, Fast Sampling

3. Score-based models

---

Diffusion과 Score-based와 같은 개념이며, 정의되어 있는 식은 다르나 결과적으로는 수학적으로 일치하는 관계임

• Forward Diffusion Process는 샘플링 하는 과정은 SDE로 표현이 가능함
• SDE : 하나 이상의 term이 stochastic process인 미분방정식, 즉 randomness를 포함하고 있는 미분방정식
  
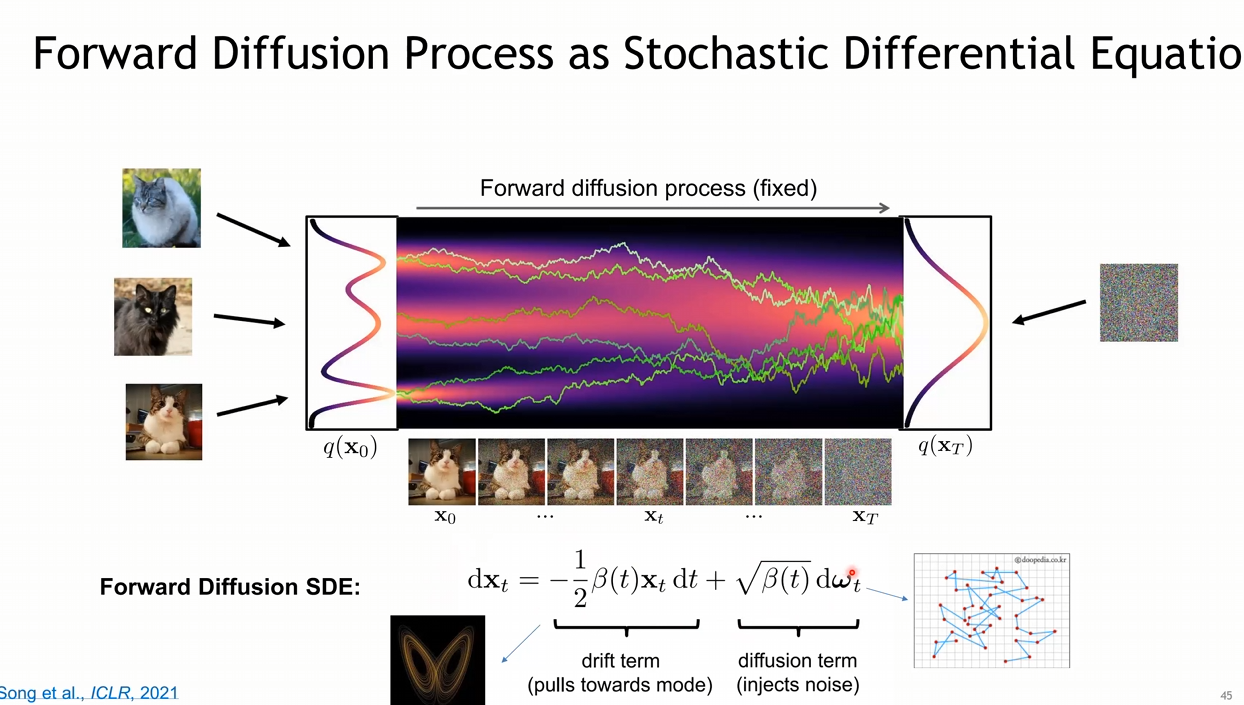
• 어떠한 영상을 결국 Foward Diffusion SDE를 통해, 가우시안 분포로 만들게 되고 이 때, Randomness를 가진 Diffusion Term을 사용함

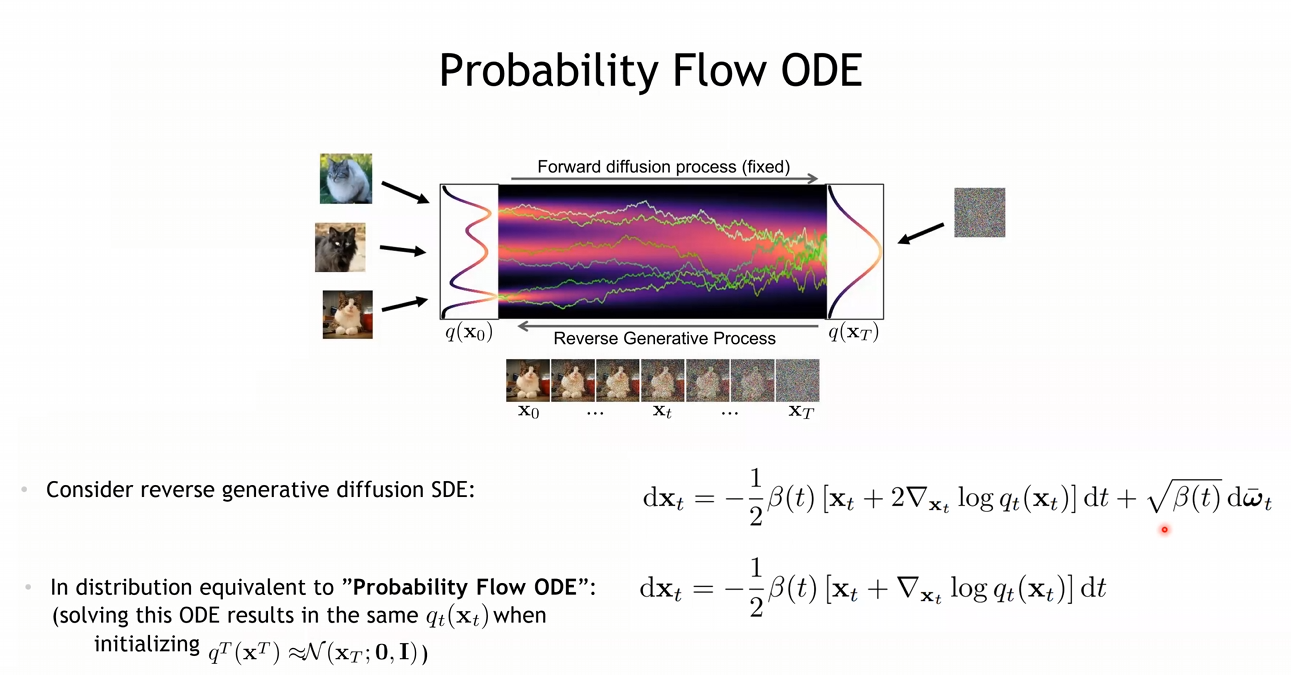
• DDIM처럼 이러한 Stochastic한 SDE를 좀 더 Deterministic하게 변경하려는 시도를 함.
  즉, SDE-> ODE (ODE: 어떤 variable과 그것의 미분으로 구성된 방정식)
  
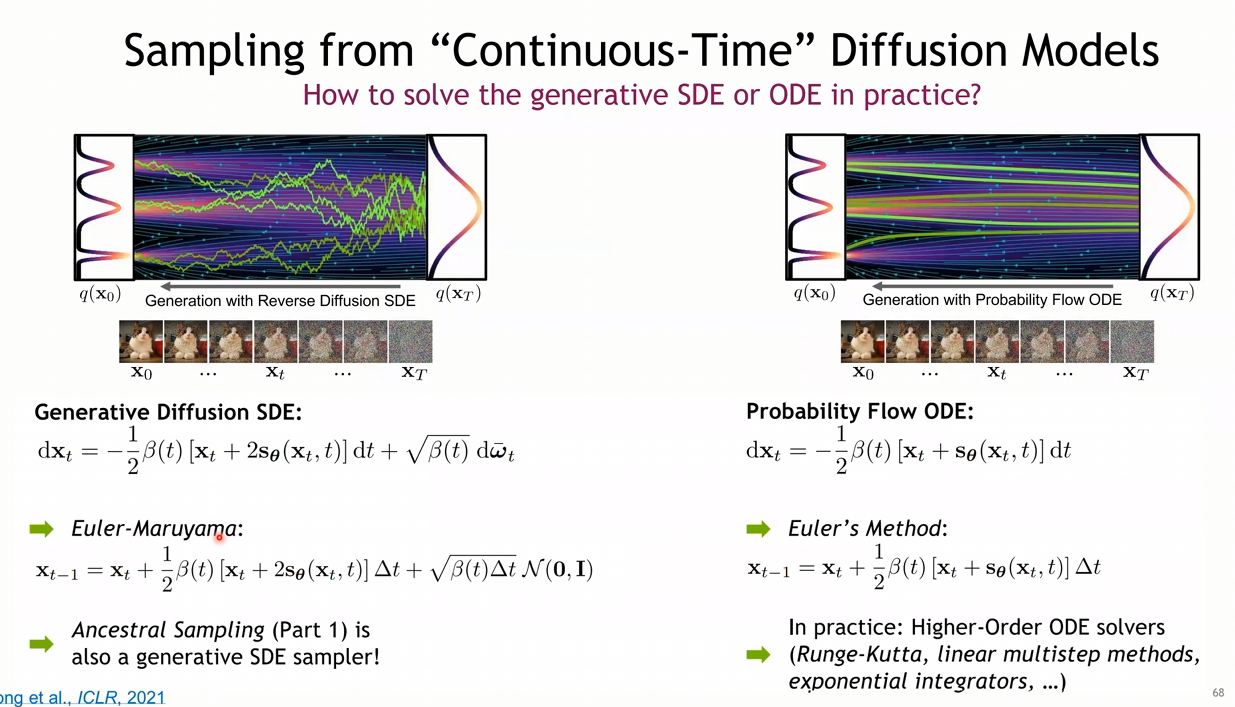
• 좌측 그림과 우측 그림을 봤을 때, Stochastic한 SDE에 비해 ODE가 매칭이 되는 듯한 결과를 보임

4. Conditional diffusion models

---

Conditional diffusion models

• 어떻게 원하는 대로 Conditional하게 Reverse할 수 있을 까?
  
• SDE의 Reverse process인 위의 식의 주황색 박스를 베이즈 룰을 통해, 아래와 같은 수식으로 분리할 수 있음
• 여기서 학습 가능한 $\nabla_\mathbf x \log{p_t(\mathbf y |\mathbf x)}$에 Y가 Controll signal인 것을 이용하여 Conditional하게 조건을 줄 수 있음
  
• Classifier의 Gradient값을 더하여 Sampling을 하게 되면 해당 클래스의 이미지를 뽑아낼 수 있다는 것이 Main Idea임
  
• $\mathbf y$는 다양하게 사용될 수 있음 (Text, Mask 등..)
  

Diffusion Summary
1. GAN과 유사하거나 더 나은 퀄리티를 보임
2. Flow Model과 유사함 -> Likelyhood를 계산할 수 있음, Latent codes(Noise) 변경을 통해 조절 가능
3. Controllable Generation :

• $\mathbf y$에 따라 Inpainting, Class-conditional Generation, Colorization 등에 사용 가능함
• 새로운 Task에 따라 Score-based Models을 학습시킬 필요가 없음

Tree

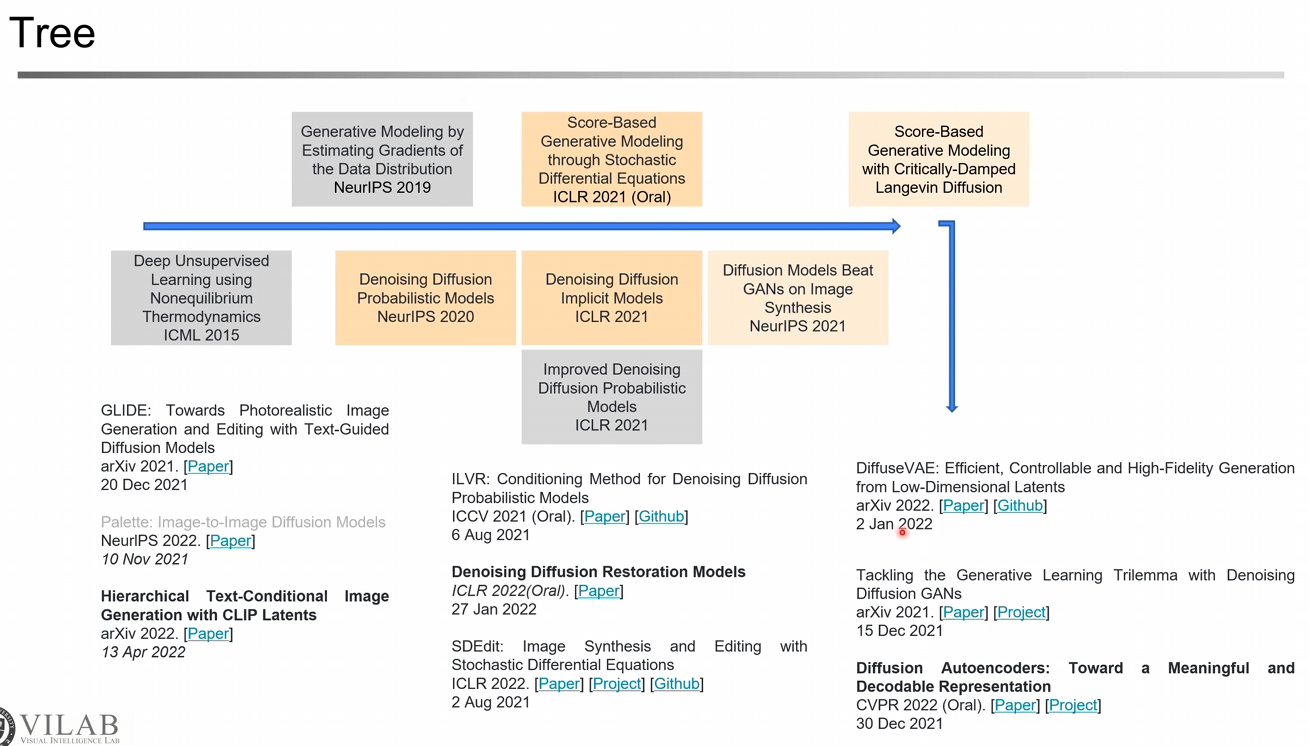
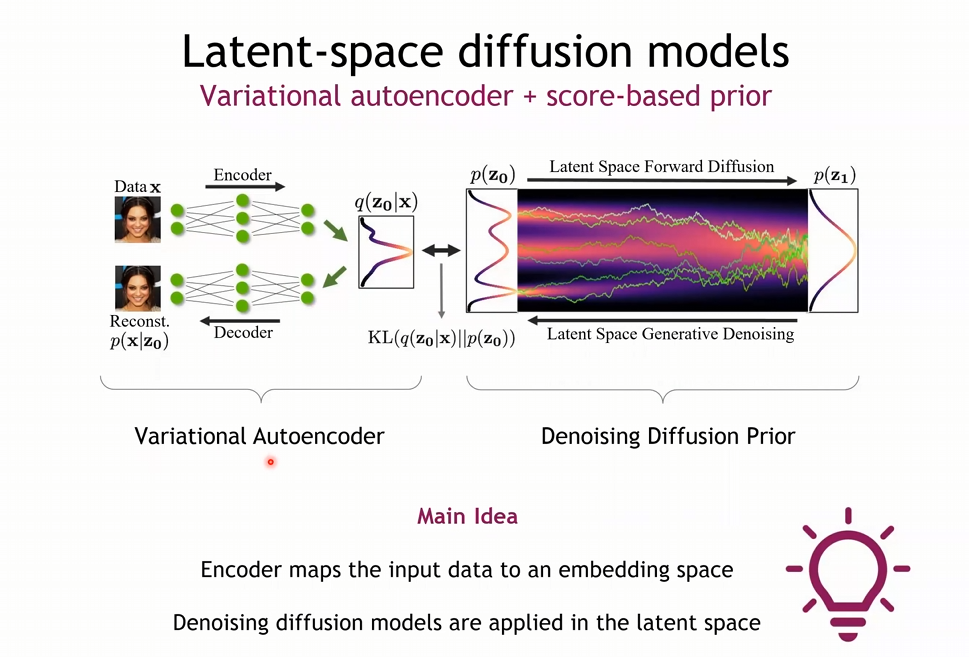
• Latent Diffusion : VAE를 통해 Latent를 만들고 이를 Diffusion Task에 사용
• Classifier-free guidance : 학습 과정에 Classifier-free guidance를 추가 -> DALLE, DALLE2
• Cascaded Genertaion : 작은 이미지를 생성해놓고 키워나가는 방식
• GLIDE : CLIP Guidance, Text Input
• DALLE2 : 텍스트의 Latent는 동일하지만 매번 다른 이미지를 생성할 수 있도록 Latent Representation을 시도
• Diffusion Autoencoders : Encoder로부터 semantic latent를 직접적으로 만들며 해결