강의 복습 내용
[DAY 7] 경사하강법
[AI Math 3강] 경사하강법(순한맛)
- 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법입니다.
- 미분은 함수 f의 주어진 점 (x, f(x))에서의 접선의 기울기를 구합니다.
- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있습니다.
- 미분값을 더하면 경사상승법(gradient ascent)이라 하며 함수의 극대값의 위치를 구할 때 사용합니다.
- 미분값을 빼면 경사하강법(gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용합니다.
- 경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈춥니다.
- 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법입니다.
- 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용합니다.
- 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있습니다.
- 경사하강법: 알고리즘
# gradient: 그레디언트 벡터를 계산하는 함수
# init: 시작점
# lr: 학습률
# eps: 알고리즘 종료조건
var = init
grad = gradient(var)
while(norm(grad) > eps):
var = var - lr * grad
grad = gradient(var)[AI Math 4강] 경사하강법(매운맛)
- 선형회귀의 목적식은 ∥y − Xβ∥2이고 이를 최소화하는 β를 찾아야 합니다.
- 이제 목적식을 최소화하는 β를 구하는 경사하강법 알고리즘은 다음과 같습니다.
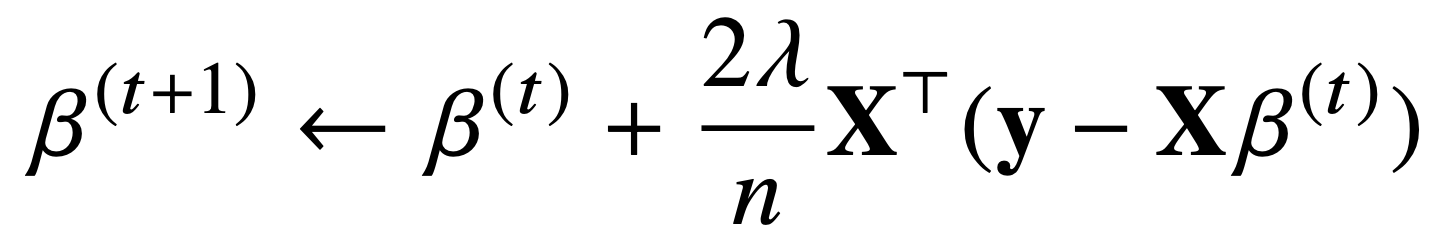
- 경사하강법 기반 선형회귀 알고리즘
# norm: L2-노름을 계산하는 함수
# lr: 학습률
# T: 학습횟수
for t in range(T):
error = y - X @ beta
grad = - transpose(X) @ error
beta = beta - lr * grad- 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있습니다.
- 특히 선형회귀의 경우 목적식 ∥y − Xβ∥2은 회귀계수 β에 대해 볼록함수이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장됩니다.
- 하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않습니다.
- 확률적 경사하강법(stochastic gradient descent)은 모든 데이터를 사용해서 업데이트하는 대신 데이터 한개 또는 일부 활용하여 업데이트합니다.
- 볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화할 수 있습니다.
- SGD는 데이터의 일부를 가지고 패러미터를 업데이트하기 때문에 연산자원 을 좀 더 효율적으로 활용하는데 도움이 됩니다.
- 확률적 경사하강법의 원리: 미니배치 연산
- 경사하강법은 전체데이터 𝒟=(X, y)를 가지고 목적식의 그레디언트 벡터인 ∇θL(𝒟,θ)를 계산합니다.
- SGD는 미니배치 𝒟(b)=(X(b), y(b))⊂𝒟를 가지고 그레디언트 벡터를 계산합니다.
- 미니배치는 확률적으로 선택하므로 목적식 모양이 바뀌게 됩니다.
- SGD는 볼록이 아닌 목적식에서도 사용 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적입니다
피어 세션 정리
강의 리뷰 및 Q&A
- [AI Math 3강] 경사하강법(순한맛)
- [AI Math 4강] 경사하강법(매운맛)
퀴즈 결과 회고
[AI Math 3-4강 퀴즈] 경사하강법-1~5
- 편미분 계산 (O)
ans: 9
- 미분이 가능한 함수 f에 대해, 주어진 점 (x,f(x))에서의 접선의 기울기가 음수라면, x를 증가시키면 함수값 f(x)이 증가한다. (O)
ans: 아니오
- 함수의 극소값의 위치를 구할 때 사용하는 방법을 고르시오. (O)
ans: 경사하강법
- 경사하강법을 사용하여 구한 함수의 극소값의 위치는 해당 함수의 최소값의 위치가 아닐 수 있다. (O)
ans: 예
- 그래디언트 벡터 계산 (O)
ans: 3
총평
피어 세션의 강의 리뷰 및 Q&A에서 경사 상승법에 대한 내용을 준비했습니다.
그 덕분에, 경사 하강법의 새로운 응용 방법에 대해서 배울 수 있었고 생각해볼 수 있었습니다.
그리고 내일 피어 세션에서 브런치 사용자를 위한 글 추천 대회 개요와 [토크ON세미나] 추천시스템 분석 입문하기의 내용을 발표하기로 했습니다.
갑작스럽게 준비하게 된 발표지만, 다른 조원들이 하나라도 배우는 것이 있도록 준비할 계획입니다.
오늘보다 더 성장한 내일의 저를 기대하며, 내일 뵙도록 하겠습니다.
읽어주셔서 감사합니다!
