
탐색 알고리즘
주어진 자료구조에서 원하는 정보를 찾거나 특정 목적을 달성하기 위해 시스템적으로 자료를 조사하는 알고리즘이다.
그래프
정점과 간선으로 구성된 한정된 자료구조이다. 이때 각각의 지점을 정점이라고 하며, 정점과 정점을 연결하는 선을 간선이라고 부른다.
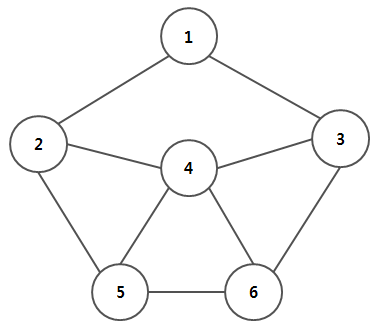
1. DFS(Depth-First Search)
DFS는 한 경로를 따라 최대한 깊숙이 들어가면서 탐색을 진행한 후, 더 이상 진행할 수 없을 때 다시 돌아가 다른 경로를 탐색하는 방식이다.
- 깊이 우선 탐색
- 스택 이용 → 재귀 함수 활용
O(n)의 시간복잡도
DFS 동작 과정
DFS는 특정 시작 노드에서 출발하여 그래프를 탐색하는 알고리즘으로, 다음과 같은 과정을 따른다.
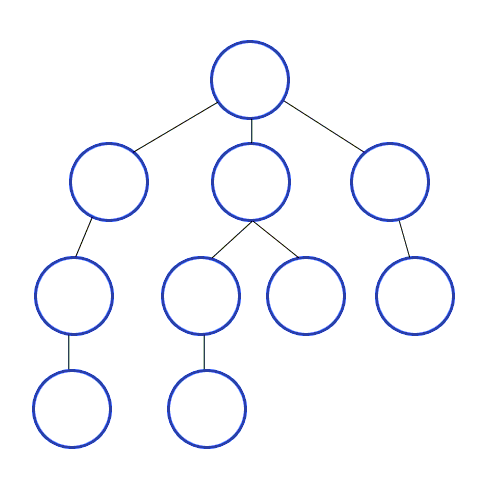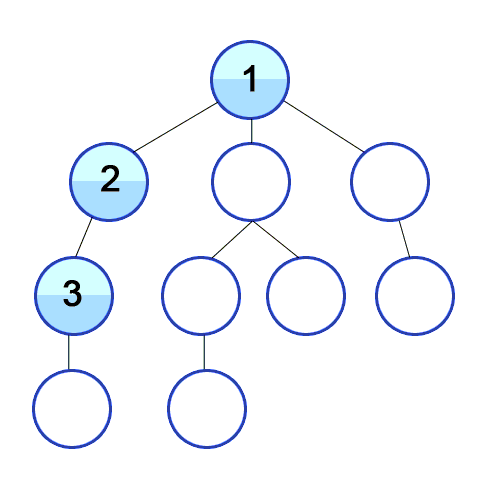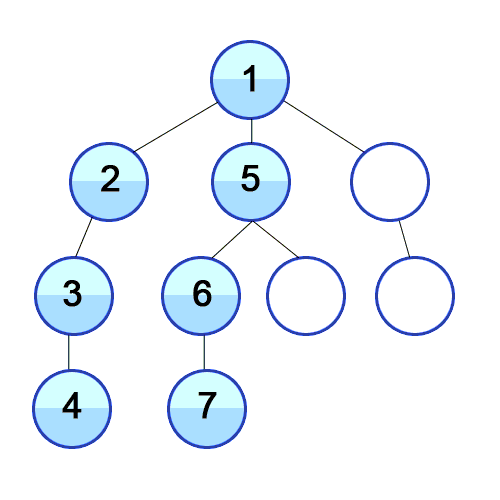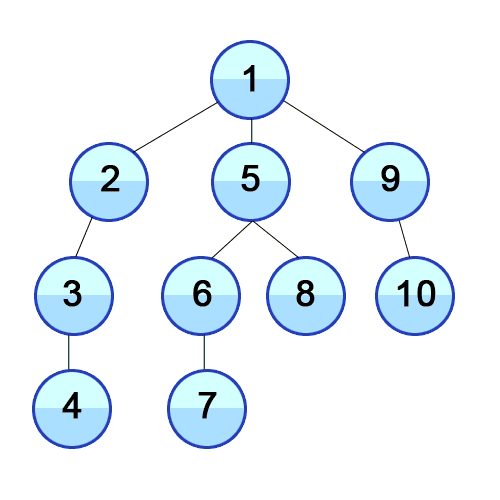
- 시작 노드를 스택에 삽입하고, 해당 노드를 방문한 것으로 표시한다.
- 스택의 최상단 노드와 인접한 노드를 확인한다.
- 인접한 노드 중에서 방문하지 않은 노드가 있으면, 해당 노드를 임의로 선택한다.
- 인접한 노드 중에서 방문하지 않은 노드가 없으면, 스택에서 최상단 노드를 꺼낸다.
- 선택한 노드를 시작 노드로 삼아 다시 DFS를 수행한다.
(임의로 선택한 노드를 스택에 삽입하고 방문한 것으로 표시한다.) - 더 이상 방문하지 않은 노드가 없을 때까지 위 과정을 반복한다.
DFS 자바스크립트 구현
function dfs(graph, start, visited) {
if (!visited[start]) {
console.log(start);
visited[start] = true;
for (let neighbor of graph[start]) {
dfs(graph, neighbor, visited);
}
}
}
const graph = {
1: [2, 3],
2: [4, 5],
3: [],
4: [],
5: [6],
6: [],
};
const visited = {};
dfs(graph, 1, visited);DFS 장단점
장점
- 간선의 수가 적은 경우에는 다른 알고리즘보다 간결하게 구현될 수 있다.
- 한 경로를 따라 탐색하다가 더 이상 진행할 수 없으면 다른 경로로 돌아와 탐색하기 때문에 경로 추적에 용이하다.
단점
- 순환 그래프의 경우, 모든 노드를 방문할 수 없는 경우가 발생할 수 있다.
- 경로의 길이가 길어질수록 최단 경로를 찾는 데 시간이 오래 걸릴 수 있다.
- 재귀를 사용하는 경우 깊이가 매우 깊으면 스택 오버플로우가 발생할 수 있다.
2. BFS(Breadth-First Search)
BFS는 시작 노드에서 출발하여 인접한 모든 노드를 먼저 탐색하고, 그 다음에는 그 인접한 노드들의 인접한 노드들을 차례로 탐색하는 방식이다.
- 너비 우선 탐색
- 큐 이용
O(n)의 시간복잡도
BFS 동작 과정
BFS는 특정 시작 노드에서 출발하여 그래프를 탐색하는 알고리즘으로, 다음과 같은 과정을 따른다.
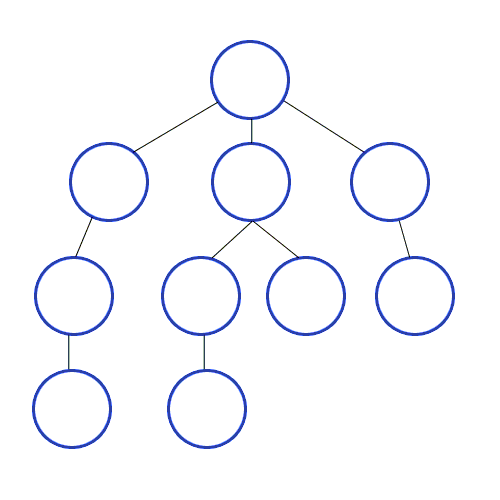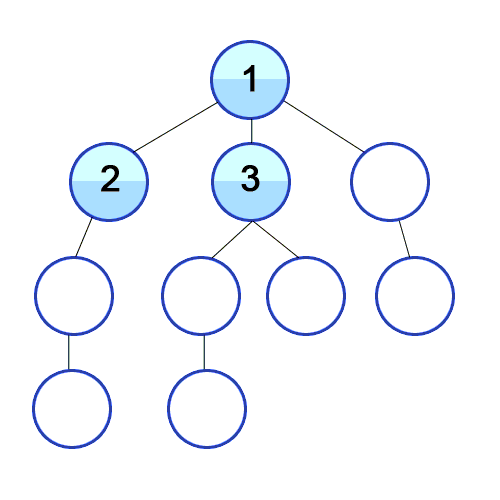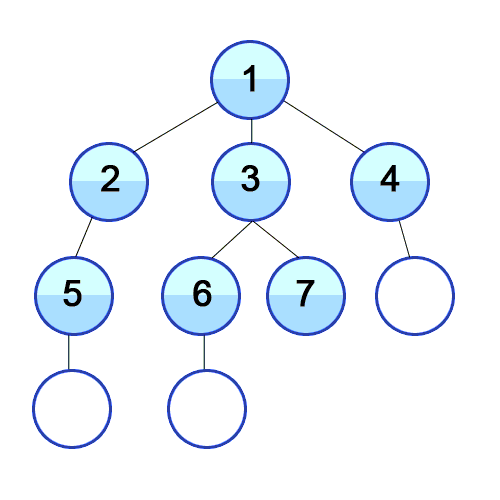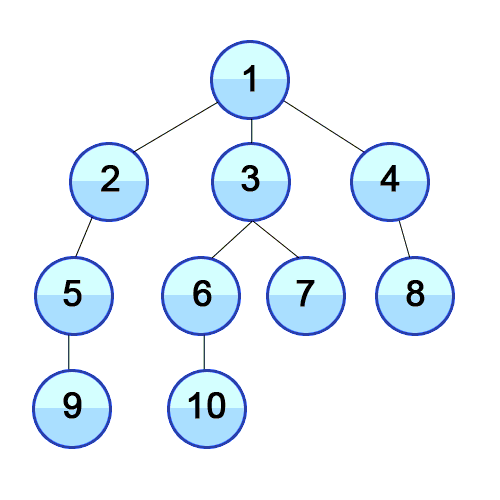
- 시작 노드를 큐에 삽입하고, 해당 노드를 방문한 것으로 표시한다.
- 큐에서 노드를 꺼내고, 해당 노드와 인접한 노드들 중 방문하지 않은 노드를 모두 큐에 넣고 방문 처리한다.
- 큐가 비어 2번 과정을 더 이상 수행할 수 없을 때까지 위 과정을 반복한다.
BFS 자바스크립트 구현
function bfs(graph, start) {
const queue = [start];
const visited = new Set();
while (queue.length > 0) {
const node = queue.shift();
if (!visited.has(node)) {
console.log(node);
visited.add(node);
for (let neighbor of graph[node]) {
if (!visited.has(neighbor)) {
queue.push(neighbor);
}
}
}
}
}
// 호출 예시
const graph = {
1: [2, 3],
2: [4, 5],
3: [],
4: [],
5: [6],
6: [],
};
bfs(graph, 1);BFS 장단점
장점
- 시작 노드로부터 가까운 노드부터 탐색하기 때문에 최단 경로를 찾는데 유리하다.
- 순한 그래프에서도 안전하게 탐색할 수 있다.
단점
- 큐를 사용하기 때문에 메모리 사용량이 꽤 크다.
- 특히, 그래프의 깊이가 깊은 경우 메모리의 부담이 커질 수 있다.
DFS와 BFS
- DFS는 그래프에서 특정 경로의 존재 여부를 확인하거나, 순서가 중요한 경우에 활용된다.
- BFS는 그래프에서 최단 거리를 찾을 때 유용하다. (DFS의 경우 처음 발견한 해답이 최단 거리가 아닐 수도 있지만, BFS는 현재 노드에서 가까운 곳부터 찾기 때문에 가장 먼저 발견한 해답이 곧 최단 거리이기 때문이다.)
