
📌 소수(Prime Number)란?
소수는 1과 자기 자신만으로 나누어 떨어지는 양의 정수이다. 즉, 소수의 약수는 1과 자기 자신만 존재한다.
예를 들어,
- 2의 약수는 1과 2이므로 2는 소수이다.
- 3의 약수는 1과 3이므로 3은 소수이다.
- 4의 약수는 1, 2, 4이므로 4는 소수가 아니다.
- 5의 약수는 1과 5이므로 5는 소수이다.
📌 소수 판별
1. 반복문(n-1)
첫 번째 방법은 2부터 n-1까지 확인하는 방법이다.
소수의 정의에 따르면 정수 n이 소수이기 위해서는 n을 2부터 n-1까지 순서대로 나누었을 때, 나누어 떨어지는 수가 있어서는 안 된다. 즉, n을 2부터 n-1까지 순서대로 나누었을 때, 나머지가 0이 되는 수가 있어서는 안 된다.
const isPrime = (n) => {
for (let i = 2; i < n; i++) {
if (num % i === 0) return false;
}
return true;
};이러한 방식을 이용하면 시간 복잡도는 O(n) 이다.
2. 반복문(n/2)
두 번째 방법은 2부터 n/2까지만 확인하는 방법이다. n의 약수는 자신의 절반을 넘을 수 없다.
예를 들어, n이 16이라면 n/2인 8보다 큰 수로 나누었을 땐, 자기 자신 16을 제외하고는 나누어 떨어지는 경우가 없다. 즉, n/2를 초과하는 수로 나누면 나머지가 0이 되는 수가 나올 수 없다.
const isPrime = (n) => {
for (let i = 2; i < n / 2; i++) {
if (num % i === 0) return false;
}
return true;
};이러한 방식을 이용하면 최대 n/2번 조회하지만, 시간 복잡도는 상수를 제외하므로 시간 복잡도는 O(n) 이다.
3. 반복문(√n)
세 번째 방법은 2부터 √n까지만 확인하는 방법이다.
이는 약수의 대칭성을 이용한 방법이다. 약수는 짝으로 존재한다. 따라서 쌍을 이루는 약수 중 한 쪽만 찾으면 나머지 한 쪽은 확인하지 않아도 된다.
예를 들어, n이 20이라면 n의 약수 쌍은 1 * 20 , 2 * 10 , 4 * 5 이다. √20 = 4.xxx 이므로 4까지만 검사해도 약수의 대칭성에 의해 5, 10, 20은 20의 약수인 것이 보장되기 때문에 확인하지 않아도 된다.
const isPrime = (n) => {
for (let i = 2; i < Math.sqrt(n); i++) {
if (num % i === 0) return false;
}
return true;
};Math.sqrt()메서드는 숫자의 제곱근을 반환한다. 만약 n이 음수면NaN을 반환한다.
이러한 방식을 이용하면 시간 복잡도는 O(√n) 이다.
4. 에라토스테네스의 체
네 번째 방법은 에라코스테네스의 체를 활용하는 방법이다.
에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법이다.
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
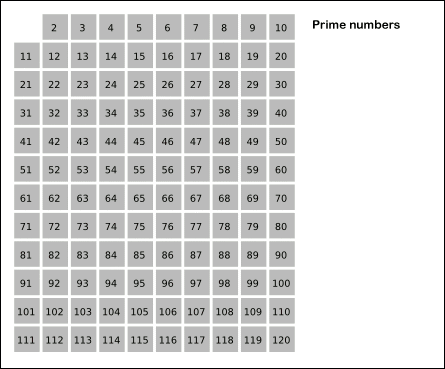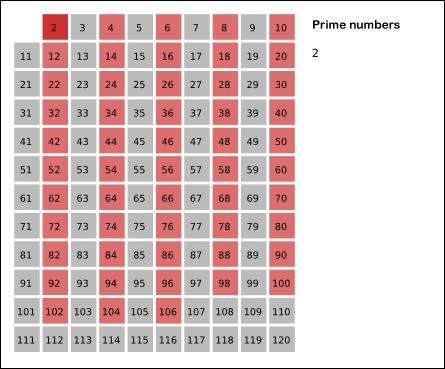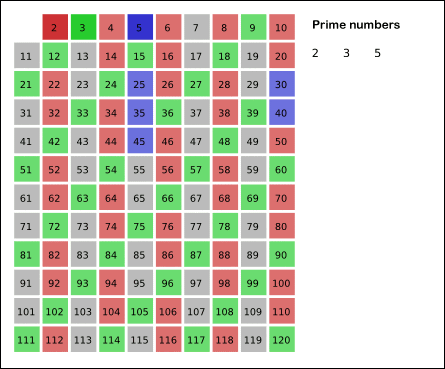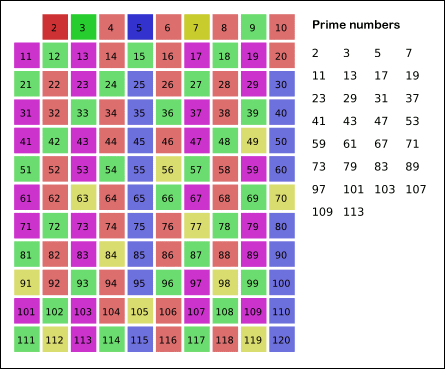
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)
위 그림의 경우, 11^2 > 120이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 4, 5의 배수를 지우고 남는 수는 모두 소수이다.
결국, 2부터 n의 제곱근까지 반복하며 해당 수의 배수를 지우고 남는 수를 구하는 것이다.
const solution = (n) => {
// 인덱스가 0부터 n까지인 배열 생성 (인덱스 0과 1은 false, 나머지는 true)
let arr = Array(n + 1).fill(true).fill(false, 0, 2);
// i는 2부터 n의 제곱근까지만 반복
for (let i = 2; i * i <= n; i++) {
if (arr[i]) {
// i의 배수는 false로 변경
for (let j = i * i; j <= n; j += i) {
arr[j] = false;
}
}
}
// 0부터 n까지의 숫자 중 소수만 true인 배열 반환
return arr;
};let isPrime = solution(100);
// 소수의 개수 구하기
let count = isPrimes.filter(e => e).length; // 25
// 소수 반환하기
let primes = isPrimes.map((v, i) => (v) ? i : 0).filter(e => e);
// [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]참조
