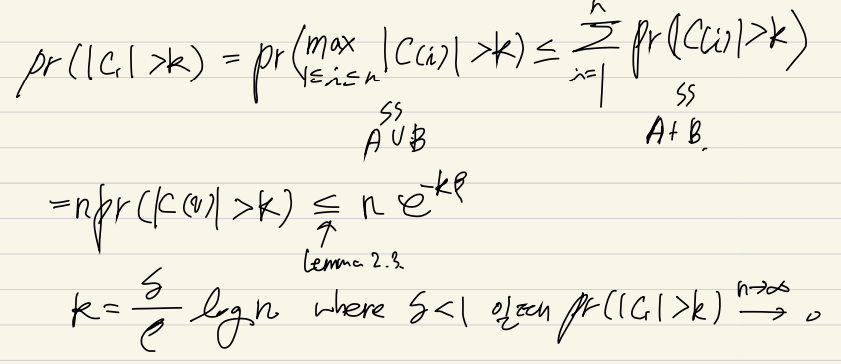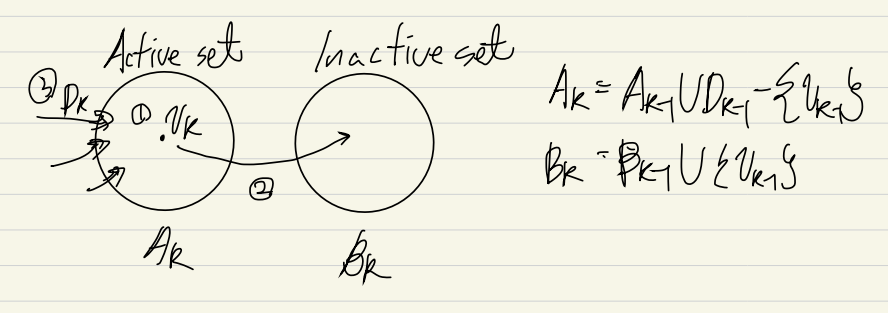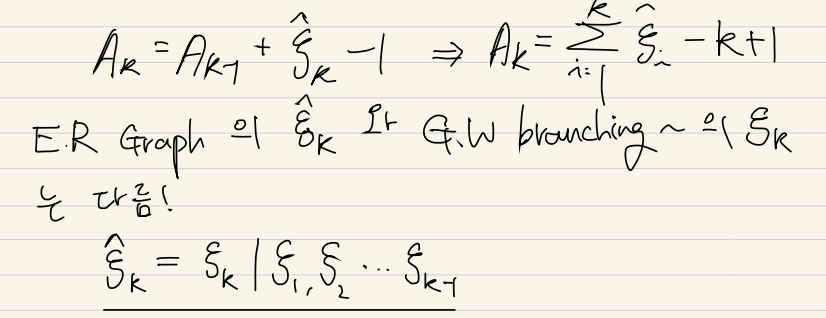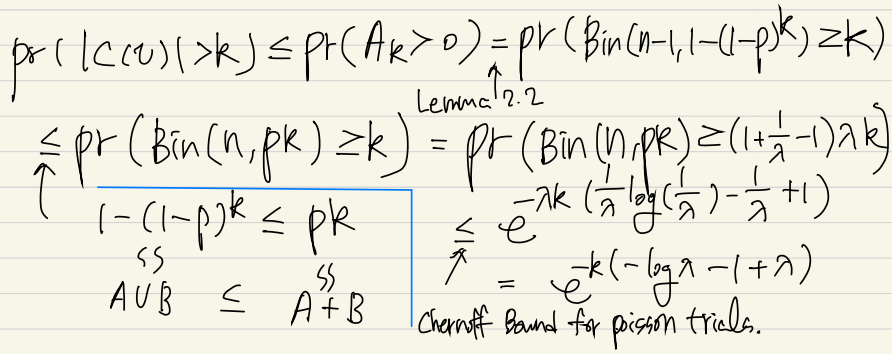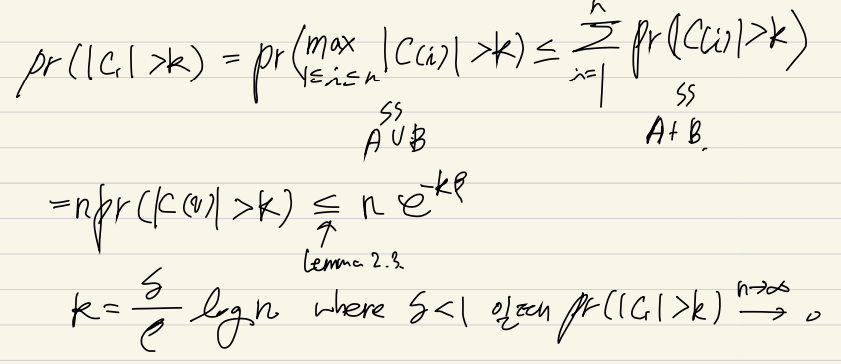Complex Network 분석(3. Giant Component)

강의 출처

Subcritical regime ( $\lambda < 1$ )

Thm.1

$\lambda < 1$ 일떄 어떤 상수 a = a($\lambda$) 에 대하여

$Pr(|C_1|\le alog(n))\to1 \>\> as\>n\to\infty$ 를 만족한다.
(= 만약 n이 충분히 크다면 $|C_1|\le alog(n)$ 큰 확률(with high probability)로 일어난다.)

$C_1$ : largest component의 node의 집합이다.

접근 방식

G.W branching process + one-by-one exploration

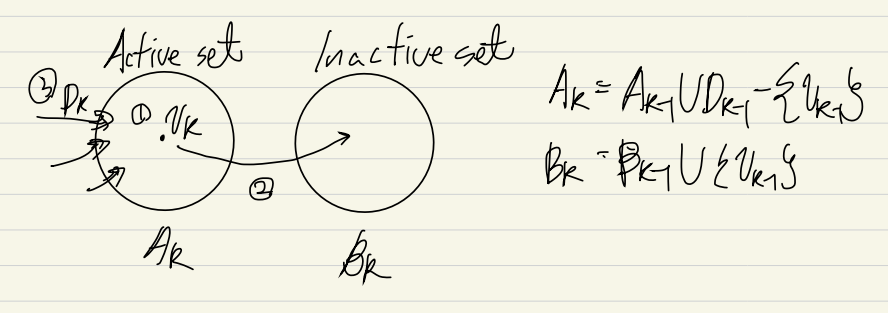
(1) step k에 $A_k$에서 아무 node $v_{k}$를 선택한다.
(2) $v_{k}$ 을 $B_{k}$ 에 넣는다.
(3) $v_{k}$ 의 모든 인접 node를 active set에 넣는다.
초기 조건 : $A_{0}=\{v_0\}, B_0=\emptyset$
$D_k$ : $v_{k}$ 의 모든 인접 node 의 집합, $|D_k| = \hat\xi_k$

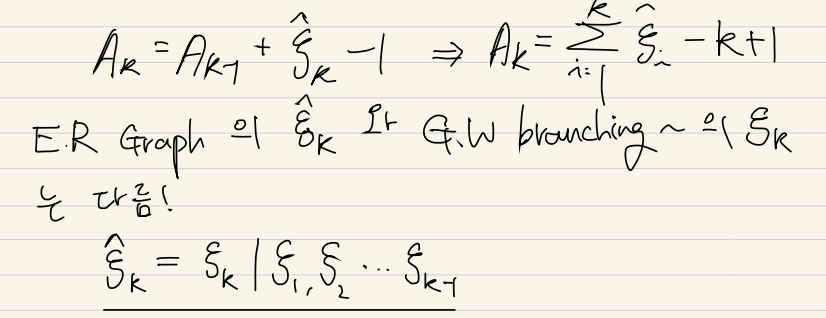
Lemma 2.2 $A_k+k-1 \sim Bin(n-1,1-(1-p)^k)$

Lemma 2.3 $Pr(|C(v)|> k)\le exp(-\beta k), \beta = -log(\lambda)-1+\lambda$

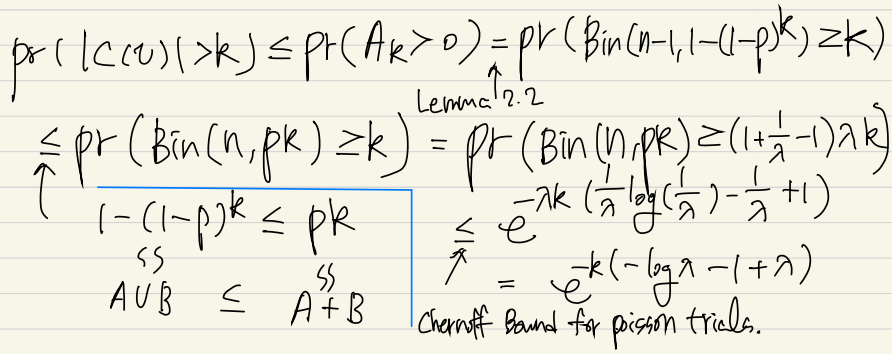
Thm.1 proof