[TIL] DFS 알고리즘

DFS (Depth-First Search)

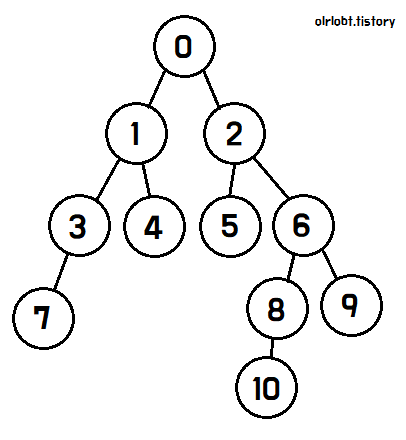
깊이 우선 탐색(DFS, Depth-First Search)이란 트리나 그래프를 탐색하는 기법 중 하나로, 시작 노드에서 자식의 노드들을 순서대로 탐색하면서 깊이를 우선으로 탐색하는 알고리즘이다.

깊이를 우선시하여 모든 경우의 수를 탐색하기 때문에, 완전탐색 알고리즘에 속하기는 하지만,
항상 완전탐색으로 사용되지는 않는다.

DFS는 주로 반복문을 활용하거나, 재귀문을 통하여 구현된다.

DFS의 탐색 과정

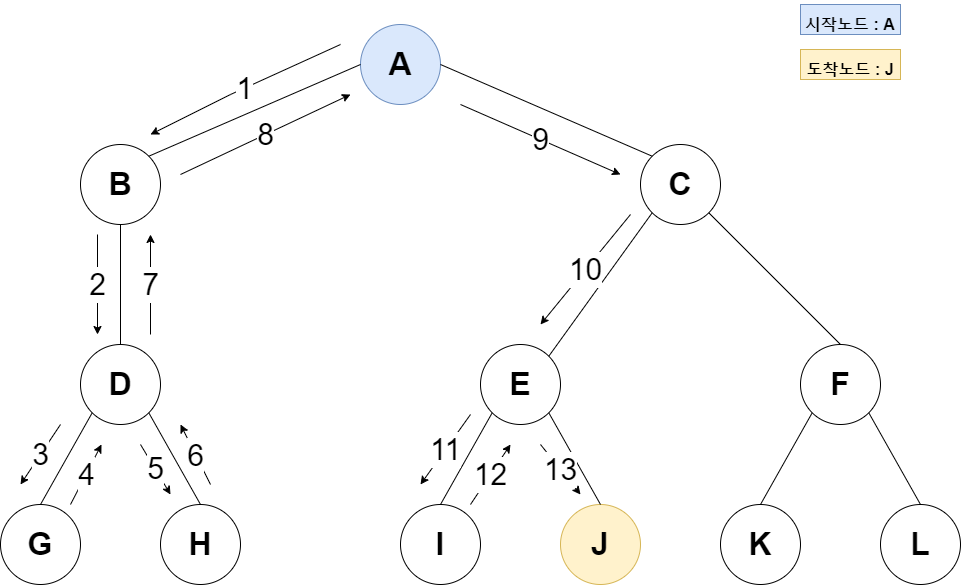
DFS의 기본 탐색 과정은 특정 정점에서 시작하여 역추적(backtracking) 하기 전에 각 분기를 따라 가능한 한 멀리 탐색하는 것이다. 탐색하는 과정은 다음과 같다.

1. 현재 노드를 방문한 것으로 표시한다.
2. 방문한 표시가 되어 있지 않은 각각의 인접한 정점을 탐색한다.
3. 더 이상 방문하지 않은 정점이 없으면 이전 정점으로 역추적(backtracking) 한다.
4. 모든 정점을 방문할 때까지 프로세스를 반복한다.

DFS의 장단점

DFS의 장점:

1. DFS는 현재 순회 중인 정점만 저장하는 스택 데이터 구조를 사용하기 때문에 BFS에 비해 메모리 공간을 덜 차지한다.
2. DFS는 목표가 특정 정점(또는 모든 정점)에 최대한 빨리 도달하는 것일 때 유용하다.
3. DFS를 사용하여 그래프에서 순환을 감지할 수 있다.

DFS의 단점:

1. 순환 그래프의 경우 DFS가 무한 루프에 빠질 수 있다.
2. DFS는 두 정점 사이의 최단 경로를 찾으려는 경우 사용하기에 가장 좋은 알고리즘이 아닐 수 있다.

DFS를 활용하기 적합한 문제

경로의 특징을 저장해둬야 하는 문제 (경로 상의 노드를 기억해야하는 문제)

ex) 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용한다.

검색 대상 그래프 큰 문제

ex) 목표노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있기 때문이다.