B-Tree, B+Tree, B*Tree

석형원·2024년 10월 11일

자료구조

📕 Self-balancing Tree

Binary Tree가 아닌 Self-balancing Tree도 존재합니다.

대표적으로 B Tree가 있는데요.

B Tree는 Binary Tree에서 확장되어 하나의 노드에 여러 개의 데이터를 저장하는 방식을 사용하는 Tree로, 결과적으로 Tree의 height를 줄여 탐색 시간을 줄이는데 목적을 두었습니다.

📃 B-Tree

일반적으로 말하는 B Tree는 B-Tree를 의미합니다.

B-Tree는 모든 leaf 노드들이 같은 depth를 가질 수 있도록 자동으로 균형을 맞추는 self-balancing tree입니다.

보유할 수 있는 자식 노드의 개수를 M이라 하여, 이를 기준으로 M차 B-Tree라고 부르는데요.

이 M차 B Tree는 다음과 같은 특징을 갖습니다.

노드가 보유한 자식 노드의 수는 $ceil(M/2)$ ~ $M$ 개를 만족해야합니다.
- 최대 보유할 수 있는 자식의 수는 사전에 정의한 대로 M개
- Height를 최소화시키기 위해 최소 보유해야만 하는 자식의 수가 M/2개
노드가 보유할 수 있는 key의 개수는 총 $(ceil(M/2)-1)$ ~ $(M - 1)$ 개입니다.
여기서 말하는 key란 데이터의 고유 값을 숫자로 표현한 것으로,
탐색을 원활하게 하기 위해 이진 탐색처럼 부모의 key보다 작은 값은 left로 큰 값은 right로 가도록 정렬됩니다.
- key의 최대 개수가 M-1인 이유 :
  key와 key사이에 자식을 가리키는 포인터가 존재한다는 것을 감안하여,
  key의 수가 M-1일 때 자식이 수가 최대 M개가 될 수 있습니다.
- key의 최소 개수가 M/2-1인 이유 :
  위와 마찬가지로 자식을 최소로 보유하기 위해선 M/2개를 만족해야하기 때문에, 포인터를 감안하여 key의 최소 개수가 M/2-1개가 됩니다.
노드의 key가 x개라면 자식의 수는 x+1개입니다.

위에서도 언급했듯이, key와 key 사이에 포인터가 존재하기 때문에 자식의 수는 자연스럽게 x+1입니다.
ex) pointer — key — pointer — key — … — key — pointer
M차 B tree에서 최소로 보유 가능한 자식의 수는 $M = 2t - 1$ 을 만족하는 $t$ 값입니다.

M = 2t - 1이라는 것이 어떻게 도출되었냐 하면,
맨 위의 특징에서 볼 수 있듯이 최소로 보유 가능한 자식의 수는 $M/2(=t)$ 입니다.

그러면 최대로 보유 가능한 자식의 수는 M개이므로 $2t$ 라고 할 수 있겠죠.
다음으로, 한 노드에서 가지고 있는 key의 수를 $k$ 라 하겠습니다.
그러면 $k$ 는 $k+1$ 개의 자식을 보유할 수 있어야합니다.
즉, $k+1 <= 2t$ 가 성립해야합니다. $k<=2t-1$

그러나, 뭔가 찝찝합니다. $M = 2t-1$ 이라고 했으니, $M$ 은 반드시 홀수가 되야한다는 것이죠.
사실, 처음부터 $M$ 을 홀수로 만들기 위해 $t$ 가 저렇게 설정된 것입니다. $M$ 이 홀수여야만 가운데의 포인터를 통해 노드가 가득찬 상황에서 데이터를 추가할 때 중간 key를 부모로 올릴 수 있기 때문입니다.

그래서 $t$ 도 $ceil(M/2)$ 으로 설정된 이유가 $M$ 이 홀수였기 때문이죠.
예를 들어, M=7인 경우, t = 4이므로 M=2t-1에 의해 M=7이 성립하는 것을 볼 수 있습니다.

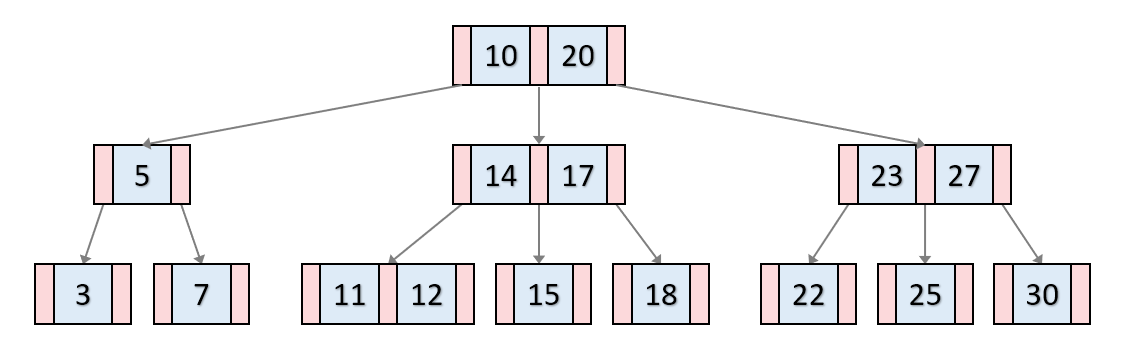
참고 : https://www.quora.com/Why-is-the-maximum-number-of-keys-in-a-B-tree-equal-to-2-t-1-where-t-is-the-minimum-degree

출처 : https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

탐색, 삽입,삭제에 대한 부분은 워낙 잘 정리된 곳이 많아서 링크만 첨부하겠습니다.

시간 복잡도 : $O(logN)$
노드마다 이진 탐색을 통해 포인터를 찾아 자식으로 내려가는 방식이므로,
트리의 높이(h)에 따른 $O(h)$ 가 평균적인 시간복잡도겠지만,

Big O notation은 최악의 상황을 가정해야하므로 h가 $log_MN$ 에 가깝다는 것을 감안했을 때, M=2인 경우라면 트리의 높이가 $log_2N$ 이 되므로 시간복잡도는 $O(logN)$ 입니다.

추가적인 궁금증

RedBlack Tree 대신 B Tree를 인덱스의 자료구조로 사용하는 이유 :
- B Tree가 포인터 접근의 수 측면에서 상당히 유리하기 때문 (Height가 낮으므로)
배열과 B Tree의 비교
- 배열의 장점 : 배열은 포인터를 참조하지 않기 때문에 탐색 속도가 월등히 빠름 O(1)
- 배열의 단점 : 데이터 저장, 삭제 측면에서 B Tree에 비해 압도적으로 불리
인덱스로 해시 테이블을 사용하지 않는 이유 :
- 해시 테이블 내의 데이터는 정렬이 되어있지 않아 부등호 연산이 불가능하기 때문, 인덱스의 특성에 부적합함

📃 B*Tree

B*Tree는 B-Tree에서 노드의 추가적인 생성과 연산을 최소화하기 위해 만들어졌습니다.

B-Tree의 경우 삽입이 될때, 노드가 가득찬 경우 분할을 진행하게 되며 불가피할 경우 노드의 추가적인 생성이 이뤄지게 됩니다.

이에 대한 분할과 생성을 최소화하고자 만들어진 것입니다.

B-Tree와 B*Tree의 차이는 크게 2가지입니다.

최소 자식 수의 변경
- (기존) B-Tree : 보유한 자식 노드의 수는 $ceil(M/2)$ ~ $M$
- B*Tree : 보유한 자식 노드의 수는 $ceil(2M/3)$ ~ $M$
분할 대신 재배치
- (기존) B-Tree : 노드가 가득 차면 분할을 통해 key를 부모로 올리는 작업을 진행
- B*Tree : 노드가 가득 차면 분할 대신 이웃한 형제 노드로 재배치
  ( 재배치 할 수 없는 시점이 되었을 때, 그때 분할을 시행 )

이러한 방식의 변경으로 분할과 생성에 대한 부하를 줄인 것이 B*Tree입니다.

📃 B+Tree

B+Tree는 B-Tree의 탐색을 보다 효율화하기 위해 만들어졌습니다.

B-Tree는 탐색을 위해 노드를 찾아 이동하는 행위를 반복해야합니다.

이 방식은 범위형 쿼리를 작성할 때 단점이 나타납니다.
노드를 따라 내려가는 행위를 범위만큼 반복해야하므로 효율적이지 못하다고 볼 수 있습니다.

이를 개선하고자 B+Tree에서는 leaf 노드에 모든 데이터(key)를 저장하고 모든 leaf 노드를 linked list로 연결해두었습니다.

B+Tree의 간략 설명

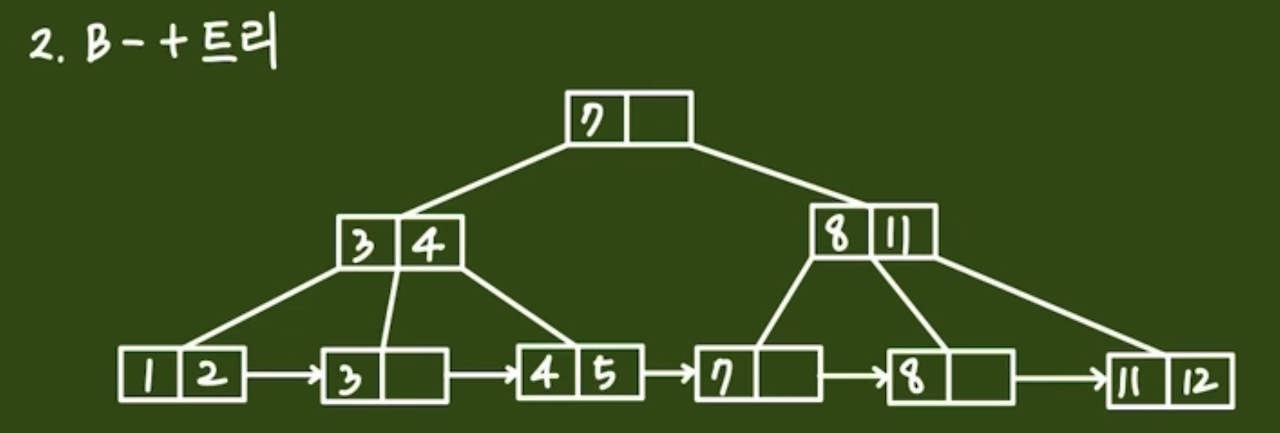
출처 : https://engineerinsight.tistory.com/336

B+Tree에서는 노드를 크게 2가지로 분류합니다.

데이터 노드 : leaf 노드
인덱스 노드(internal 노드) : leaf 노드가 아닌 노드

데이터 노드인 leaf 노드에는 실제로 key값과 데이터(value)가 모두 존재하고,
인덱스 노드는 해당 데이터를 찾기 위한 key값과 포인터들만 존재하는 것이죠.

데이터 노드에 모든 key값이 존재해야하기 때문에 인덱스 노드의 key값들도 전부 데이터 노드에서 등장합니다.

원하는 데이터를 찾기 위해선 인덱스 노드를 통해 leaf 노드까지 내려가야합니다.

B-Tree와 B+Tree의 비교

탐색
- root 노드에서 시작해서 key값을 비교해가며 내려가는 방식은 동일
- B-Tree : 중간에 internal 노드에 해당 key값을 찾으면 종료
- B+Tree : leaf 노드까지 내려가야만 종료
삽입, 삭제
- 동일하게 분열 및 노드 생성을 실시합니다.
메모리
- B-Tree : 모든 노드에 key, value, pointer를 보유
- B+Tree : value는 leaf 노드에만 존재하므로, 인덱스 노드의 메모리에 더 많은 key값을 수용할 수 있음 (height가 낮아짐)
범위 탐색
- B-Tree : 일일히 범위 내의 모든 값을 찾기 위해 Root -> Leaf까지 내려가는 행위를 여러번 반복해야함
- B+Tree : leaf 노드가 linked list로 연결되어있으므로 최소 혹은 최대값을 찾은 후 순차탐색을 진행하면 됨

B+Tree가 인덱스로 적합한 이유

인덱스 노드에 value를 저장하지 않음으로써, key값을 더 많이 갖을 수 있게되고 이는 M의 증가, 즉, 트리의 높이가 낮아지는데 영향을 줍니다.

트리의 높이가 왜 중요하냐면?

인메모리에 올려두고 사용할 때는 문제되지 않지만, 데이터의 양이 매우 큰 경우 디스크를 사용해야합니다.

하드디스크에 접근해 데이터를 불러오는 시간은 인메모리에 비해 매우 크기 때문에 최대한 디스크 접근 횟수를 줄이는 것이 중요합니다.

따라서, 디스크 접근횟수를 줄인다는 것은 포인터의 접근 횟수를 줄이는 것이고, 이는 트리의 높이를 줄인다는 것과 동일합니다.

또한, select * from table과 같이 특정 테이블 풀스캔을 하는 경우
B+tree는 linked list를 통해 선형탐색을 진행하면 되기 때문에 상대적으로 매우 빠를 수 밖에 없습니다.