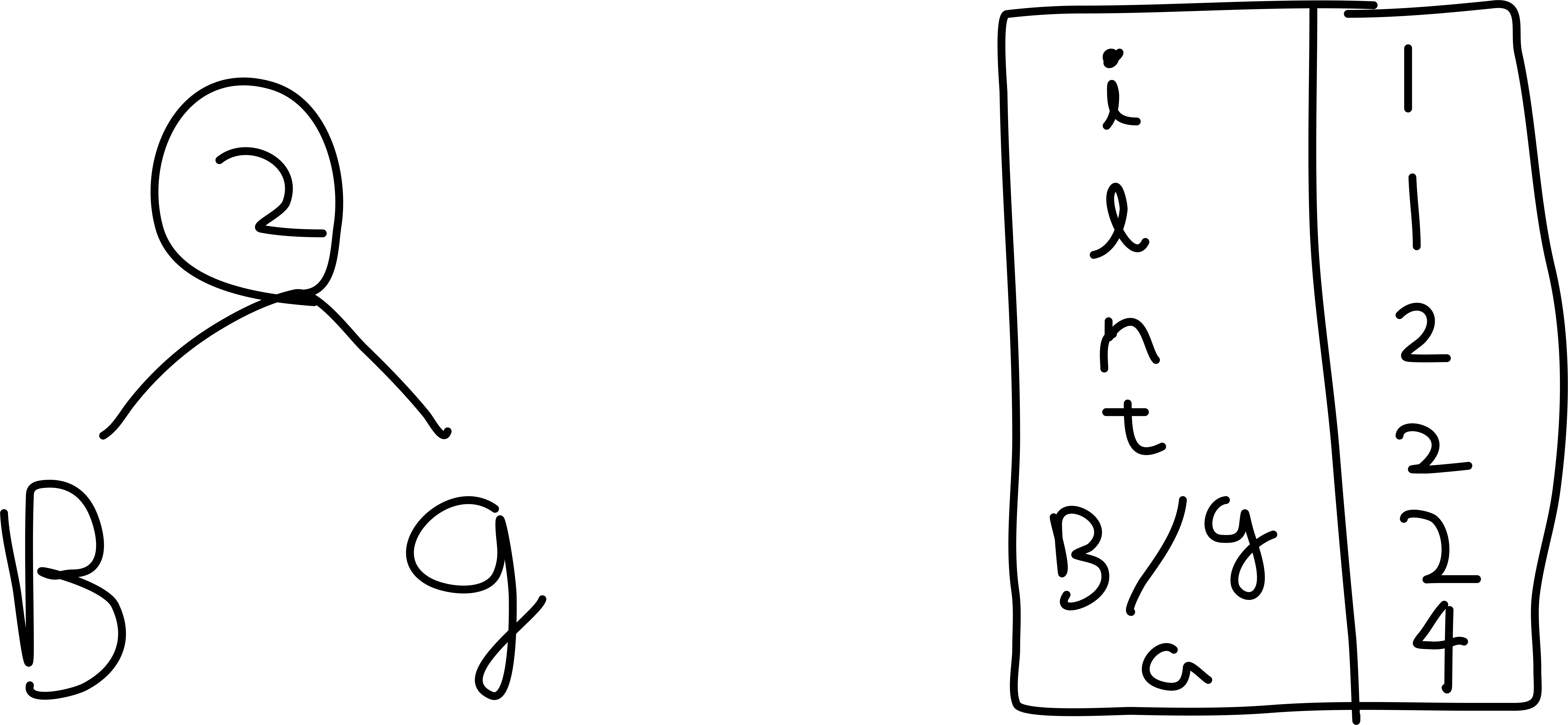들어가면서..
url 주소의 최대 길이를 생각보신 적 있나요??
저도 이번에 찾아보면서 알게 됐는데, 브라우저/버전 별로 차이가 꽤 많이 있었습니다.
이미지를 클릭하면, 관련 stackoverflow 게시글로 이동합니다. :)
(* 이걸 직접 실험해서 알아보는 사람들이 있네요..)
Internet Explore 가 대략 2,000자 ~ 3,000 자 정도로 허용범위가 제일 적네요💦
주소창에 데이터를 저장하고 싶은 제 입장에서야 그 길이를 많이 허용해주면 좋겠지만, url 을 이용해 server 공격이 이뤄지기도 한다니까 browser vendor 입장에선 충분히 제한할 수 있는 부분이겠죠?..
그렇다면, 허용된 길이를 넘어서 url에 많은 데이터를 저장할 경우 어떻게 될까요??
위의 사이트에서 보니, Chorm 에서 허용되는 최대 url 길이는 대략 32,000 자인 것 같습니다. 이전 1편에서 작성했던 것과 비슷한 코드로, Chorm 브라우저에서 useSearchParam 을 이용해 url 길이를 계~속 증가시켜봤습니다.
사실 이정도로도 충분히 많은 데이터를 저장했습니다만, 그래도 브라우저마다 제한하는 길이도 다르니, 모든 유저에게 동일한 서비스가 제공되는 건 힘들 것 같습니다.
이를 개선할 수 있는 방법 중 하나로 저는 문자열 압축을 떠올렸어요.! 지난 편에 적었던 것처럼 url 에 저장된 것은 모두 string 형식입니다. 문자열 압축 알고리즘을 이용한다면, 지금보다 훨씬 더 많은 데이터를 효과적으로 저장할 수 있지 않을까요?
➕ 추가적으로 base64 의 단점을 보안하기 위해서라도 이 과정이 꼭 필요합니다.!이번 포스트에서는 base64 의 encoding 방법과 문자열 압축 알고리즘에 대해 다뤄보겠습니다.
base64
개념
0과 1로 이뤄진 binary data 를 ASCII 체계의 문자열로 변환하는 인코딩 방식입니다. 6비트 (2^6 = 64) 단위로 하나의 문자를 만들기 때문에, base'64' 라고 불립니다.
ASCII code 중 어떤 것을 입력으로 받더라도,
encoding 결과로 출력되는 건 64개의 문자 집합 중 하나입니다 :)왜 사용하나요?
binary data 로 이뤄진 리소스(이미지 등) 에 대해, 오류없이 데이터 통신을 하기위해 사용합니다.
🤔: 그냥 binary data 자체로 보내면 안되나?
👆:
- binary data 그대로 전송하는 표준 프로토콜 또한 존재합니다.
- 하지만 텍스트 기반의 data 로 통신해야 하는 경우, 문자열 형태로 변형 해야합니다.
- http, https 등의 프로토콜을 이용해 html(문서) 을 전송하는 경우,
그 안에 포함해야할 리소스의 data 를 변형하여 문서에 포함시키는 것이 대표적인 예입니다.동작원리
하나의 예시로 변화과정을 따라가 보겠습니다.
별로 어렵지 않습니다.🙂
1. binary data 로 전환
"abc" 라는 문자열에 대해, ASCII table 을 통해 이진수를 출력해보면 다음과 같습니다.
| character | ASCII code | binary |
|---|---|---|
| a | 97 | 01100001 |
| b | 98 | 01100010 |
| c | 99 | 01100011 |
"abc" -> 01100001 01100010 01100011
2. 6bit 씩 그룹화
base64 encoding 을 거치면, 8bit 당 하나의 문자를 구성했던 기존과 달리 6 bit 당 하나의 문자로로 매핑된 결과를 얻습니다.
"abc" -> 011000010110001001100011 -> 011000 010110 001001 100011
이에 대한 ASCII code 는 아래와 같습니다.
| 6bit binary | ASCII code |
|---|---|
| 011000 | 24 |
| 010110 | 22 |
| 001001 | 9 |
| 100011 | 35 |
"abc" -> 011000010110001001100011 -> 011000 010110 001001 100011 -> 24 22 9 35
3. Base64 Table Mapping
위의 테이블을 참고해, mapping 하면 encoding 결과를 얻을 수 있습니다.
| 6bit binary | ASCII code | Base64 mapping |
|---|---|---|
| 011000 | 24 | Y |
| 010110 | 22 | W |
| 001001 | 9 | J |
| 100011 | 35 | j |
"abc" -> 011000010110001001100011 -> 011000 010110 001001 100011 -> 24 22 9 35 -> "YWJj"
"abc" 의 base64 encoding 결과는 "YWJj" 입니다.!
(* decoiding 은 encodig 을 역순입니다!)
단점
위의 예시에서 보면 알 수 있듯이, 8비트씩 나눠 하나의 문자로 인식하던 것을 6비트씩 나누게 되었으므로, 데이터 수가 증가하는 이슈가 발생합니다. 관련 포스트를 찾아보면 "33% 증가" 라는 말이 눈에 띄는데 그 이유가 여기에 있습니다.
🤔: 굳이 왜 6bit 씩 끊어 읽는가?
👆:
- 이는 ASCII 문자의 표현에 문제가 없도록 하기 위한 선택사항일 뿐입니다.
- ASCII 체계에서 한 문자를 표현하기 위해 7bit 면 충분합니다.
- 8bit 데이터를 6bit 씩 끊게 되므로, 가능한 모든 조합을 ASCII 문자로 표현 가능합니다. How then?
다시 "주소창에서의 데이터 관리" 이야기로 돌아갑시다.
주소창에 원본 데이터가 그대로 노출되는 것을 방지하기 위해 기껏 encoding 과정을 추가했더니, 원본보다 저장해야할 크기가 더 커지는 문제가 발생했습니다.
데이터를 더 많이 저장하기 위해 고려할 수 있는 옵션 중 하나는, encoding 된 문자열을 압축시키는 것입니다.
열심히 찾아본 결과, 문자열을 압축할 수 있는 방법 중 널리 사용되는 두 개의 알고리즘을 발견할 수 있었어요. 이 후부터는 해당 알고리즘의 동작원리에 대해 찾아보고 정리한 내용입니다. 🙂
Huffman Coding
7bit 만 있으면 ASCII 체계에서 모든 문자를 표현할 수 있습니다.
A = 0100001
B = 0100002
.
.모든 { 영문 + 숫자 + 어떤(?) 특수기호} 에 bit를 부여합니다. 그 중에는 잘 사용하지 않는 특수문자도 마찬가지입니다.
Huffman code 에서는 특정 파일 혹은 데이터 집단에서 사용한 문자만을 대상으로 bit 를 부여합니다. 추가적으로, 각 문자의 빈도수를 계산해서 많이 사용하는 문자에는 적은 비트가 할당하도록 설계했어요.
동작예시
간단한 예시를 보겠습니다.
특정 파일을 열였을 때, 다음 문자열이 기록되어있다고 가정할게요.!
"ttalgiBanana"
길이가 12인 문자열에 대해, ASCII 체계에선 각 문자당 7bit 면 표현 가능합니다.
하지만, 컴퓨터 상에서 이를 관리하기 위해 각 문자마다 하나의 비트를 더 추가해 8bit 로 할당합니다.
't': 01110100
't': 01110100
'a': 01100001
'l': 01101100
'g': 01100111
'i': 01101001
'B': 01000010
'a': 01100001
'n': 01101110
'a': 01100001
'n': 01101110
'a': 01100001
=> 01110100 01110100 01100001 01101100
01100111 01101001 01000010 01100001
01101110 01100001 01101110 01100001딱 봐도 문자 하나하나 많은 bit 가 할당된 거 같아요.!
중복된 값도 많이 보이는, 각 위치에서 당당히 8 자리씩 차지하고 있네요 👍
이제 Huffman Coding 으로 이를 압축해보겠습니다.
1. 빈도 분석
첫번째 과정은 각 문자에 대한 빈도수를 먼저 계산하는 것입니다.
| 문자 | 빈도수 |
|---|---|
| B | 1 |
| g | 1 |
| i | 1 |
| l | 1 |
| t | 2 |
| n | 2 |
| a | 4 |
2. Huffman tree 생성
이제 빈도수 를 기반으로 트리를 생성해요. 빈도가 가장 적은 두 문자(노드) 에 대해, 부모노드를 만들면 됩니다. 부모 노드에는 각 자식의 빈도수를 합한 값을 할당해요. 저도 다음의 규칙을 가지고 tree 를 만들어 봤어요 :)
- 빈도수가 적다면 오른쪽 노드가 됩니다.
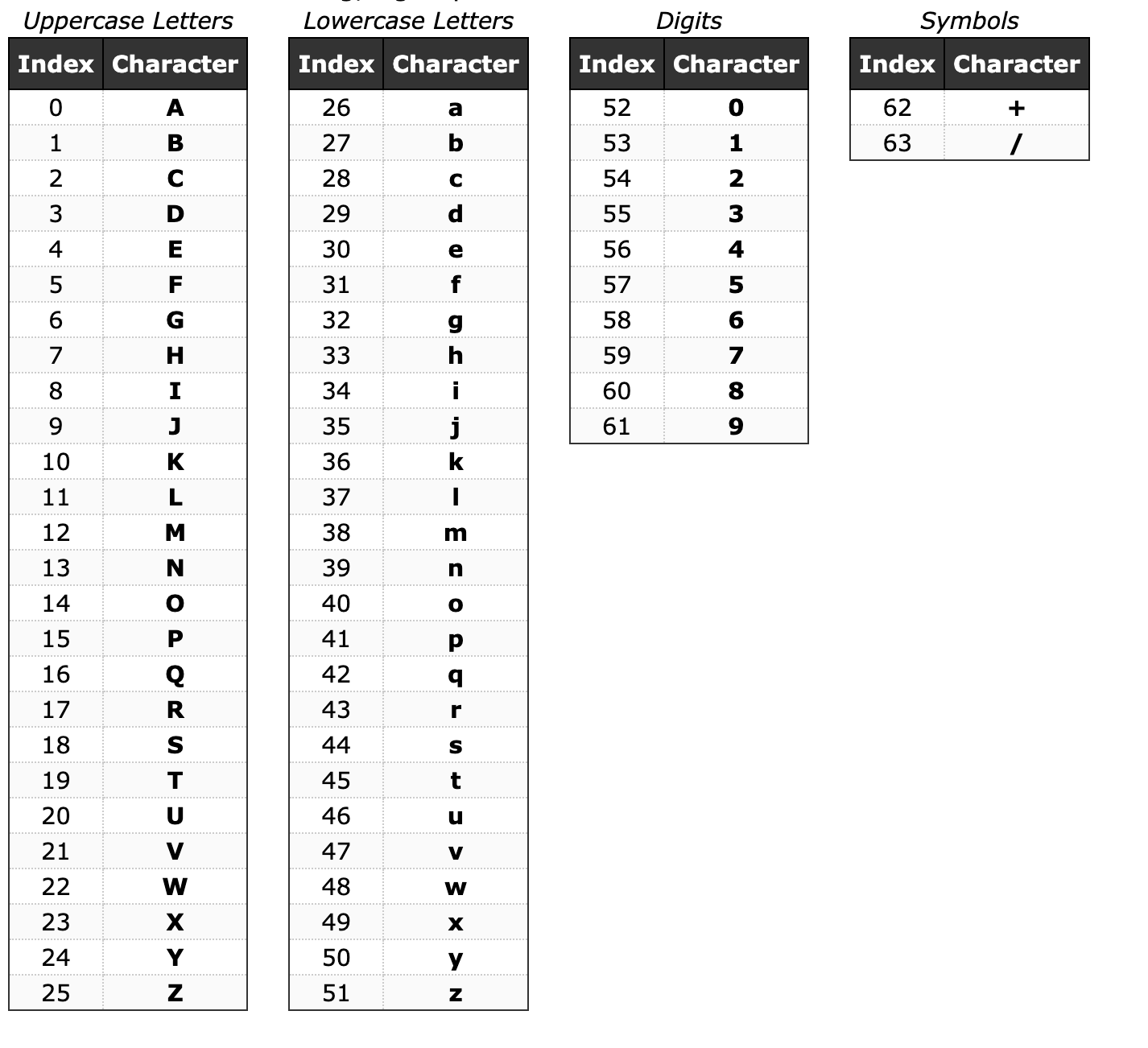
- 알파벳 순서가 앞선다면 오른쪽 노드가 됩니다. (소문자가 대문자보다 앞선다고 가정합니다.)[1] 먼저, 빈도수가 가장 적은 'B' 노드와 'g' 노드가 트리를 이룹니다.
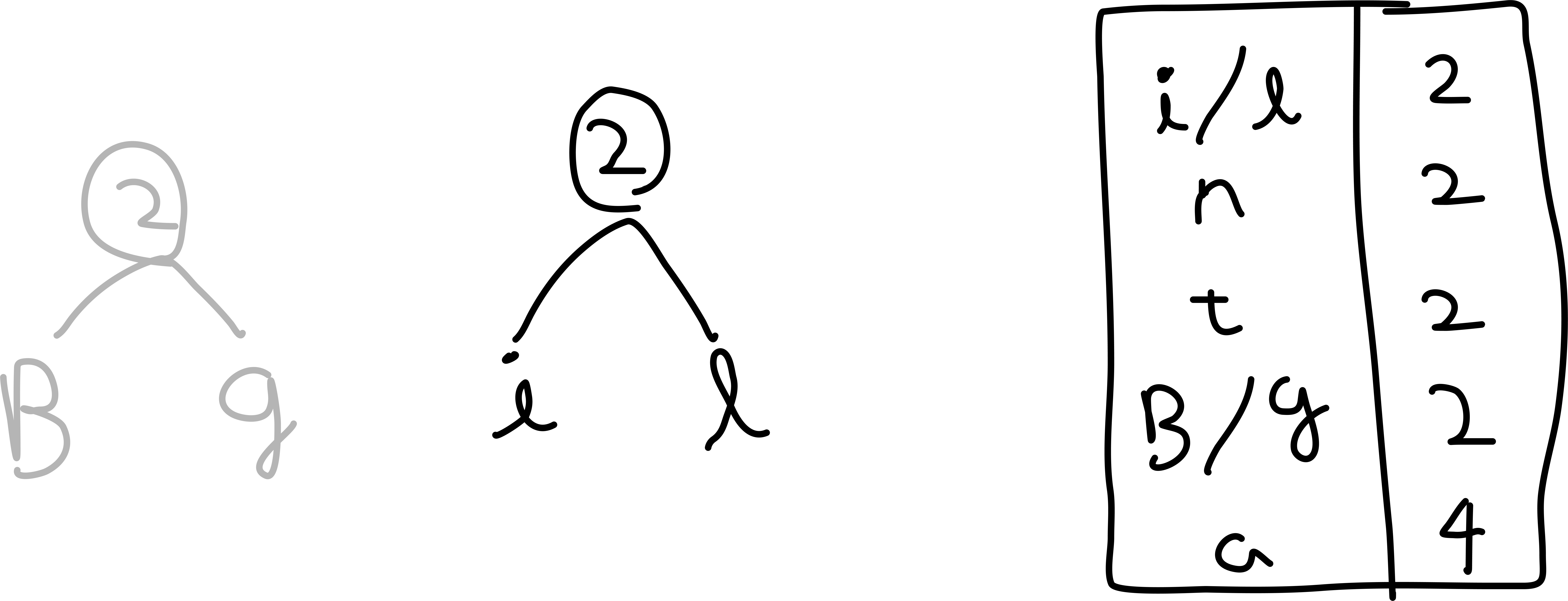
[2] 그 다음은, 'i' 노드와 'l' 노드 입니다. 'i' 과 'l' 로 만든 트리와 'n' 은 빈도수가 같지만, 알파벳 기준으로 'i' 이 'n' 보다 앞서므로 우선순위가 높습니다.
[3] 'i', 'l' 트리 + 'n' 노드
[4] 't' 노드 + 'B','g' 트리
[5] 'a' 노드 + 'B','g','t' 트리
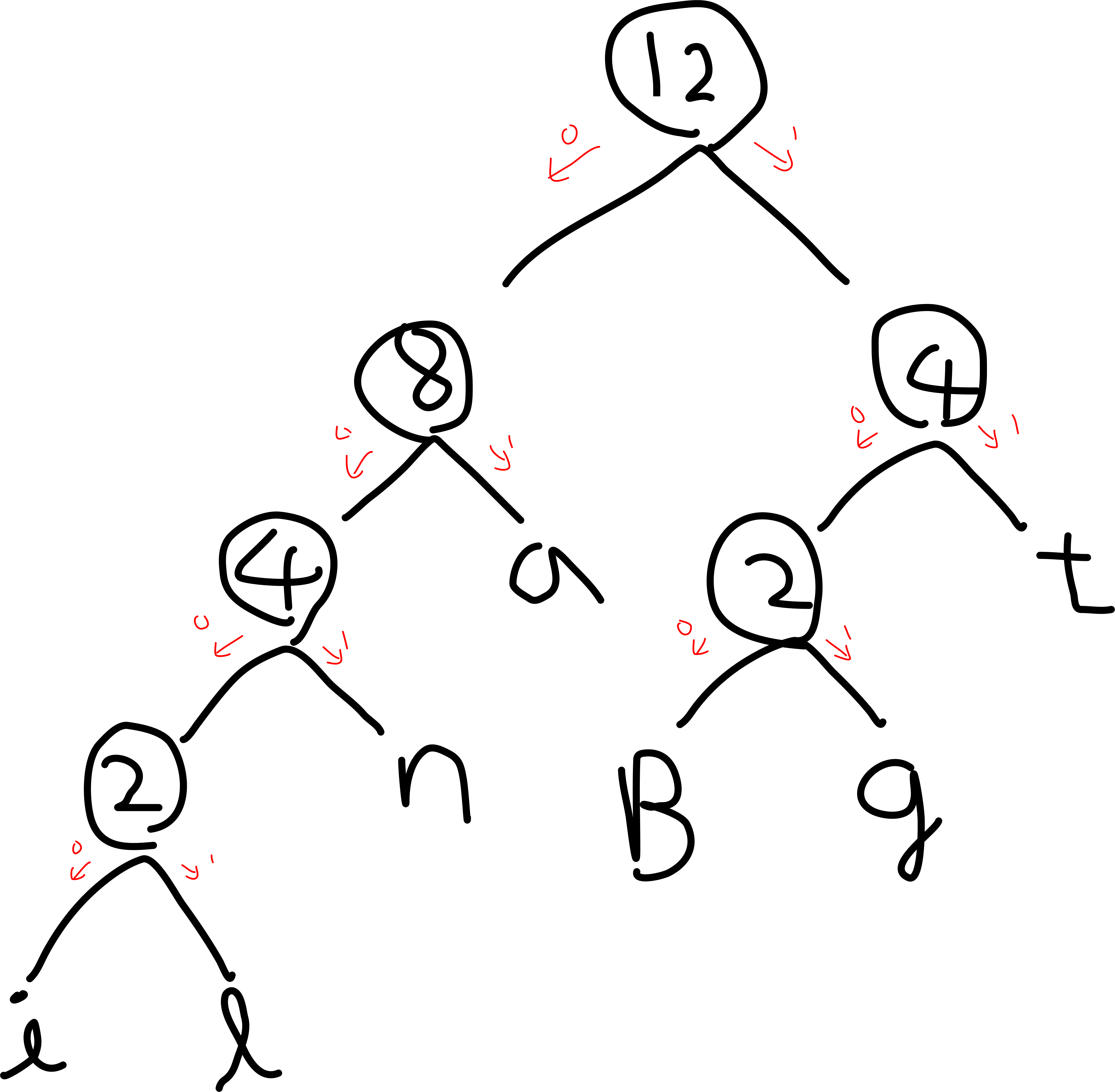
[6] 모든 노드를 포함한 트리를 완성했습니다.!
3. bit 할당
[6] 이미지를 참고해서, tree 의 root 부터 한 depth 씩 내려가봅시다. 왼쪽으로 내려가면 0 을, 오른쪽으로 내려가면 1을 하나씩 붙혀주면 됩니다. 예를 들어 'a' 의 경우, root 에서 왼쪽 -> 오른쪽 순으로 내려왔으니 01 이 할당됩니다. 다른 것도 마찬가지로 구해보면,,
// 32 bit
't': 10
't': 10
'a': 01
'l': 0001
'g': 101
'i': 0000
'B': 100
'a': 01
'n': 001
'a': 01
'n': 001
'a': 01
=> 10 10 01 0001 101 0000 100 01 001 01 001 01기본적으로 문자 하나에 할당된 비트수가 눈에 띄게 줄어들었습니다.
원본 크기의 대략 33% 수준입니다.
/*압축 전*/
01110100 01110100 01100001 01101100 01100111 01101001
01000010 01100001 01101110 01100001 01101110 01100001
/*압축 후*/
10 10 01 0001 101 0000 100 01 001 01 001 01추가적으로 빈도수가 가장 많았던 a (3),n (2),t (2) 에 대해선 더 적은 비트가 주어졌어요.
문자열이 더 길고, 반복되는 문자가 많을수록 그 효과가 더 좋아지겠죠? 👍
적용 & 개선 효과
Lumpel-ZIv (LZ) Coding
사실 저의 사이드 프로젝트에서 url 길이와 관련된 문제가 발생하고, 이를 해결하기 위해,
lz-string이라는 라이브러리 설치 / 사용하여 문제를 개선하였습니다. 근데 이와 관련된 알고리즘의 버전 및 후속 연구가 엄~청 많아요.🥲LZ77, LZR, LZSS, LSH, LZ78, LZW, LZJ 등등등...음,, 일단 제가 사용했던 라이브러리에서 압축을 구현한 알고리즘을 정리하겠습니다.
🎯 타겟은 LZW 입니다.! 🔥
"Huffman 압축" 에서는 bit 단위에서, tree를 만들어 문자 하나하나를 짧은 코드로 대체하였습니다.
반면 "LZW 압축" 의 경우, 문자 하나하나가 아니라 연이어 등장하는 문자열을 단축된 코드로 대체합니다. 또 하나의 차이점은 tree 대신, dictionary(map, key-value 쌍을 가지는 자료구조) 를 만들어 가는 것이죠. (이후부터는 "dictionary" 를 사전이라고 하겠습니다.)
🙃 참고 (넘어 가셔도 좋습니다.)
n-gram 이라는 개념에 대해 쉽고 짧게 설명드리겠습니다.
길이가 1인 문자열, unigram 길이가 2인 문자열, bigram 길이가 3인 문자열, trigram 길이가 4인 문자열, 4-gram 길이가 5인 문자열, 5-gram . . .앞으로 사전을 갱신하는 과정을 따라갈 예정입니다. lzw 옵션으로 사전에 등록할 수 있는 최대 문자열을 지정할 수 있는데, 이 설정을 n-gram 이라고 표현합니다.! 👍
동작예시
chocochocochococho
위의 문자열을 압축하는 과정을 따라가겠습니다.
'c': 01100011
'h': 01101000
'o': 01101111
'c': 01100011
'o': 01101111
'c': 01100011
'h': 01101000
'o': 01101111
'c': 01100011
'o': 01101111
'c': 01100011
'h': 01101000
'o': 01101111
'c': 01100011
'o': 01101111
'c': 01100011
'h': 01101000
'o': 01101111
=> 01100011 01101000 01101111 01100011 01101111 01100011 01101000 01101111 01100011 01101111 01100011 01101000 01101111 01100011 01101111 01100011 01101000 01101111위에서 말씀드렸다시피, ASCII code 는 7bit 로 전부 표현할 수 있습니다.
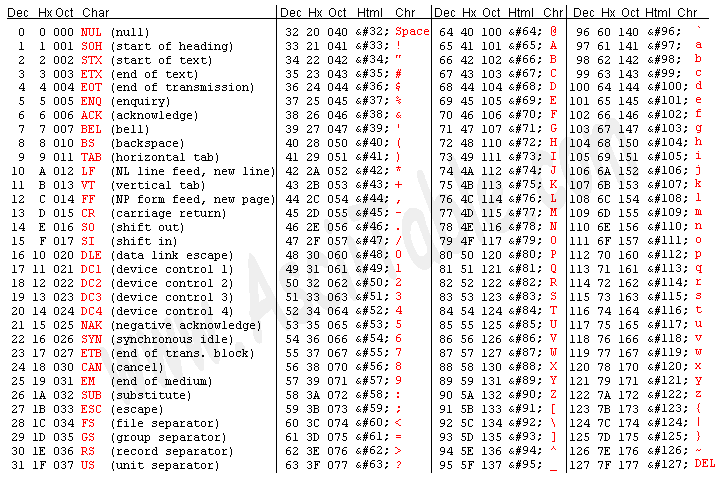
* 아래 이미지를 보면, 0 ~ 127 (2⁷ - 1) 까지 매핑되어 있습니다. 🙂
사전(dictionary) 에는 ASCII code 를 다음과 같이 미리 포함해두겠습니다.
| character | code |
|---|---|
| NUL | 0 |
| ... | ... |
| A | 65 |
| B | 66 |
| C | 67 |
| D | 68 |
| ... | ... |
| } | 125 |
| ~ | 126 |
| DEL | 127 |
이제 chocochocochococho 의 한글자 씩 읽어가면서, 사전에 조회 후 등록된 값이 없을 경우에만 그것을 갱신하는 과정을 반복하면 됩니다.
사전에 이미 있는 값이라면, 그 다음 문자 하나를 더 가져와 함께 조회합니다.
🔥 진행상황 : c hocochocochococho
📀 code변환 : -첫번째로 읽을 문자는
c입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('c' 의 code 는 99 입니다.)ASCII table 에 있는 문자는 이미 다 포함해 두었습니다.
이럴 경우, 이 다음에 읽을 문자와 합쳐서 다시 사전에 조회합니다.
🔥 진행상황 : ch ocochocochococho
📀 code변환 : -그 뒤에 등장한 문자는
h입니다.
남아있던c와 합쳐ch를 조회합니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
ch에 가장 마지막 code 의 다음 번호, 128 을 주고 사전에 등록합니다.
character code ... ... ~ 126 DEL 127 ch 128
🔥 진행상황 : ch o cochocochococho
📀 code변환 : 128그 뒤에 등장한 문자는
o입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('o' 의 code 는 111 입니다.)
🔥 진행상황 : ch oc ochocochococho
📀 code변환 : 128그 뒤에 등장한 문자는
c입니다.
남아있던o와 합쳐oc를 조회합니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
oc의 code 는 129 입니다.
character code ... ... DEL 127 ch 128 oc 129
🔥 진행상황 : choc o chocochococho
📀 code변환 : 128 129그 뒤에 등장한 문자는
o입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('o' 의 code 는 111 입니다.)
🔥 진행상황 : choc oc hocochococho
📀 code변환 : 128 129그 뒤에 등장한 문자는
c입니다.
남아있던o와 합쳐oc를 조회합니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('oc' 의 code 는 129 입니다.)
🔥 진행상황 : choc och ocochococho
📀 code변환 : 128 129그 뒤에 등장한 문자는
h입니다.
남아있던oc와 합쳐och를 조회합니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
och의 code 는 130 입니다.
character code ... ... ch 128 oc 129 och 130
🔥 진행상황 : chococh o cochococho
📀 code변환 : 128 129 130그 뒤에 등장한 문자는
o입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('o' 의 code 는 111 입니다.)
🔥 진행상황 : chococh oc ochococho
📀 code변환 : 128 129 130그 뒤에 등장한 문자는
c입니다.
남아있던o와 합쳐oc를 조회합니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('oc' 의 code 는 129 입니다.)
🔥 진행상황 : chococh oco chococho
📀 code변환 : 128 129 130그 뒤에 등장한 문자는
oco입니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
oco의 code 는 131 입니다.
character code ... ... ch 128 oc 129 och 130 oco 131
🔥 진행상황 : chocochoco c hococho
📀 code변환 : 128 129 130 131그 뒤에 등장한 문자는
c입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('c' 의 code 는 99 입니다.)
🔥 진행상황 : chocochoco ch ococho
📀 code변환 : 128 129 130 131확인할 문자는
ch입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('ch' 의 code 는 128 입니다.)
🔥 진행상황 : chocochoco cho cocho
📀 code변환 : 128 129 130 131확인할 문자는
cho입니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
cho의 code 는 132 입니다.
character code ... ... ch 128 oc 129 och 130 oco 131 cho 132
🔥 진행상황 : chocochococho c ocho
📀 code변환 : 128 129 130 131 132확인할 문자는
o입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('o' 의 code 는 🔥 입니다.)
🔥 진행상황 : chocochococho co cho
📀 code변환 : 128 129 130 131 132확인할 문자는
co입니다.👆 사전에 있는 값인가? . . . ❌ 없습니다.
co의 code 는 133 입니다.
character code ... ... ch 128 oc 129 och 130 oco 131 cho 132 co 133
🔥 진행상황 : chocochocochoco c ho
📀 code변환 : 128 129 130 131 132 133확인할 문자는
c입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('c' 의 code 는 99 입니다.)
🔥 진행상황 : chocochocochoco ch o
📀 code변환 : 128 129 130 131 132 133확인할 문자는
ch입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('ch' 의 code 는 128 입니다.)
🔥 진행상황 : chocochocochoco cho
📀 code변환 : 128 129 130 131 132 133확인할 문자는
cho입니다.👆 사전에 있는 값인가? . . . ✅ 있습니다. ('cho' 의 code 는 132 입니다.)
그리하여, 최종적으로 변환된 코드는 다음과 같습니다.
128 129 130 131 132 133 132이를 이진수로 변화하여 원본과 비교를 해보면,,
/*압축 전*/
01110100 01110100 01100001 01101100
01100111 01101001 01000010 01100001
01101110 01100001 01101110 01100001
/*압축 후*/
10000000 10000001 10000010 10000011 10000100 10000101 10000100대략 60% 압축효과가 있었네요.
마치며
두 알고리즘의 예시가 다르기도 했고, 입력 문자열에 따라 적합한 알고리즘이 매번 달라질 수 있습니다. 하지만 Huffman Coding, LZW Coding 의 차이점이 있는데, 전자의 경우 트리를 위해 파일 전체를 한번 순회해야하지만 LZW Coding 은 한 byte 씩 읽어가면 압축을 실행할 수 있습니다. 물론 메모리 효율의 이슈가 많이 제기되는 모양인데, 이를 최적화한 버전이 계속 나온다고 합니다. 🫠
알고리즘에 대해 포스트를 작성하는게 처음이라, 생각보다 게시글이 많이 길어졌습니다.. (압축 방법에 대해 이해하는 것부터 쉽지 않았어요..)
분량 상의 문제로, 제 프로젝트에 적용하여 효과가 개선된 이야기는 다음 편에 다루도록 하겠습니다.