[문제설명]
가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.
- 타일을 가로로 배치 하는 경우
- 타일을 세로로 배치 하는 경우
예를들어서 n이 7인 직사각형은 다음과 같이 채울 수 있습니다.
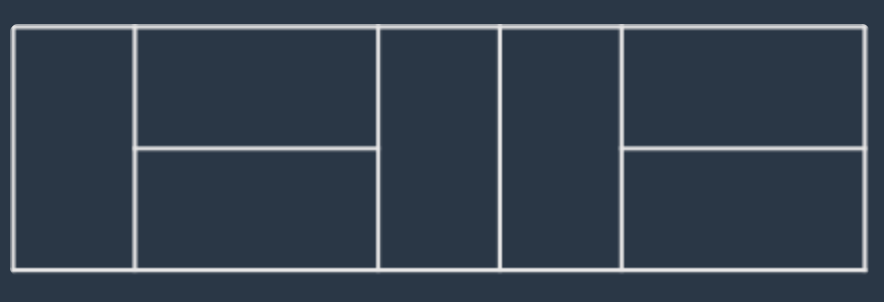
직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.
[제한 조건]
가로의 길이 n은 60,000이하의 자연수 입니다.
경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.
[나의 풀이 (1차)]
// 가로의 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일
// 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우자
// 즉 1과 2를 조합해서 n을 만들자.
class Solution {
public static int cnt = 0;
public int solution(int n) {
int answer = 0;
dfs(0, n);
return cnt;
}
public void dfs(int sum, int n) {
if (sum == n) {
cnt++;
return;
} else if (sum > n) {
return;
} else {
dfs(sum + 1, n);
dfs(sum + 2, n);
}
}
}어차피 바닥의 세로의 길이는 2로 고정되어있고, 또한 타일의 경우 2x1로 크기가 고정되어 있으므로, 단순하게 가로의 길이만 체크해주기만 하면 될 것 같았다.
즉, 가로의 길이인 2와 세로의 길이인 1을 이용해서 n을 만들어주기만 하면 문제는 쉽게 마무리 되었다.
따라서, 처음 접근방법으로는 dfs를 떠올렸다. 재귀적으로 1과 2를 더하다가 그 합이 n과 같아지면 cnt를 증가시키는 방식으로 접근하였다.
그러나...
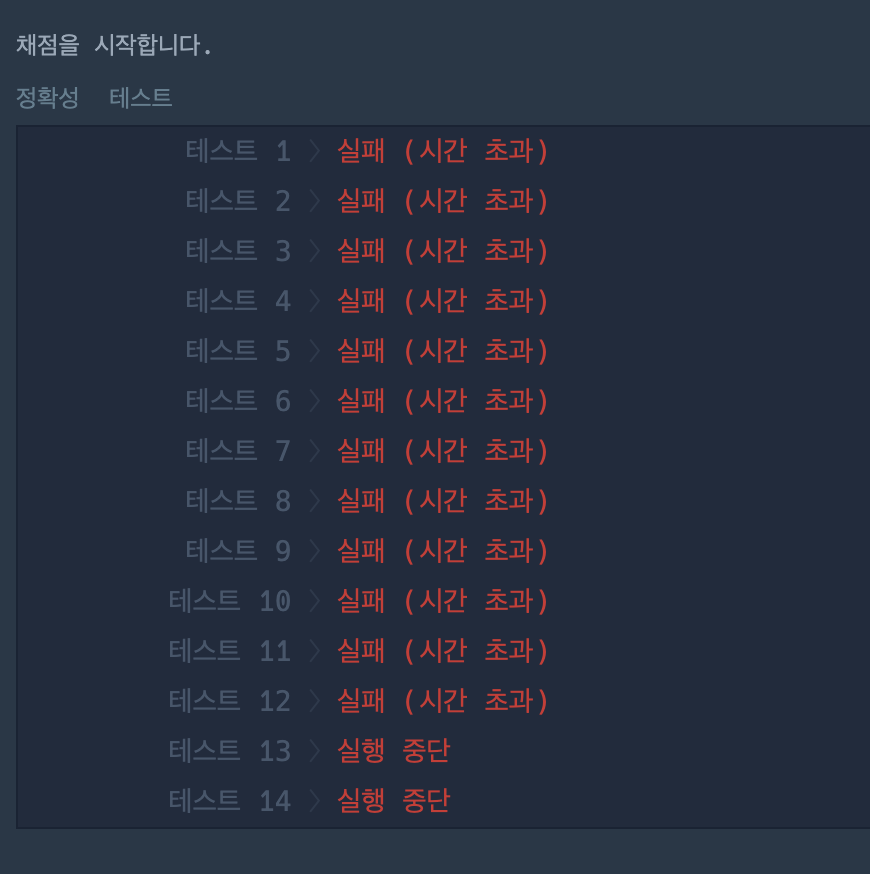
무수한 시간초과와 함께 통과하지 못하였다.😇
모든게 다 시간초과가 뜨는 것을 보니 아무리 dfs를 최적화 시켜도 답이 없어 보였다.
따라서 다른 풀이법을 생각해보았다.
[나의 풀이 (2차)]
// 피보나치 수열을 이룬다.
class Solution {
public int solution(int n) {
int answer = 0;
int[] dp = new int[n];
dp[0] = 1;
dp[1] = 2;
for (int i = 2; i < n; i++) {
dp[i] = dp[i-2] + dp[i-1];
dp[i] %= 1000000007;
}
return dp[n-1];
}
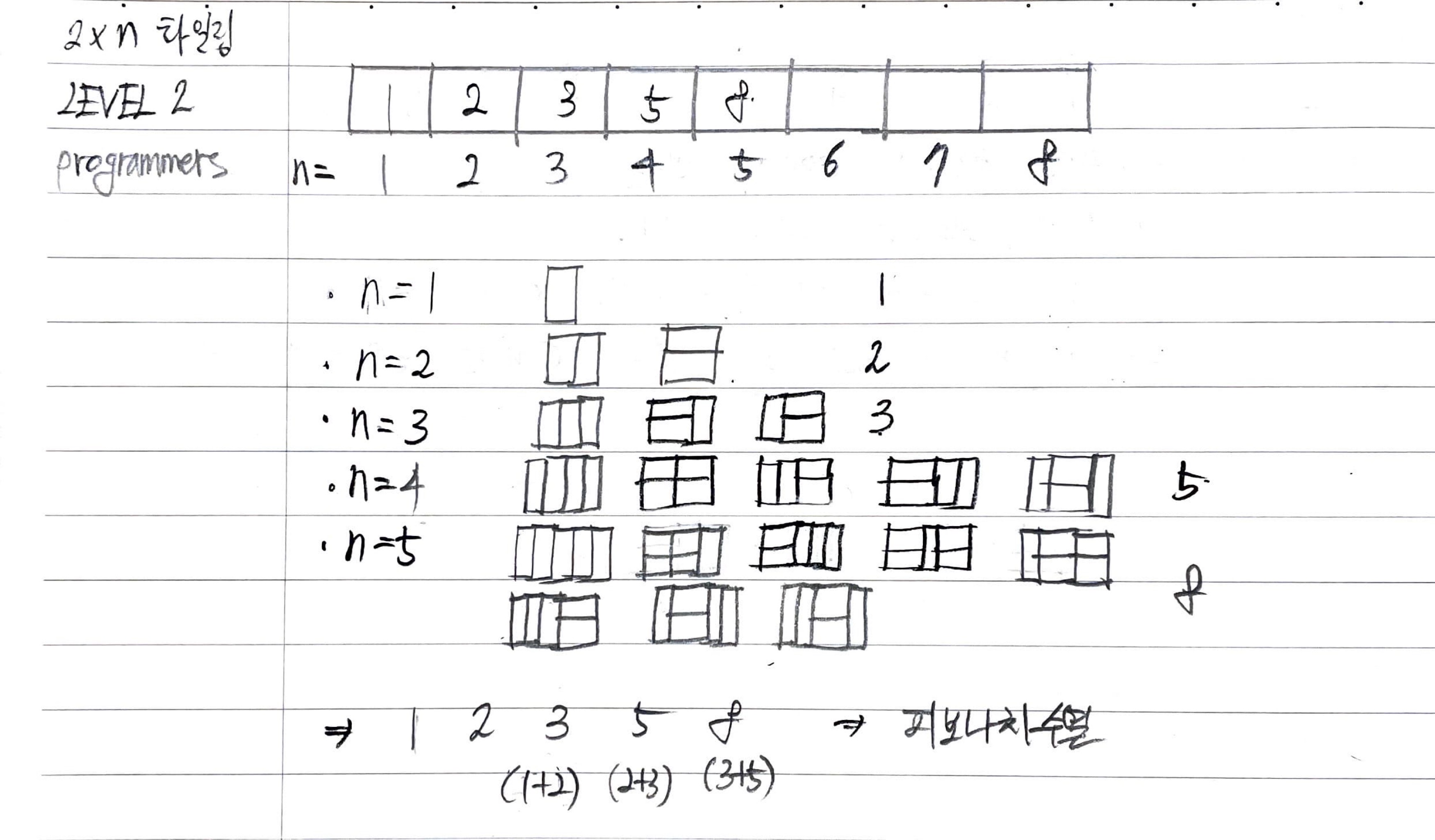
}(직접 손으로 해봄..)
하나하나씩 손으로 그려가면서 규칙을 찾아보려구 했는데..
역시나 규칙이 있었다...😓 (미리 해볼걸...)
피보나치 수열을 이룬다는 것을 발견하였고, 이걸 안 순간 문제의 난이도는 급감하기 시작했다.
동적계획법의 메모이제이션을 이용하여 풀이를 완료하였다.
이때, 배열의 각 원소를 계산할때마다 1,000,000,007를 나누어주어야 한다. 왜?? 값의 오버플로를 방지하기 위해서이다. 오버플로 나면 값이 이상해 지니까 그 전에 미리미리 매번 나눠서 숫자를 작게 유지하는것이다.
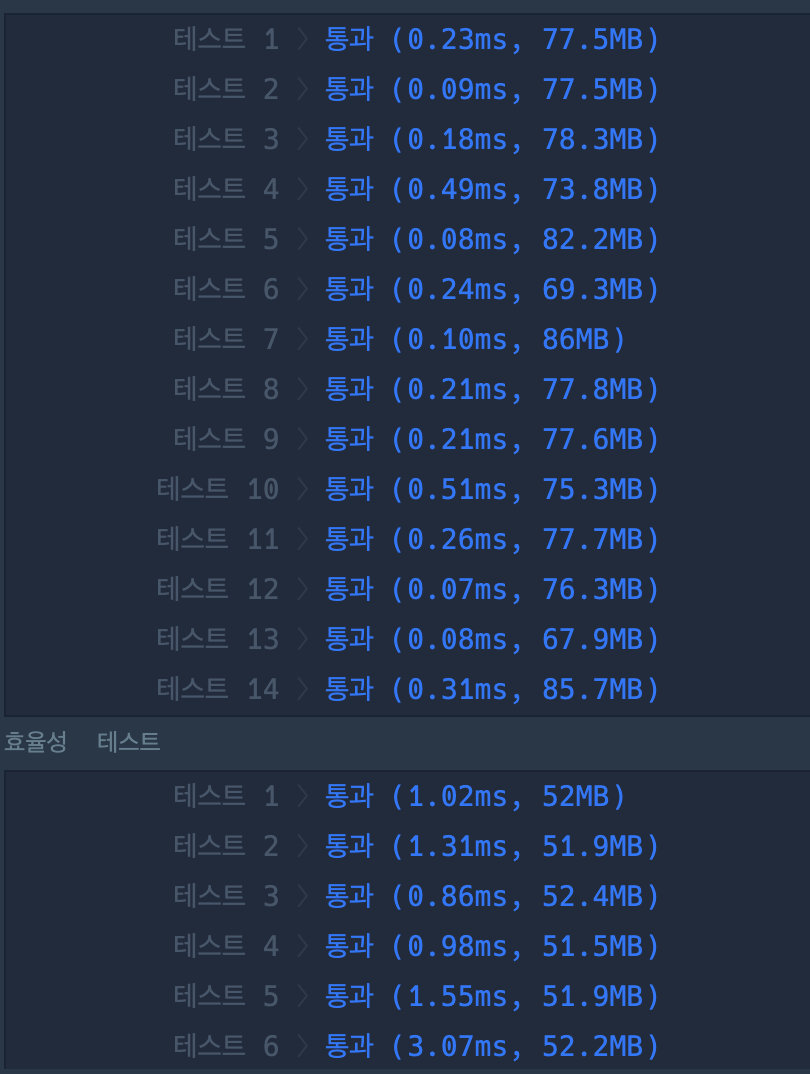
아래는 채점결과이다.