1. CCW 란

• CCW (Counter Clock Wise, 원래 의미는 시계 반대방향) 는 3개의 점 r, p, q가 있을때 벡터 rp를 기준으로 점 q가 어느 위치(왼쪽, 같은 직선, 오른쪽)에 있는지를 판별하는 방법입니다.
• 벡터의 외적입니다.
• 외적은 교환법칙이 성립하지 않습니다. AB 와 BA가 같지 않습니다.
• 기하 알고리즘의 가장 기본 개념입니다.
• 보통 결과물은 다음과 같이 작성합니다.
• 1) 왼쪽에 있을때, 1
• 2) 같은 직선상에 있을때, 0
• 3) 오른쪽에 있을때, -1

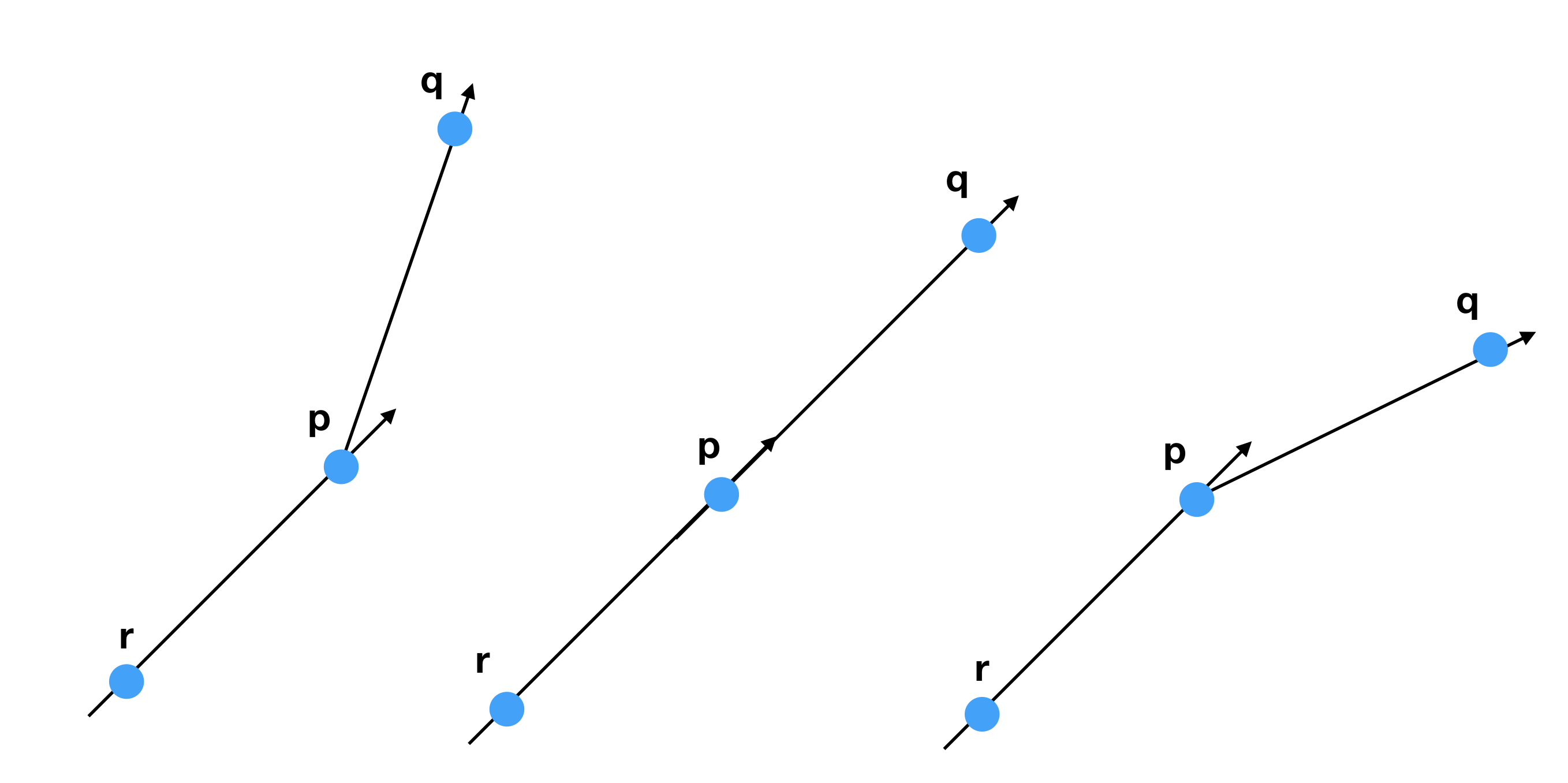
2. 벡터

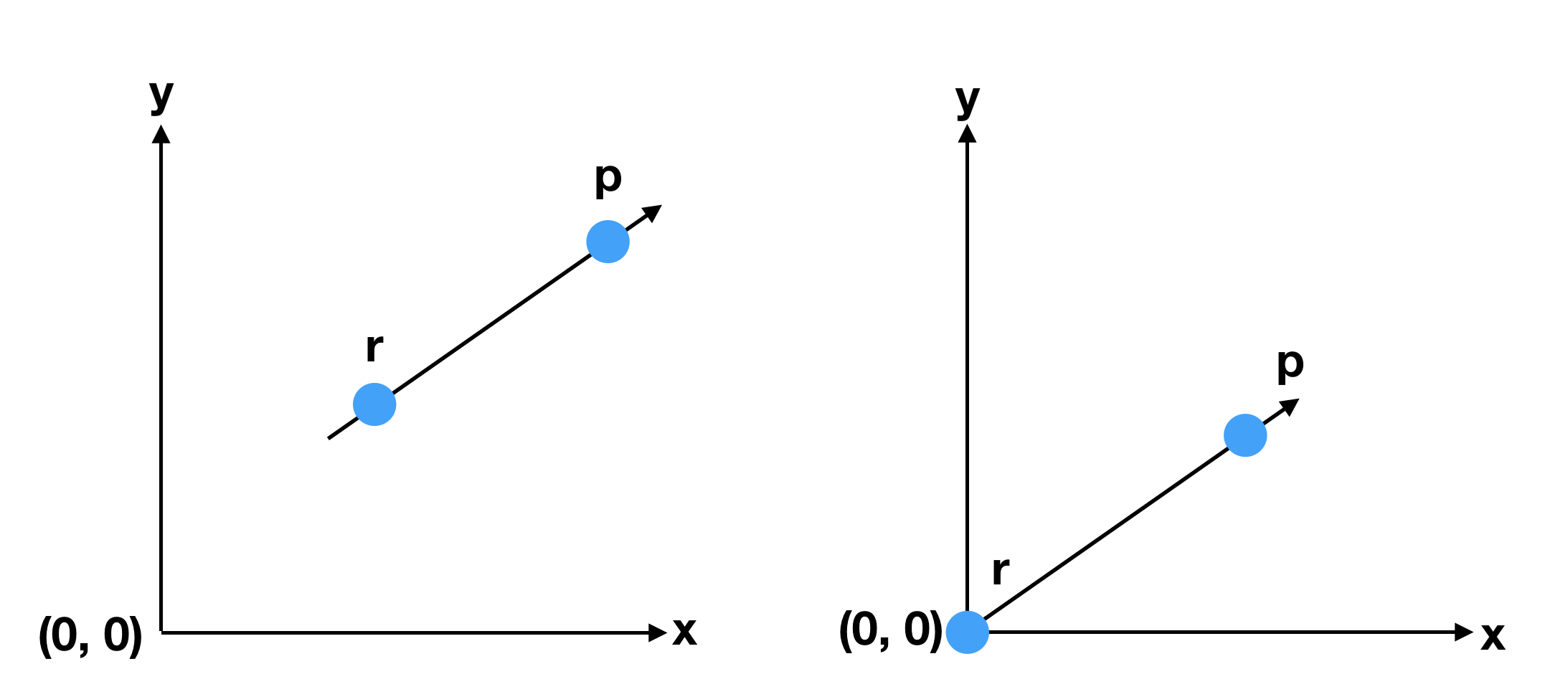
• 2차원 평면에서 벡터는 항상 원점에서 어느 점까지의 거리입니다.
• 두 개의 점이 있고, 시작점이 원점이 아닐때는 시작점을 원점으로 맞춰 벡터를 만듭니다.

3. 외적

• CCW 입니다.
• 외적 이란 두 벡터 사이의 곱연산입니다.
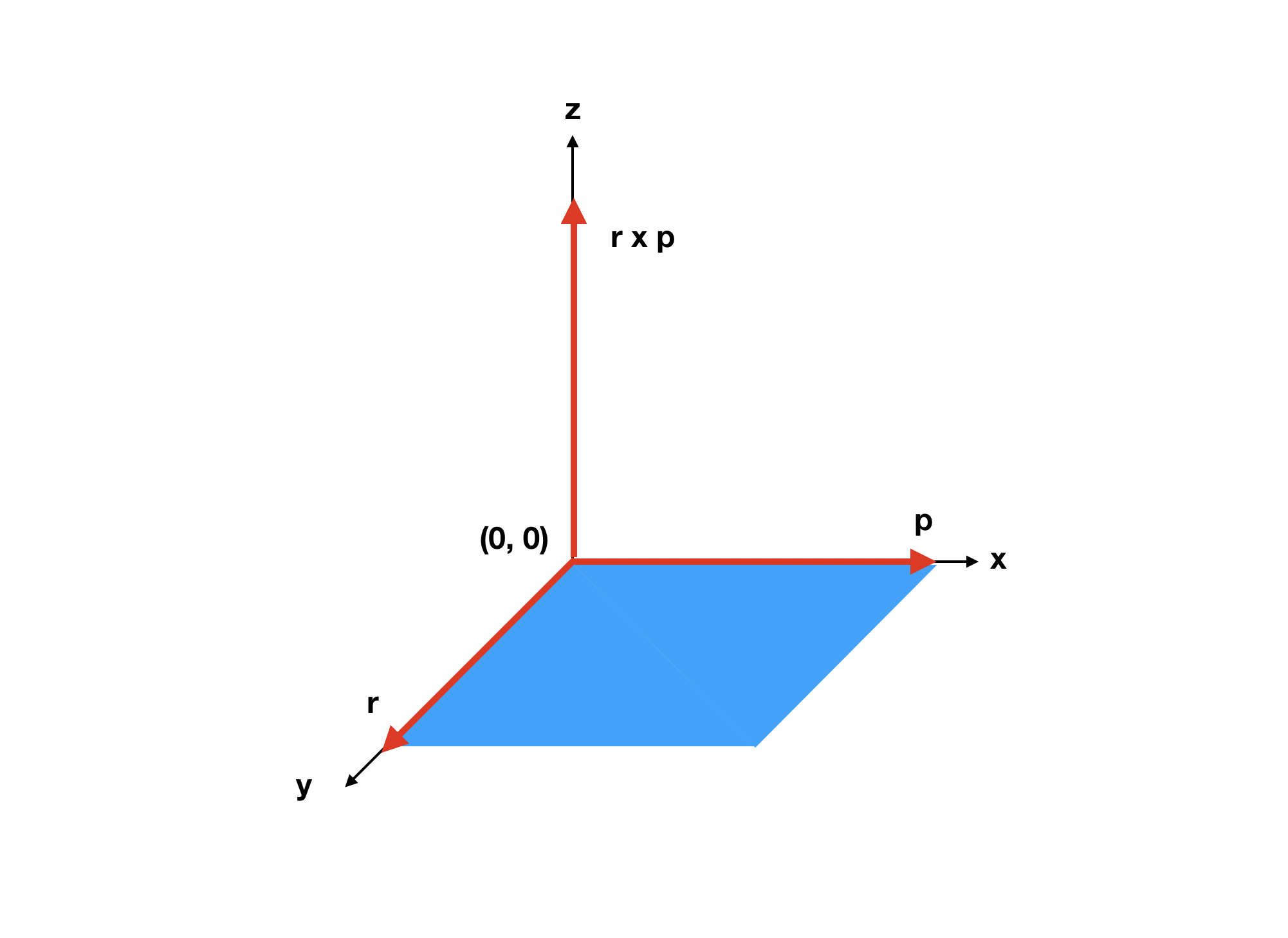
• 외적의 결과물은 두 벡터가 사이에 이루는 평행 사변형의 면적과 같습니다.
• 외적은 교환법칙이 성립하지 않습니다. AB 와 BA가 같지 않습니다.
• 오른손 법칙이 성립합니다. AB가 있을때 A벡터에서 시작해서 B벡터를 감쌓았을때 엄지손가락이 향하는 부호가 외적 결과물이 향하는 방향입니다.
• 면적을 구하기 때문에 헤론의 공식을 사용하기도 합니다만. 아래 방법을 추천합니다.
• 원점에서 시작하는 두벡터 r, p 가 있을때 외적을 계산하는 방법은 다음과 같습니다.

  r x p = r.x * p.y - r.y * p.x

4. 코딩

• 백준 온라인 저지 CCW 란 문제를 기준으로 작성하겠습니다.

#include <iostream>
#define lld long long int
using namespace std;

/*
 시간 복잡도: O(1)
 공간 복잡도: O(1)
 사용한 알고리즘: CCW
 사용한 자료구조: 배열
*/

int ccw_result;

// 점을 입력받을 구조체를 정의 합니다.
struct info{
    lld x, y;
};

// 정의한 구조체를 기반으로 배열을 생성합니다.(3개의 점이 주어집니다.)
info point[4];

// CCW
// 세점의 좌표정보를 순서대로 받습니다.
int ccw(info r, info p, info q){
    // 벡터의 외적을 수행합니다.
    // 점 p, q에대해 점 r의 x, y를 빼줘서 그래프를 원점에 맞춥니다.
    lld first = (p.x - r.x) * (q.y - r.y);
    lld second = (p.y - r.y) * (q.x - r.x);
    lld result = first - second;

    // 1) 1 이면 벡터rp 기준 점 q는 왼쪽에 존재합니다.
    if(result > 0) return 1;
    // 2) 0 이면 일직선에 존재
    else if(result == 0) return 0;
    // 3) -1 이면 벡터rp 기준 점 q는 오른쪽에 존재합니다.
    else return -1;
}

int main(){
    //1. 3개의 점을 순서대로 배열에 입력받습니다.
    for(int i=1; i<=3; i++){
        scanf("%lld %lld", &point[i].x, &point[i].y);
    }

    // 2. CCW를 수행합니다.
    ccw_result = ccw(point[1], point[2], point[3]);

    // 3. 결과 출력
    printf("%d\n", ccw_result);
}

5. 추천 문제

1. 백준 11758 CCW

• 바로 위에서 설명한 문제입니다.

2. 백준 2166 다각형의 면적

• CCW(즉, 벡터의 외적)은 평행사변형의 면적을 계산합니다.
• 평행사변형을 절반으로 나누면 삼각형의 면적이됩니다.
• 이를 사용해서 다각형의 면적을 구할 수 있습니다.

6. 소감

• 기하 알고리즘에 대해서, 저는 술담배는 해도 기하는 하지마라 라고 생각했습니다... 건강이 나빠지는 기분
• 가장 큰 이유는 낯설기 때문에
• 사실, 기하 알고리즘은 문제도 드물고, 레퍼런스도 드물고, 숫자도 너무 크고.. 등등
• 기하야 친구하자~